2024.3.30 - 4.5

Sat

ABC347

A. 直接模拟。
B. 暴力塞 set 即可，~~SAM模板~~。
C. 同时模 \(A+B\)，然后确认中间是否有一个隔断满足条件。
D. 分类讨论。
E. 前缀和与 set，差不多也是模板。
F. （补）发现可能的矩阵排布只有 \(6\) 种，分别计算左上、左下、右上、右下矩形最大值即可。
G. （未）最小割问题。

Sun

网络流材料

网络流理论篇

网络流应用篇

分配问题

\(n\) 个人分配 \(n\) 个工作，每个人分配一个工作，第 \(i\) 个人完成第 \(j\) 个工作的收益是 \(c_{i,j}\)，求最小总收益与最大总收益。

\(n\leq 100\)。

超源向所有工作连 \((1,0)\) 的边，表示该工作需要一个人且无收益。

所有人向超汇连 \((1,0)\) 的边，表示该人需要一个工作且无收益。

所有工作向所有人连 \((1,c_{i,j})\)，容量无所谓，表示把工作 \(i\) 安排给第 \(j\) 个人的总收益。

分别跑最小费用最大流与最大费用最大流。

运输问题

\(m\) 个仓库内的物品运送给 \(n\) 家门店，第 \(i\) 个仓库的储量是 \(a_i\)，第 \(i\) 个门店的需求是 \(b_i\)，保证储量总和等于门店需求总和，第 \(i\) 个仓库运送 \(1\) 单位物品给第 \(j\) 家门店的价格是 \(c_{i,j}\)，求运送所需的最小费用与最大费用。

基本等同于上一个问题，只不过把容量改一下即可。

老 C 的方块

【CQOI2017】

给定一个 \(R\times C\) 的矩阵，其中有一些位置有方块，删除它有代价，矩阵中有特殊边，如图中淡蓝色的为特殊边：

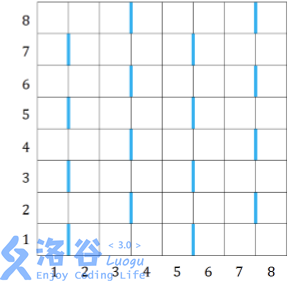
你需要删除最小代价的方块使得其中不存在如下形式的方格组合：

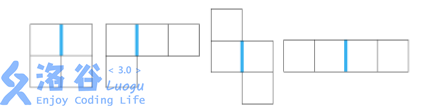
\(R,C,n\leq 10^5\)。

注：图片来自洛谷题解，本文仅限个人总结所用

如果我们将方格染色，则可以得到：

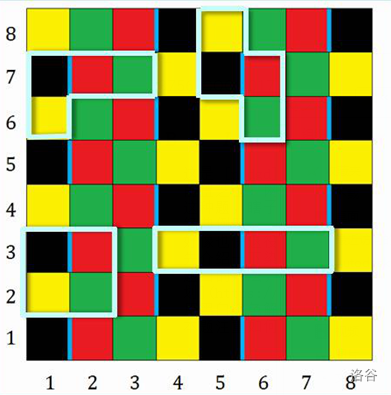
也就是说，考虑如下的方格：

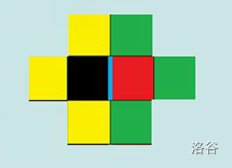
这四种颜色至少要丢一个。

不妨将超源连黄色，黄色连黑色，黑色连红色，红色连绿色，绿色连超汇，跑最小割即可，需要拆点。

水晶

【BJOI2016】

给定六边形密铺网格图，其中有些位置有水晶，考虑 \(120^{\circ}\) 坐标系三等分圆周，分别记为 \(x,y,z\) 轴，一个点的坐标向各方向走的步数（这意味着一个点有不同坐标），记 \(x+y+z\) 是 \(3\) 的倍数的点是特殊点，特殊点上的水晶的价值有 \(+10\%\) 的加成，你需要删除最少价值的水晶，满足：

不存在三个水晶，两两相邻排成三角形。
不存在三个水晶，两两相邻且共线，且中间位置的水晶处于特殊点。

\(n\leq 5\times 10^4\)。

坐标先处理成 \((x-z,y-z)\)，以下免去坐标方面的处理介绍。

类似上一题，将六边形网格图进行三色染色，黑色为特殊点，则两种情况如下：

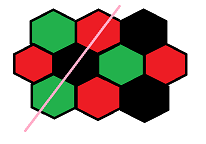
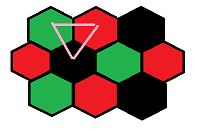
也就是说，对于一个黑色点而言，不能选择两种不同颜色的水晶保留。

超源连绿色，绿色连黑色，黑色连红色，红色连超汇，跑最小割即可，需要拆点。

Mon

负载平衡问题

Kaho 与 Suzune 邀请了一些朋友，总共 \(n\) 个人，第 \(i\) 个人分到了 \(a_i\) 块饼干，现在他们想要平均分配，每个人都可以往与自己相邻（环形座位）的人分 \(1\) 块饼干，问最少分的次数。

\(n\leq 100\)。

类比分配问题、运输问题做即可。

贪心+数学的解法可以做到 \(\mathcal{O}(n\log_2 n)\)。

上下界网络流

上下界网络流——算法学习笔记

上下界网络流——blog

Shoot the Bullet | 东方文花帖

【ZOJ3229】

射命丸文将要拍摄幻想乡内 \(m\) 名少女的照片，第 \(i\) 名少女至少要有 \(G_i\) 张，接下来的 \(n\) 天，每天可以拍摄不超过 \(D_i\) 张照片，以及你可以选择 \(C_i\) 位少女拍摄，对于你可以拍摄的某一位少女 \(T_{i,j}\) 而言，你可以拍摄 \([L_{i,j},R_{i,j}]\) 内任意非负整数张照片。

求最多拍摄的照片数量，或者告知无解。

\(m\leq 1000, n\leq 365\)。

以下记 \([l,r]\) 表示某条边的容量。

建立超源 \(S\) 与超汇 \(T\)，那么建模较为显然。

\(S\) 向所有少女连边，边的容量为 \([G_i, +\infty)\)。

所有天向 \(T\) 连边，边的容量为 \([0,D_i]\)。

每一天可供拍摄的少女 \(T_{i,j}\) 向每一天连边，边的容量为 \([L_{i,j},R_{i,j}]\)。

跑有源汇上下界最大流即可求出答案。

数字梯形

给定一个数字梯形，上窄下宽，从上端每一个点处往下找一条路径，每一步向左下或向右下，共计 \(m\) 条，在满足如下条件的情况下，最大化所经数字的和。

所经路径不交。
所经路径仅交于点。
所经路径允许有边重合。

\(n,m\leq 20\)。

显然在题设条件下，不交于点显然不交于边。

第一个条件，可以拆点，限制每一种条件。

第二个条件，可以直接连，仅把最后一行向超汇的容量开到正无穷。

第三个条件，可以直接连，仅把超源向第一行的容量设为 \(1\)。

跑最大费用最大流即可。

Tue

JOI 2024 Final

室温

\(n\) 个人，每个人的适宜温度是 \(a_i\)，每个人穿一件衣服使得自己的适宜温度降低 \(T\)，你可以设定空调，最小化每个人的适宜温度与空调温度的差的最大值。

\(n\leq 5\times 10^5, T\leq 10^9\)。

每个人的适宜温度都可以在模 \(T\) 意义下做，然后倍长，后半部分的适宜温度都要加上 \(T\)，然后求长度为 \(n\) 的所有连续区间的平均值作为适宜温度比较即可。

建设工程 2

\(n\) 座城市之间有 \(m\) 条无向通路，你需要选定一个点对并加修一条长度为 \(L\) 的通路，使得 \(S\to T\) 的最短距离为 \(K\)。

\(n,m\leq 2\times 10^5\)。

首先判掉已经符合条件的情况，然后记 \(f_i\) 表示 \(S\to i\) 的最短距离，\(g_i\) 表示 \(T\to i\) 的最短距离，则对于 \((u,v)\) 表示 \(f_u + L + g_v\leq K\)。

则枚举 \(u\)，计算的条件由不等式导出，直接二分即可。

马拉松比赛 2

给定 \(n\) 个球的位置 \(x_i\)，一条长度为 \(L\) 的路径，整点范围是 \([0,L]\)，有 \(Q\) 次询问，每一次询问给出 \(S,G,T\)，判断是否存在一种方式从 \(S\) 到 \(G\) 的方式使得：

拿到所有球，并在规定时间内到达，拿到 \(x\) 个球时的走一单位长度的时间是 \(x+1\)。

\(n,Q\leq 5\times 10^5, L,T\leq 5\times 10^5\)。

首先拿球一定是一段前缀与一段后缀，那么显然可以设 \(f_{l,r,0/1}\) 表示考虑了 \([1,l)\cup (r,n]\) 范围且当前在 \(l/r\) 位置时的最短时间，这基于 \(S\)。

不妨重新设计状态 \(f_{l,r,0/1}, g_{l,r,0/1}\) 表示先拿最左边/最右边的球到达当前状态的最短时间，初始状态为 \(f_{1,n,0} = g{1,n,1} = 0\)，此时不基于 \(S\)。

由于 \(T\leq 5\times 10^5\)，将位置去重，不超过 \(10^3\) 个位置，否则无解。

礼物交换

\(n\) 个人给出 \(q\) 次询问，每一次给出一段区间 \([l,r]\)，每个人携带了价值 \(a_i\) 的礼物，并希望拿到价值至少 \(b_i\) 的礼物，每个人不能给自己送礼，判断是否存在合适的送礼方式。

\(n,q\leq 5\times 10^5, b_i < a_i\)，且 \(a,b\) 共同构成一个 \(2n\) 的全排列。

按照 \(B\) 升序考虑，我们可以找到一种贪心策略：

对于第 \(i\) 个小朋友，找到 \(B_i\) 最大的，且可以接受第 \(i\) 个小朋友礼物的小朋友，把礼物给他。

那么，将 \([B_i,A_i]\) 视作区间，如果存在一个区间 \([B_i,A_i]\) 与其它区间不交，那么没有小朋友可以拿到他的礼物，此时将失败。

考虑求 \(L_i,R_i\) 表示左边、右边与之有交的区间编号，则一个询问不合法的要求是存在 \(i\) 使得 \(L_i < l\leq i\leq r < R_i\) 成立，扫描线即可。

Wed

线性基

参考资料

算法学习笔记

OI-Wiki

tzc_wkのblog

一种很新的构造方法

vector<ull> B;
void insert(ull x) {
    for (auto b : B)
        x = min(x, b ^ x);
    for (auto &b : B)
        b = min(b, b ^ x);
    if (x)
        B.push_back(x);
}

该种方法所构造的线性基，各元素的最高有效位各不相同，如果某个位是某元素的最高有效位，那么其它元素该位均为 \(0\)。

证明：采用归纳法。

显然，空集满足上述限制。

当插入 \(x\) 的时候，如果存在一个 \(b\in S\) 满足 \((b\oplus x) < x\)，那么 \(x\) 在该位上是 \(1\)，如果现在不异或，那么以后就无法消去该位上的 \(1\)。

最终可以得到的就是 \(x\) 与集合 \(S\) 内若干元素异或后可以得到的最小值，如果是 \(0\) 就说明可以被异或出来。

否则，\(x\) 一定有一个不同的最高有效位，插入后对 \(S\) 内所有元素进行该位消元，使得 \(S\) 依旧满足上述限制。

该方法可以有效解决异或最值与第 \(k\) 小问题，求最值异或时不能有初始值。

彩灯

【TJOI2008】
给定一整数集合 \(S\)，记 \(S\) 的所有子集可以得到的异或值集合为 \(T\)，求 \(T\) 的大小。

\(|S|\leq 50,V < 2^{50}\)。

线性基中任意个数的异或值所构成的集合，等于原序列中任意个数的异或值所构成的集合。

且线性基是极小的。

故线性基中不存在两个不同的子集使得两子集的异或值相同。

记线性基集合为 \(U\)，则方案数为 \(2^{|U|}\)。

元素

【BJOI2011】

各元素有权值 \(a_i\) 和价值 \(b_i\)，求一组元素的子集 \(S\)，使得该元素子集内有一子集 \(T\) 的元素权值异或为 \(0\)。

最大化选出元素的价值和。

\(n\leq 1000, V\leq 10^{18}\)。

线性基的大小一定保持不变，所以选出的元素的数量是一定的。

选出的元素必然构成线性基，于是往线性基里面插入的时候，插入成功则可选，否则不可选。

假设 \(x\) 没有成功插入，那么线性基中存在一子集 \(T\) 使得 \(T\) 内元素异或得到的结果是 \(x\)，随便拉出一个元素然后把 \(x\) 插进去也依旧构成线性基。

将元素按照价值降序，依次尝试加入线性基即可。

最大异或和

给定一整数集合 \(S\)，求一子集 \(T\subseteq S\)，使得 \(T\) 中元素异或最大。

\(n\leq 50, 0\leq V < 2^{50}\)

全部插入线性基，上述方法全部异或出来，贪心构造的则不断从高位往低位贪。

K小异或和

给定一整数集合 \(S\)，记 \(S\) 的所有子集可以得到的异或值的不可重集合为 \(T\)，求 \(T\) 中第 \(K\) 小。

\(|S|\leq 10^5, K\leq 10^{18}\)。

全部插入上述方法构造的线性基，排个序，然后如果 \(k\) 在某一位是 \(1\) 就直接异或对应元素。

如果线性基与原集合大小不同，则可以异或出 \(0\)，此时要先将 \(k\) 减去一。

albus就是要第一个出场

给定一整数集合 \(S\)，记 \(S\) 的所有子集可以得到的异或值的可重集合为 \(T\)，求 \(x\) 在 \(T\) 中第一次出现的排名。

\(|S|\leq 10^4\)。

结论：设线性基为 \(T\)，共计 \(2^{|T|}\) 种不同的异或值，各异或值出现 \(2^{|S|-|T|}\) 次。

证明：线性基中任意个数的异或值所构成的集合，等于原序列中任意个数的异或值所构成的集合。

我们可以等价的认为，\(|S|\) 是 \(|T|\) 加上 \(|S| - |T|\) 个 \(0\)，所以每一种元素的方案都是 \(2^{|S|-|T|}\) 次。

直接求出 \(x\) 的排名即可。

幸运数字

【SCOI2016】

给定一棵树，点有点权，多次询问树上一条路径上的点的点权构成的集合为 \(S\)，求一子集 \(T\subseteq S\)，使得 \(T\) 中元素异或最大。

\(n\leq 2\times 10^4, q\leq 2\times 10^5\)。

线性基的合并方式比较简单，把一个线性基里的元素插入到另一个线性基就可以了。

原题可以倍增加上线性基合并。

时间复杂度为 \(\mathcal{O}(q\log_2^3n)\)，可以过。

最大XOR路径

【WC2011】

求一条从 \(1\) 号点到 \(n\) 号点的路径，所经边的异或值最大，多次经过边则需要多次异或。

\(n\leq 5\times 10^4\)。

本题所称“环”为生成树上的一条非树边与树边所构成的环。

假设有一条从 \(1\) 号点到 \(n\) 号点的链，这个不一定优，但是我们可以选择经过一些环，而对于到环上的那一条路径的贡献呢？

链 -> 环 -> 链

贡献为 \(0\)，于是把环上的异或值插入线性基，随便找一条 \(1\to n\) 的路径然后找最大异或值即可。

Shortest Path Queries

给定一张 \(n\) 个点 \(m\) 条边的无向连通图，维护 \(q\) 个操作：

加边
删边
求两点间异或最短路。

\(n,m,q\leq 2\times 10^5, d\leq 10^9\)。

参考最长 XOR 路径，最终产生贡献的一定是 \(x\to y\) 的一条路径长度与一条非树边与树边组成的若干环。

于是采用线性基维护环的异或值，带权并查集维护树边的路径长度。

线段树分治维护加边删边即可。

最大割

给定一个图 \(G\)，记 \(G\) 中点集 \(V\)，求两个不交点集 \(S,T\) 满足 \(S\cup T = V\)，记割 \(C(S,T)\) 为所有满足 \(u(e)\in S, v(e)\in T\) 的 \(w(e)\) 的异或值，求最大割。

\(m\leq 500, V < 2^{500}\)。

权值以二进制形式给出

记 \(w_i\) 表示与 \(i\) 相邻的所有边的权值异或值，那么问题等价于求最大异或值，这是线性基可以做的。

位长过大？bitset！

目标：修改线性基内的元素。

我们再记插入元素时异或过 \(x\) 的元素的集合为 \(X(x)\)，把该元素本身也算进去！找出最小的 \(y\in X(x)\) 然后把线性基内所有元素异或上 \(y\)，如果要将 \(x\) 异或 \(w\)，则插入 \(y\oplus w\)。

相当于，原本插入异或 \(x\) 的元素变成了异或 \(x\oplus w\) 的，选择最小的 \(y\) 可以防止对后面元素产生影响，然后把 \(y\) 当作主元插入即可。

八纵八横

【HAOI2017】

给定一张连通图，加边，改加入的边的边权，删除加入的边，原边不动。

操作前、每一次操作后，求图中从 \(1\) 到 \(1\) 的一条路径，使得所经边异或值最大。

\(n,m\leq 500, Q\leq 1000, V < 2^{1000}\)。

参考最大XOR路径，即求所有环的异或最大值。

带一个带权并查集，加边、修改、删边都是好维护的。

最长 k 可重区间集

给定 \(n\) 个开区间，要求选出一些区间，使得不存在一个点被超过 \(k\) 个区间覆盖，求选出的区间的长度总和的最大值。

\(n\leq 500, k\leq 3\)。

问题转换一下：相交的区间属于不同的层，选出 \(k\) 层区间，要求选出的区间长度最大。

那么一个区间向另外一个区间连边的要求就是没有交。

首先限定流量为 \(k\)，各区间拆点并限制容量为 \(1\)，费用为长度的相反数（最大费用最大流，如果改变 SPFA 的话就不用）。

跑一遍流即可。

银行家

【SHOI2011】

有 \(n\) 个保险箱，第 \(i\) 个保险箱内有 \(a_i\) 个硬币，\(m\) 个人依次前来从自己所可以打开的一些箱子中拿走 \(b_j\) 个金币，每个人拿完金币后你可以调整打开的箱子中的金币的数量并关闭所有箱子。

求所有人将拿走的金币数量总和的最大值。

\(n\leq 600, m\leq 2500, a_i,b_i\leq 10^4\)。

如果有上一个人开箱子的话连上一个人即可完成“调整打开的箱子中的金币的数量”的要求。

Not Too Many Balls

【ABC332G】

给定 \(n+m\) 个点，超源 \(S\) 连接左部 \(n\) 个点，容量为 \(a_i\)，超汇 \(T\) 连接右部 \(m\) 个点，容量为 \(b_i\)，左部 \(i\) 号点连右部 \(j\) 号点的容量为 \(ij\)，求原图最大流。

\(n\leq 500, m\leq 5\times 10^5, 0\leq a_i,b_i\leq 10^{12}\)。

之前鸽了这题的 DP 写法，今天填坑。

让我们首先来列一下最小割的式子，然后做一下变换：

\[\begin{aligned} & \underset{P\subseteq L,Q\subseteq R}{\min} \{\underset{i\notin P}{\sum} A_i + \underset{j\notin Q}{\sum} B_j + \underset{i\in P}{\sum}\underset{j\in Q}{\sum} ij\} \\ =& \underset{P\subseteq L,Q\subseteq R}{\min} \{\underset{i\notin P}{\sum} A_i + \underset{j\notin Q}{\sum} B_j + \underset{i\in P}{\sum}i \underset{j\in Q}{\sum}j\} \\ =& \underset{0\leq S\leq \frac{n(n+1)}{2}}{\min} \{\underset{\underset{i\in P}{\sum} i = S}{\min} \{\underset{i\notin P}{\sum} A_i\} + \underset{j\notin Q}{\sum} B_j + \underset{j\in Q}{\sum}Sj\} \\ =& \underset{0\leq S\leq \frac{n(n+1)}{2}}{\min} \{\underset{\underset{i\in P}{\sum} i = S}{\min} \{\underset{i\notin P}{\sum} A_i\} + \underset{j\in R}{\sum}\min(Sj,B_j)\} \\ =& \underset{0\leq S\leq \frac{n(n+1)}{2}}{\min} \{\underset{i\in L}{\sum} A_i - \underset{\underset{i\in P}{\sum} i = S}{\max} \{\underset{i\in P}{\sum} A_i\} + \underset{j\in R}{\sum}\min(Sj,B_j)\} \\ =& \underset{0\leq S\leq \frac{n(n+1)}{2}}{\min} \{\underset{i\in L}{\sum} A_i -f_S + \underset{j\in R}{\sum}\min(Sj,B_j)\} \\ \end{aligned} \]

若 \(B_j\leq Sj\)，则有 \(\frac{B_j}{j}\leq S\)。

其中 \(f_S\) 可以在 \(\mathcal{O}(n^3)\) 内用背包 DP 求解，而后半部分可以先给 \(B\) 按照 \(\frac{B_j}{j}\) 排序然后双指针求解。

则时间复杂度为 \(\mathcal{O}(n^3 + m\log_2 m)\)。

Thur

最长 k 可重线段集

给定 \(n\) 个开线段，要求选出一些线段，使得不存在一条平行于 \(y\) 轴的直线穿过 \(k\) 条以上线段，求选出的线段的长度总和的最大值。

\(n\leq 500, k\leq 13\)。

问题基本等同于最长 k 可重区间集问题，对于 \(x\) 轴相同的线段稍微特判一下即可。

餐巾计划

\(n\) 天，每天需要 \(a_i\) 块干净餐巾。购买一块餐巾的价格是 \(P\)，慢洗店需要 \(M\) 天清洗一块餐巾，单价为 \(S\)，快洗店需要 \(N\) 天清洗一块餐巾，单价为 \(F\)，请问最少需要多少钱可以满足全部要求。

\(n\leq 2000\)。

我们需要区分干净餐巾和脏的餐巾。

根据我们的经验，这一天肯定要拆分成早上，晚上，每一天的晚上如果选择送去清洗则连向对应的早上。不送洗就连向次日晚上，购买就从源点连。

所有边均从晚上的点连出，为了满足网络流的“线性”，源点应当连向每一天的晚上，而汇点连早上。

如此，则表示晚上得到对应数量的脏餐巾，而白天得到干净的。

订货

【HAOI2010】

\(n\) 个月，第 \(i\) 个月的订货单价是 \(d_i\)，市场需求量为 \(u_i\)，有一个容量为 \(s\) 的仓库，单位物资在仓库里存储一个月的价格是 \(m\)，问最小成本，初始库存为 \(0\)。

\(n\leq 50\)。

简单题，每个月建一个点，建立源点 \(S\) 表示订购，汇点 \(T\) 表示售出，那么建图方式显然：

\[\begin{cases} S\to i: (+\infty, d_i) \\ i\to i+1: (s,m) \\ i\to T: (u_i,0)\\ \end{cases} \]

跑最小费用最大流即可。

网络扩容

【ZJOI2010】

给定一张网络，每条边有容量与扩容单位费用，问从 \(1\to n\) 的最大流与将最大流增加 \(k\) 的最小费用。

\(n\leq 10^3, m\leq 5\times 10^3\)。

最大流易求。

最小费用需要在参量网络上考虑，首先新开一个源点给出 \(k\) 的流量。

每条边再开一条费用为 \(w\)，容量无穷的边，原边的费用为 \(0\)，此时会尽量先流原图边，求出的为最小费用。

晨跑

【SDOI2009】

求一组 \(1\to n\) 的路径使得路径两两不交，路径数量最大的同时最小化路径长度总和。

\(n\leq 200, m\leq 2\times 10^4\)。

长度作为费用，除去 \(1,n\) 外的点拆点处理，则求最小费用最大流。

Fri

Almost Permutation

【CF863F】

给定 \(m\) 个条件，每一个条件形如【区间 \([l,r]\) 中的元素不大于/不小于 \(v\)】，求满足所有条件的长度为 \(n\)，值域为 \(n\) 的数列中，最小的所有数字出现次数的平方和。

\(n\leq 50,m\leq 100\)。

首先可以求出每个元素的取值范围，然后对数字拆点（一个数字只能选择一个值），对值也拆点，方便计算贡献。

然后对值的入点和出点，差分掉平方和，将差分后的结果作为费用。由于 \(f(x)=x^2\) 二阶导大于 \(0\)，所以差分结果单调递增，最小费用会先保证流经费用最少者，恰好可以还原出“平方”。

工作安排

【SDOI2011】

\(n\) 种物品 \(m\) 个人，物品有需求量 \(C_i\)，每个人可以做指定的物品，每个人做一定数量的物品所得的愤怒值是一个分段函数。

满足后段单个物品的愤怒值大于前段，求搞定需求量的最少愤怒值。

\(n,m\leq 250\)。

首先你可以选择按照上一题的方式拆点，但是会发现不需要拆点，源点连零件，零件连可用的人，人连汇点，连段数 \(+1\) 条边，分别表示每一段的物品总数与单个物品的愤怒值即可。

球队收益

【JSOI2009】

\(n\) 个球队，第 \(i\) 个球队的最终收益是 \(C_i\times w_i^2 + D_i\times l_i^2\)，其中 \(w_i,l_i\) 表示该球队赢的次数与输的次数。

每个球队已经赢了 \(a_i\) 场，输了 \(b_i\) 场，接下来有 \(m\) 场比赛，第 \(i\) 场比赛的参赛选手是队伍 \(u_i,v_i\)。

求所有球队的总收益的最小值。

\(n\leq 5000, m\leq 1000, D_i\leq C_i\)。

考虑差分，假设初始情况队伍全部输掉，每一场比赛会使一个队伍赢的次数 \(+1\) 同时输的次数 \(-1\)，带来的收益是：

\[C_i(x+1)^2 + D_i(y-1)^2 - (C_ix^2+D_iy^2) = 2C_ix-2D_iy + C_i + D_i \]

随着赢的次数增加，输的次数减少，该式子将递增。

把上述式子作为费用，加上之后的比赛队伍全部输掉的收益即为最小总收益。

软件开发

【HNOI2001】

\(n\) 天，每天需要 \(a_i\) 块消毒毛巾。购买一块消毒餐巾的价格是 \(f\)，慢洗店需要 \(a\) 天消毒一块毛巾，单价为 \(f_a\)，快洗店需要 \(b\) 天消毒一块毛巾，单价为 \(f_b\)，请问最少需要多少钱可以满足全部要求。

\(n\leq 1000\)。

同餐巾计划问题。

注意本题第 \(i\) 天送洗需要在第 \(i + d + 1\) 天取回，而非第 \(i + d\) 天，其中 \(d\) 是消毒时间。

方格取数加强版

给定一个 \(n\times n\) 的矩阵，找出 \(K\) 条从 \((1,1)\) 到 \((n,n)\) 的路径，只能向右或向下，使得路径经过的数字的权值和最大。

多次经过同一个格子只计算一次权值。

\(n\leq 50, K\leq 10\)。

拆点，每个点间连接两条边 \((1,y)\) 与 \((+\infty,0)\)，这可以表示出只计算一次权值。

再限制流量为 \(K\) 即可。

最小路径覆盖问题

给定一个 DAG，求该图的最小路径覆盖。

假设每条路径都只覆盖一个点，那么需要 \(n\) 条路径。

每将两条路径首尾相连，那么答案减一。

通过最大流可以求出最多合并的路径数量。

星际竞速

【SDOI2010】

从起点 \(0\) 开始，从任意一点到点 \(i\) 的时间是 \(A_i\)，有 \(m\) 条有向边可以使用。

求经过每个点恰好各一次的最短时间。

\(n\leq 800\)。

这个问题可以转化为：【每个人从起点出发到达终点，中途只能通过 \(m\) 条有向边，要求最小化经过每个点恰好各一次的最短时间】

这个问题很显然是最小路径覆盖问题。

至于 \(A_i\)，可以从源点向每个点的入点连边，表示可以新建一个人，继续完成目标。

拯救皮卡丘

【ZJOI2011】

给定一张图，点编号为 \(0\sim n\)，有 \(K\) 个可以独立行走的人，初始都在 \(0\) 号点，要求编号为 \(1\sim n\) 号点需要按顺序通过，每个点被通过仅当有至少一个人到达，求最短同行时间。

\(n\leq 150\)。

首先用 Floyd 求出 \(i\to j\) 的不经过编号大于 \(\max(i,j)\) 的点的最短距离，记为 \(f_{i,j}\)。

然后可以生成一个 \(n\) 个点的完全图，从编号小的点到达编号大的点。

接下来转为最小路径覆盖，两点间的边权为 \(f_{i,j}\)。

posted @ 2024-03-31 08:13 ydzr00000 阅读(85) 评论(0) 收藏举报

刷新页面返回顶部

ydzr00000