1.2半导体二极管

 

1.2  半导体二极管

造型4，交流通过时，产生磁场，磁场与磁场间产生电应力（电应力大使螺丝松开）

1.2.1  常见结构

集成的概念：同一硅片上敷多个PN结（扩散工艺），封装后大小相同

 

 

1.2.2  二级管的伏安特性

一、伏安特性

二极管比PN结多了两边的P区和N区，有体电阻

1、体电阻的存在，（相同电压下）电流比PN结小

2、反向电流大一些

即曲线左边较PN结特性往下些，另一边往右些

 

 

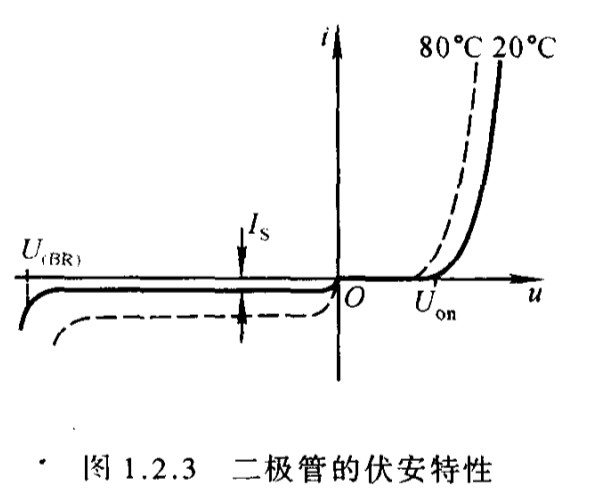
二、温度的影响

1、T↑，正向←，反向↓

正向： T↑，粒子活性↑（本征激发），即U相同时，I大

反向：T↑，少子影响明显，反向饱和电流下移

2、室温，1℃↑，正向压降2-2.5mv↓

10℃↑，反向电流增大一倍

各部分特性如何使用

整流：单向导电性可用于规定电流方向，将交流变成直流；

钳制电位：U_on后，电压变化很小，硅管工作区间0.6~0.8V，取0.7V，误差上下不超过0.1。可近似认为正向导通时，电压不变

温度传感器：温度对反向饱和电流的影响（廉价）

以二极管作为温度传感器的电子体温计：二极管后面跟电桥，做个压频转换，频率出来后，用定时器、单片机，再拿个显示器。十块钱之内做完

反向击穿区可做稳压二极管（与正向稳压不同在于，正向是死的0.7，反向电压可改变）

1.2.3  二级管的主要参数

一、最大整流电流I_F

二极管长期工作时所能通过的正向平均电流的最大值

 

二、最高反向工作电压U_R

UR为击穿电压U_（BR）的一半，有一定的超载能力

 

三、反向电流I_R

I_R越小，反向截止特性越好

 

四、最高工作频率f_M

势垒电容和扩散电容构成二极管的结电容，容抗公式Xc = 1/（ωC）= 1/（2πfC）。f上升到一定程度，近似导通，二极管此时不通过PN结而是在等效的结电容上电流来回流通，此时二极管的单向导电性被破坏

---

 

分析二极管是什么样的电阻

 

非线性（线性电阻是经过原点的一根直线）

如何分析含非线性电阻的电路

图解法，根据特性曲线与外电路所给的负载线，算出交点即工作点

上面的方法计算太麻烦，我们往往把这种非线性元件用线性元件表述出来，这种电路称为等效电路

---

 

1.2.4  二极管的等效电路

一、等效电路

模型1：在一定条件下，它们的外特性（电压与电流的输出关系）等效

模型2：根据物理原理等效

 

二、伏安特性折线化

 

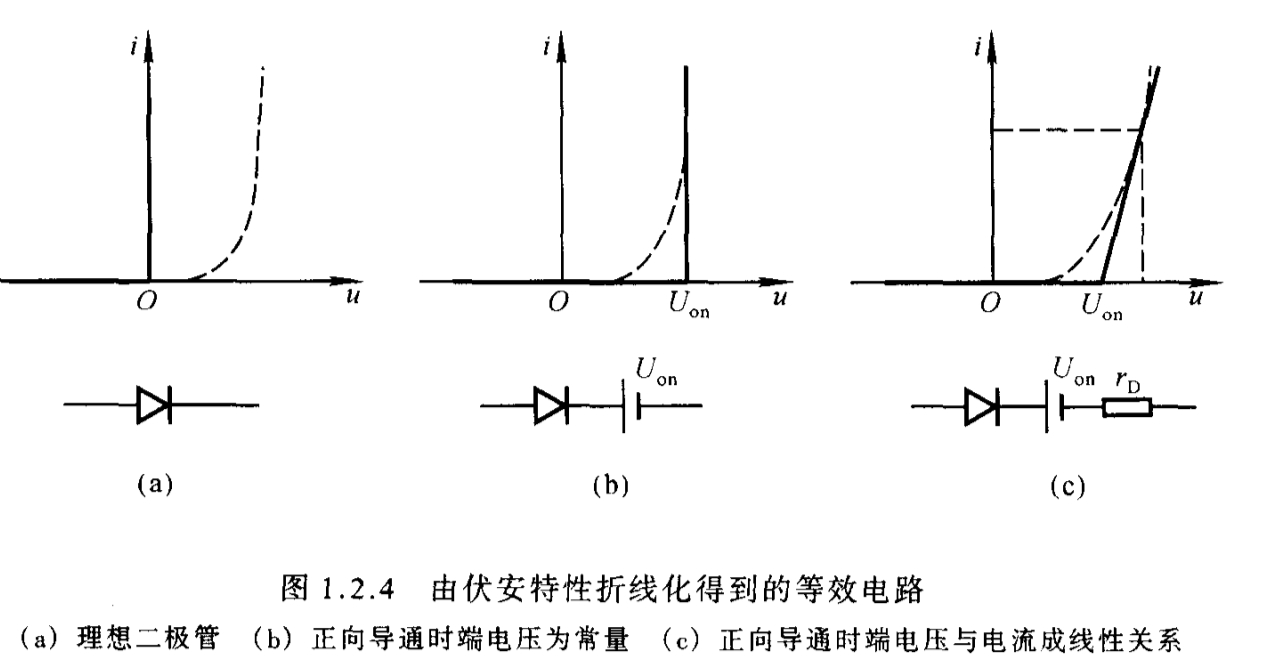
a  理想二极管：折线在坐标轴上，读出来的意思即为二极管严格遵循单向导电性，一旦P>N，马上正向导通，且导通电降为0；一旦反向，一点反向电流都没有

 理想二极管符号中间直线断开

b  有开通电压，本书后面认为当PN间电压大于导通电压，二极管导通，导通后维持电压不变（计算中硅管0.6~0.8取0.7V，误差0.1V相对于十几伏的电源可忽略。实际中，二极管电压变化必然引起电流变化，即满足伏安特性曲线）

c  由图画等效电路

 

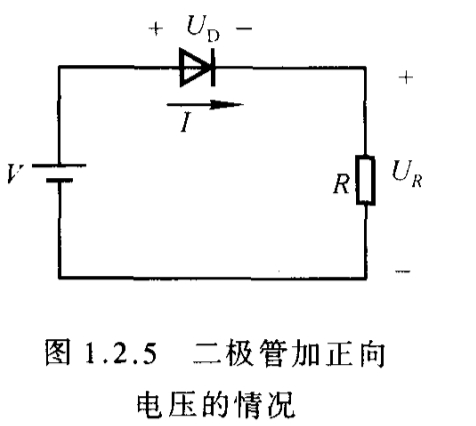
对模型a，有I=V/R

对模型b，有I=（V-Uon）/R，再严谨需要先比较V与U_on

---

 

画出U_o波形（对应模型b）

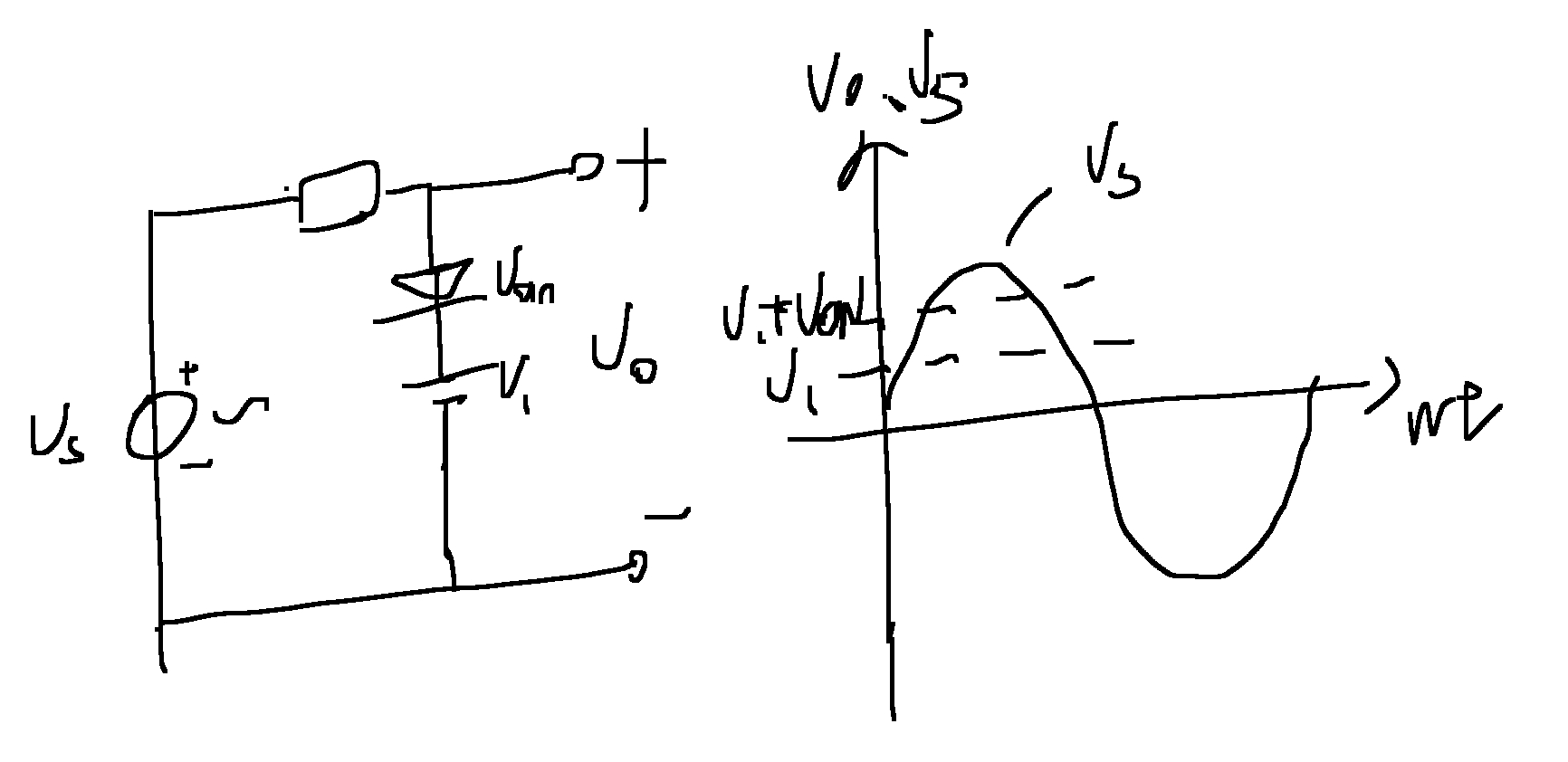
分析

二极管截止时，U_o=U_s

二极管导通时，U_o=U₁+U_on

先假设二极管截至看符不符合条件，设二极管和直流电源间电位为U₁

则二极管两端电压U_s-U_1≤U_on时截止

U_s-U₁>U_on时导通，导通后输出电压=U₁+U_on

将顶部削平，限幅电路（用了二极管的两个特性，单向导电性，导通后导通电压视为不变）

---

 

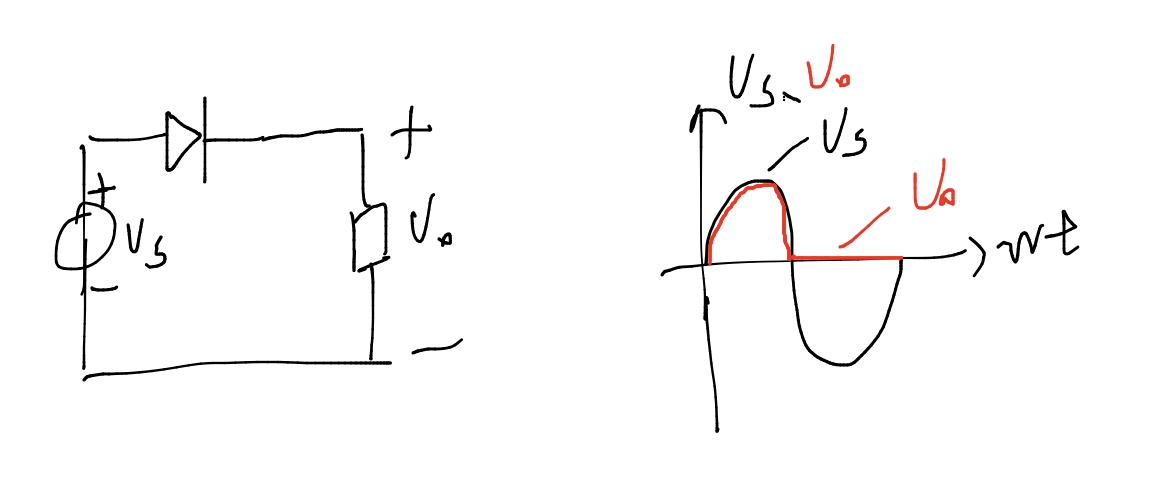
模型a，理想二极管（中间直线断开），当U_s>0时导通，U_s<0时截止

该过程称为整流

 

三、二极管的微变等效

1、直流→I_D=（V－u_D）/R

2、r_d=U_T/I_D，用电阻取代二极管去分析电路

 

i_d=U_i/(r_d+R)

i_D=i_d+I_D（交流分量+直流分量）

 

 

 

1.2.5  稳压二极管

 一、特点：

小于6V主要工作在齐纳击穿，大于6V主要工作在雪崩击穿

 

二、伏安特性

稳压二极管本质上还是二极管，正向导通，反向没到击穿区前截止

 

双向稳压二极管：相当于两个二级管背靠背接在一起

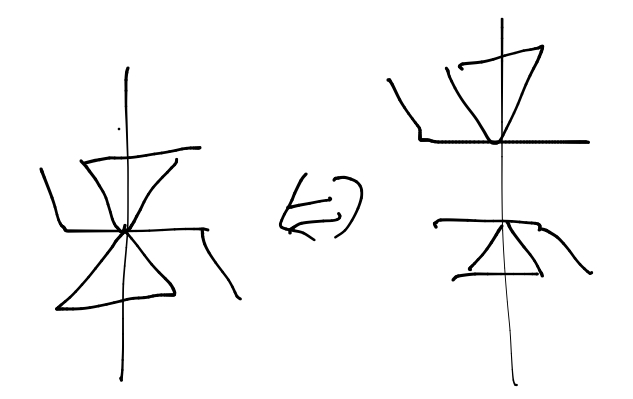
①都截止②一个导通一个反向击穿

 

三、主要参数

温度越高齐纳击穿越容易

因此小于4V时，α是负温度系数

大于7V雪崩击穿，α是正温度系数（见上节内容）

 

对于含稳压二级管的电路

全局观：先设稳压二极管未击穿，求其并联支路两端的电压判断是否击穿，再算电流（稳压二极管并联负载电阻导致与前端电阻分压变小）

二级管使用必须考虑限流电阻（才能满足伏安特性曲性，电压上升必然导致电流上升，因为限流电阻分压，管子两端电压才只变化一点点）