1

B.Ball Dropping

 

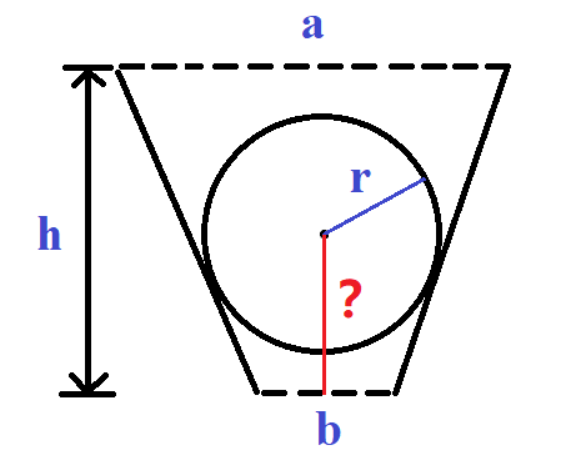
题意：

给定一个等腰梯形的上底a，下底b和高h和一个球的半径r，问这个球回不回被卡在梯形里，如果会，算出卡住时球心距离下底的距离

思路：

这题可以用相似做，也可以建系，

说下建系的方法：

 

 

 

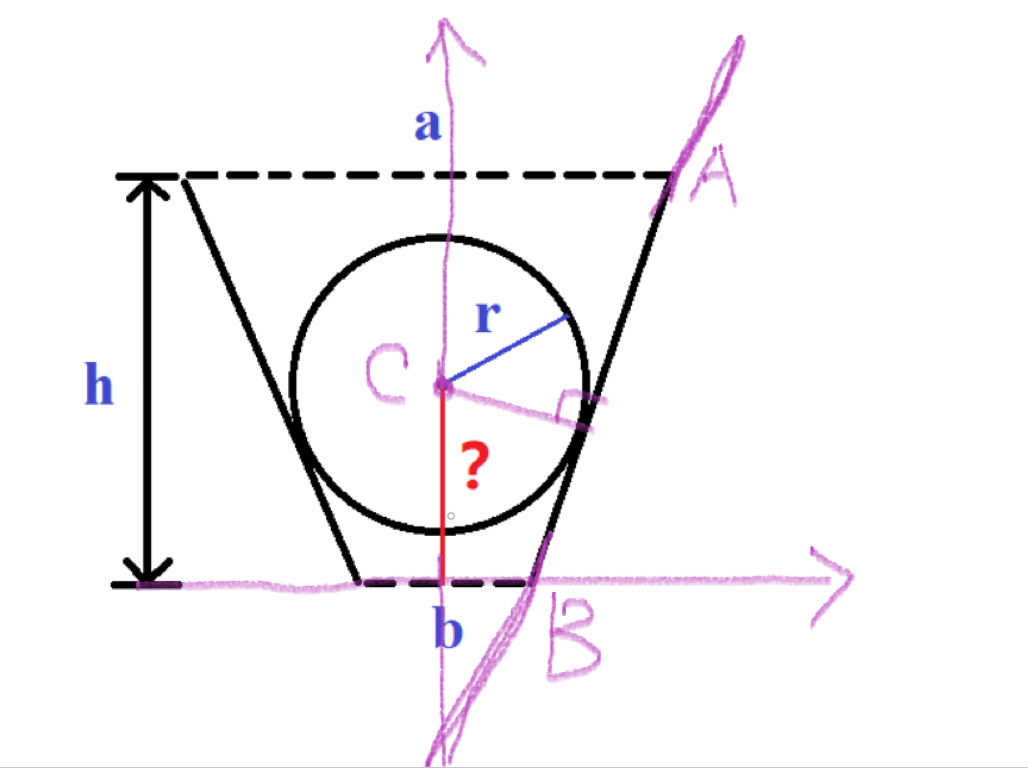
A的坐标是(a / 2, h), B的坐标是(b / 2, 0), C的坐标是(0，h)，现在知道C到AB的距离r，可以求出d

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

int main(){
    double r, a, b, h;
    cin >> r >> a >> b >> h;
    double k = h / ((a - b) / 2);
    double d = sqrt(1 + k * k) * r - k * b / 2;
    if(2 * r <= b) cout << "Drop" << endl;
    else
    {
        cout << "Stuck" << endl;
        printf("%.10lf", d);
    }
    return 0;
}

F.Find 3-friendly Integers

题意：

给两个数L和R，求出其中满足条件：%3 == 0或包含%3 == 0的数的数的总数

思路：

先分析下找下规律，因为这个题L和R数据范围是10^18,所以硬干就肯定不行。

然后，这个题的规律就是100以后的数都是满足条件的，比如101就是有0,102 % 3 == 0，116包含6.。。。。。

所以对于100以下的数，我们枚举所有数，100以上的数就R - 100 + 1或R - L + 1

 

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

int main()
{
    int T;
    cin >> T;
    while (T -- )
    {
        LL l, r;
        cin >> l >> r;
        LL cnt = 0;
        if (l < 100)
        {
            for (int i = l; i < 100 && i <= r; i++)
                if (i % 3 == 0) cnt++;
                else
                {
                    int tmp = i;
                    while (tmp)
                    {
                        if (tmp % 10 % 3 == 0) cnt++;
                        tmp /= 10;
                    }
                }

            if (r >= 100) cnt += r - 100 + 1;
        }
        else if (l >= 100 && r >= 100) cnt = r - l + 1;

        cout << cnt << endl;
    }
    return 0;
}