第十一届蓝桥杯省赛B组

 

 

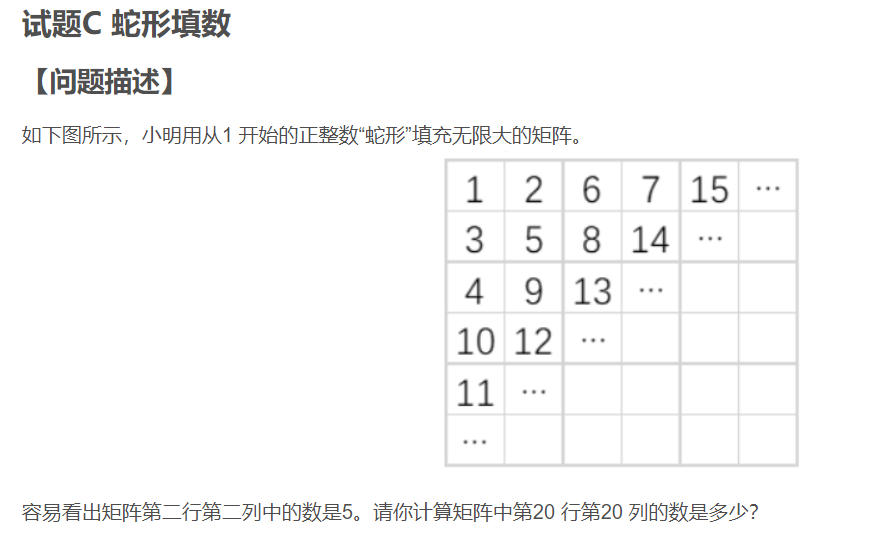
这道题是一道填空题，然后我们可以通过观察找规律来得出答案
通过观察发现：
第一行第一列 ： 1 1^2 + (1-1)^2 = 1
第二行第二列： 5 2^2 + (2-1)^2 = 5
第三行第三列： 13 3^2 + (3-1)^2 = 13
第四行第四列： 25 4^2 + (4-1)^2 = 25
第五行第五列： 41 5^2 + (5-1)^2 = 41

所以通过找规律发现：第n行第n列 = n^2 + (n-1)^2
第二十行第二十列 ： 20*2 + (20-1)^2 = 761

答案：761

接下来两个日期题：

 

 

解题思路：

1.用 0 ~ 6 来代表 周一 至 周日；
2.用 sum 来代表 2000年1月1日 至 某年某月某日 所经过的天数；
3.由于 2000年1月1日 是周六，那么用 (sum + 5) % 7 就能表示 某年某月某日 是星期几；
4.因为 2020年10月1日 未处理，所以最后 ans += 2

#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>

using namespace std;

typedef long long LL;
typedef pair<int, int>PII;

int days[] = { 0 , 31 , 28 , 31 ,30 ,31 , 30 , 31 ,31 , 30 , 31 , 30 , 31 };

bool leap(int year)
{
    if ((year % 4 == 0 && year % 100 != 0) || year % 400 == 0) return true;
    return false;
}

int getday(int year, int month)
{
    if (month == 2) return 28 + leap(year);
    return days[month];
}

int main()
{
    int sum = 0, ans = 0;
    for (int i = 2000; i <= 2019; i++)
        for (int j = 1; j <= 12; j++)
            for (int k = 1; k <= getday(i, j); k++)//这个月第几天，看是不是月初
            {
                int weekday = (sum + 5) % 7;
                if (k == 1 || weekday == 0) ans += 2;
                else ans++;

                sum++;
            }

    //单独处理2020年
    for (int j = 1; j <= 9; j++)
        for (int k = 1; k <= getday(2020, j); k++)
        {
            int weekday = (sum + 5) % 7;
            if (k == 1 || weekday == 0) ans += 2;
            else ans++;

            sum++;
        }

    cout << ans + 2 << endl;
    return 0;
}

 

 

 

 

解题思路：

直接枚举年份 a，将其翻转得到 b，那么 a + b 就是一个回文数；
用 substr 分离出月份和天数，再判断月份和天数是否合法；

实用函数：

stoi(x)：将字符串转换成数字；
to_string(x)：将数字转换成字符串；
substr(u, len)：从第 u 位开始，截取一段长度为 len 的字符串；

写的前三个有关日期天数的函数还是很好用的

#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>

using namespace std;

typedef long long LL;
typedef pair<int, int>PII;

int days[] = { 0 , 31 , 28 , 31 ,30 ,31 , 30 , 31 ,31 , 30 , 31 , 30 , 31 };

bool leap(int year)
{
    if ((year % 4 == 0 && year % 100 != 0) || year % 400 == 0) return true;
    return false;
}

int getday(int year, int month)
{
    if (month == 2) return 28 + leap(year);
    return days[month];
}

int main()
{
    string  res1 , res2;
    int n;
    cin >> n;

    bool flag1 = false, flag2 = false;
    for (int i = n / 10000; i <= 9999; i++)
    {
        string a;
        a = to_string(i);
        string b;
        b = a;

        reverse(b.begin(), b.end());
        if (stoi(a + b) == n) continue;

        int month = stoi(b.substr(0, 2));
        int day = stoi(b.substr(2, 2));

        if (month < 1 || month > 12) continue;
        if (day < 1 || day > getday(i, month)) continue;

        //ABAB型为月份和日期相同
        string s1 = a.substr(0, 2);//月份
        string s2 = a.substr(2, 2);//天数

        if (!flag1)//回文
        {
            res1 = a + b;
            flag1 = true;
        }
        if (!flag2 && s1 == s2 && s1[0] != s1[1])//ABAB型  A!=B
        {
            res2 = a + b;
            flag2 = true;
        }

        if (flag1 && flag2) break;
    }

    cout << res1 << endl << res2 << endl;

    return 0;
}

 

 

 

 

用set

在同一个平面内，如果添加的每一条直线互不相交，则每添加一条直线，就会增加一个平面；当添加一条直线时，这条直线与当前平面内已有直线每产生一个不同位置的交点时，这条直线对平面总数量的贡献会额外增多一个， 记为Si，值Si的值为经过该直线的点+1，1为直线自身贡献的平面 ， 结果为每一条直线的贡献加上最开始的一个平面，既：S1到Sk的和（k为所有不重合直线的数量）再加上1。
所以我们可以在每添加一条直线时设置一个空的set,将直线与当前平面内其他直线的交点的xy坐标存入set中，如果这一条直线不是重边，则这条直线的贡献为set.size()+1，即ans为所有直线的贡献加上原来的一个平面。

#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <set>

using namespace std;

typedef long long LL;
typedef pair<int, int>PII;

double L[1010][2];
bool st[1010];

pair<double, double>p;
set<pair<double, double>>points;

int main()
{
    int n;
    cin >> n;
    LL res = 0;
    for (int i = 0; i < n; i++)
    {
        cin >> L[i][0] >> L[i][1];
        for (int j = 0; j < i; j++)//依次比较 查找重边
        {
            if (st[j]) continue;//直线是重边

            if (L[i][0] == L[j][0])//斜率相等，判断平行还是重合
            {
                if (L[i][1] == L[j][1])
                {
                    st[i] = true;
                    break;
                }
                else continue;//平行，不需要计算交点
            }

            p.first = (L[j][1] - L[i][1]) / (L[i][0] - L[j][0]);//交点x的坐标
            p.second = L[i][0] * p.first + L[i][1];//交点y的坐标
            points.insert(p);
        }

        if (!st[i]) res += points.size() + 1;//若当前点不是重边，更新答案
    }
    
    cout << res + 1 << endl;

    return 0;
}