实用指南：Day25_【深度学习（4）—自动微分模块】

一、回顾

        线性回归的目的是找到最佳的拟合线，而这个最佳是由损失函数定义的，优化这个过程就是最小化损失函数，优化损失函数的方法有正规方程法和梯度下降法，随着模型越来越复杂，一般都是使用梯度下降。而梯度下降也有实现方式——自动微分，就是pytorch框架在梯度下降的一种实现方式。

也就是说，PyTorch中，我们使用自动微分模块：自动计算神经网络中损失函数对模型参数的梯度，从而实现反向传播和参数更新。就是用到一个方法：backward()

二、介绍

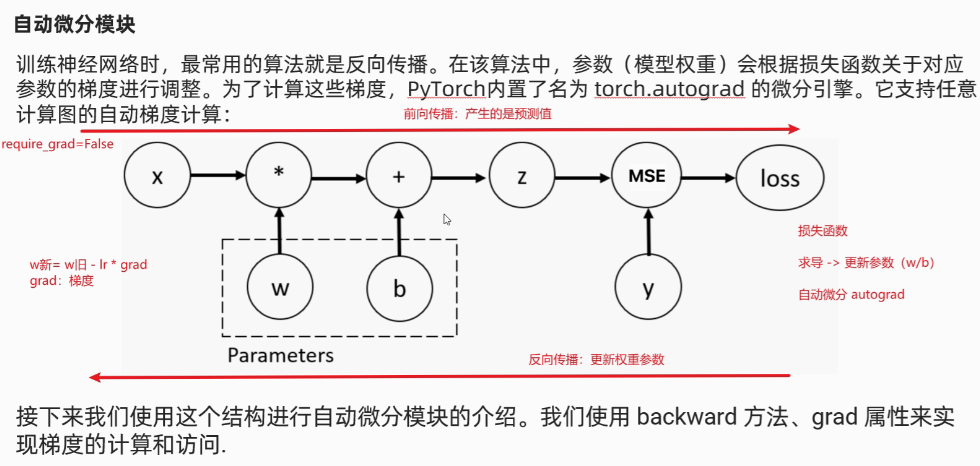
• 正向传播：结果是损失函数
• 反向传播：结果是参数w、b

三、模板

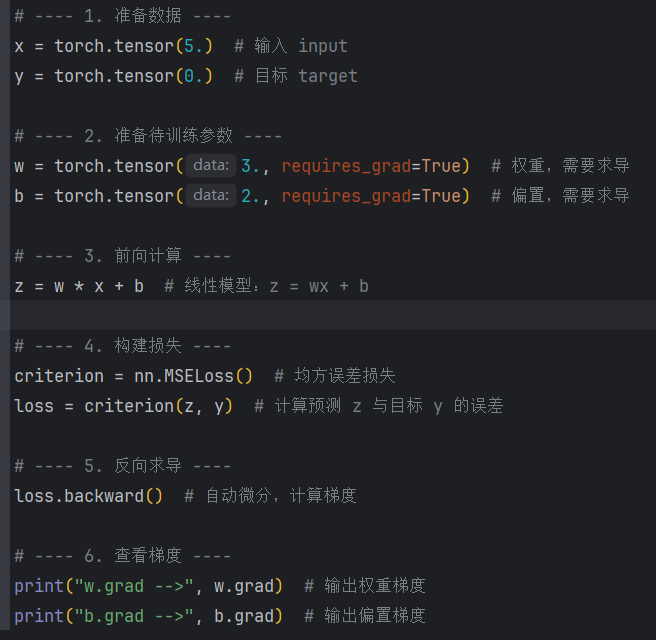
需要计算梯度的张量需要设置 requires_grad=True 属性

四、案例

案例1—— 单个参数w、b

def demo01():
# 准备x、w、b、z
x = torch.tensor(3.)
w = torch.tensor(2., requires_grad=True)
b = torch.tensor(1., requires_grad=True)
z = w * x + b
# 准备y
y = torch.tensor(0.)
# w:(x * w + b - y)^2 = 2(x * w + b - y)*x = 2(2*3+1)*3 = 14*3 = 42
# b:(x * w + b - y)^2 = 2(x * w + b - y)*1 = 2(2*3+1)*1 = 14*1 = 14
# 计算损失
criterion = nn.MSELoss()
loss = criterion(z, y)
# 使用自动微分模块计算梯度
loss.backward()
# 查看梯度结果
print('w-->', w.grad)
print('b-->', b.grad)
if __name__ == '__main__':
demo01()

案例2——多个参数w、b

def demo02():
# 准备x、w、b、z
x = torch.randn(2, 3)
w = torch.randn(3, 5, requires_grad=True)
b = torch.randn(5, requires_grad=True) # 广播机制：(1,5) -> (2,5)，实现和y的相加
z = torch.matmul(x, w) + b
# 准备y
y = torch.randn(2, 5)
# 计算损失
criterion = nn.MSELoss()
loss = criterion(z, y)
# 使用自动微分模块计算梯度
loss.backward()
# 查看梯度结果
print('w-->', w.grad)
print('b-->', b.grad)
if __name__ == '__main__':
demo02()

                ​