第五节:二叉树相关(反转二叉树[递归/栈]、最大路径和)
一. 反转二叉树
一. 题目描述
给你一棵二叉树的根节点 root ,反转这棵二叉树,并返回其根节点。
示例:
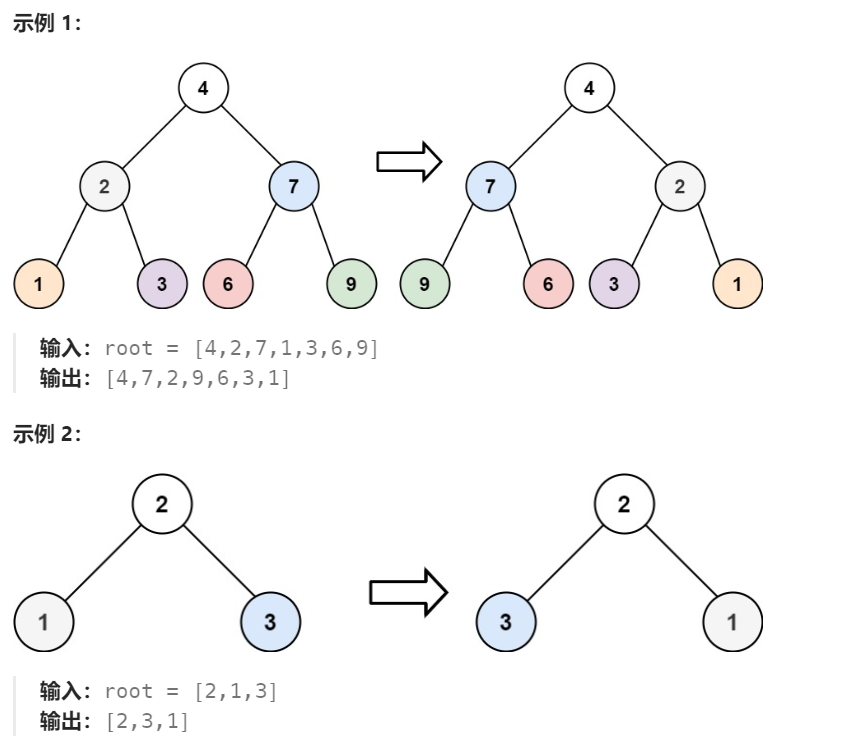
leetcode:https://leetcode.cn/problems/invert-binary-tree/description/
难度:【简单】
二. 思路分析1-递归
1. 首先要有递归结束的条件
2. 先写出来第一次运行的代码,然后将相应的位置改为递归调用即可
class TreeNode {
val: number;
left: TreeNode | null;
right: TreeNode | null;
constructor(val: number, left?: TreeNode | null, right?: TreeNode | null) {
this.val = val === undefined ? 0 : val;
this.left = left === undefined ? null : left;
this.right = right === undefined ? null : right;
}
}
function invertTree(root: TreeNode | null): TreeNode | null {
//非空判断
if (root === null) return null;
//第一次代码
// let leftNode = root.left;
// root.left = root.right;
// root.right = leftNode;
//递归反转
let leftNode = root.left;
root.left = invertTree(root.right);
root.right = invertTree(leftNode);
return root;
}
三. 思路分析-栈
1. 声明栈,默认root入栈
2. while循环,栈中有数据
A. 出栈,左右子节点交换(都为null,不操作)
C. 左右子节点不为null,则入栈
function invertTree(root: TreeNode | null): TreeNode | null {
//1.非空判断
if (root === null) return null;
//2.声明栈结构(数组模拟)
let stack = [root];
//3.遍历栈结构,进行反转交换
while (stack.length > 0) {
//3.1 出栈
let current = stack.pop()!;
//3.2 左右子节点交换位置
//左右都为null, 不进行任何操作 (相当于null null 不需要进行交换,一个优化点)
if (current.left !== null || current.right !== null) {
let temp = current.left;
current.left = current.right;
current.right = temp;
}
//3.3 继续将节点入栈
if (current.left) stack.push(current.left);
if (current.right) stack.push(current.right);
}
return root;
}
二. 最大路径和
一. 题目描述
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和:是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和
示例:
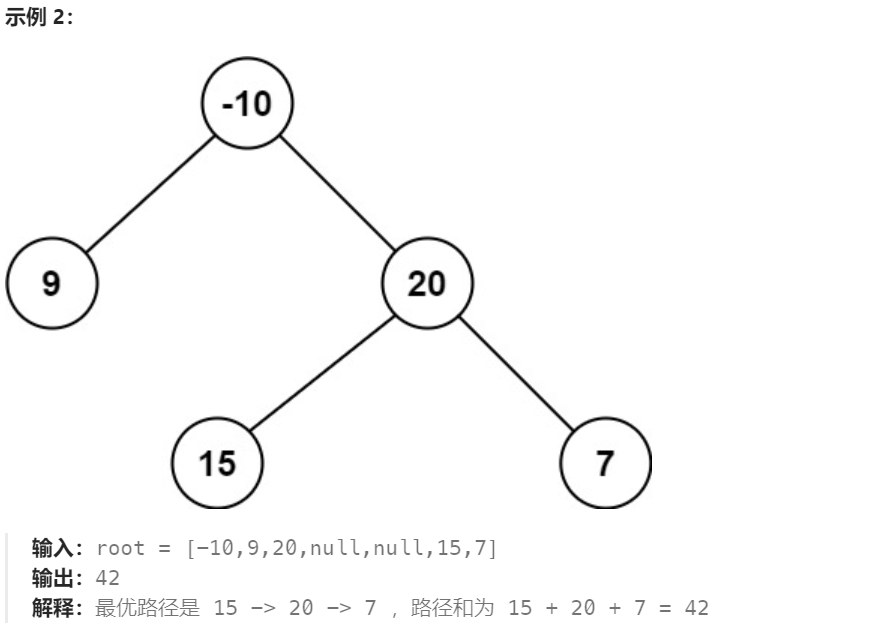
leetcode:https://leetcode.cn/problems/binary-tree-maximum-path-sum/description/
难度:【困难】
二. 思路分析
1. 核心点
对于任意一个节点来说(不算父节点的情况下),可以获取到的最大路径和一定是:
nodeMax=node.value + 左子树能提供的最大值 + 右子树能提供的最大值 (没有左右子树, 按照0计算)
2. 是不是缺失考虑父节点的情况呢?
没有, 因为在去考虑父节点的左右子树的时候,自然就将左右子节点的父节点考虑进去了

三. 代码实操
class TreeNode {
val: number;
left: TreeNode | null;
right: TreeNode | null;
constructor(val: number, left?: TreeNode | null, right?: TreeNode | null) {
this.val = val === undefined ? 0 : val;
this.left = left === undefined ? null : left;
this.right = right === undefined ? null : right;
}
}
/**
* 求最大路径和
* @param root 根节点
* @returns 最大路径的和
*/
function maxPathSum(root: TreeNode | null): number {
let maxSum = -Infinity; //负无穷大
//定义内部函数,进行递归操作
function dfs(node: TreeNode | null): number {
if (!node) return 0;
//左右子树计算可以提供的非0最大值
const leftSum = Math.max(dfs(node.left), 0);
const rightSum = Math.max(dfs(node.right), 0);
//当前节点能获得到的最大值
const pathSum = node.val + leftSum + rightSum;
maxSum = Math.max(pathSum, maxSum);
//返回当前节点中能获取的最大值
return node.val + Math.max(leftSum, rightSum);
}
//调用递归
dfs(root);
return maxSum;
}
三.
!
- 作 者 : Yaopengfei(姚鹏飞)
- 博客地址 : http://www.cnblogs.com/yaopengfei/
- 声 明1 : 如有错误,欢迎讨论,请勿谩骂^_^。
- 声 明2 : 原创博客请在转载时保留原文链接或在文章开头加上本人博客地址,否则保留追究法律责任的权利。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号