第十八节:动态规划面试题(爬楼梯、买卖股票时机、最大子数组和)
一. 爬楼梯
1. 题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
详见: https://leetcode.cn/problems/climbing-stairs/description/
2. 分析
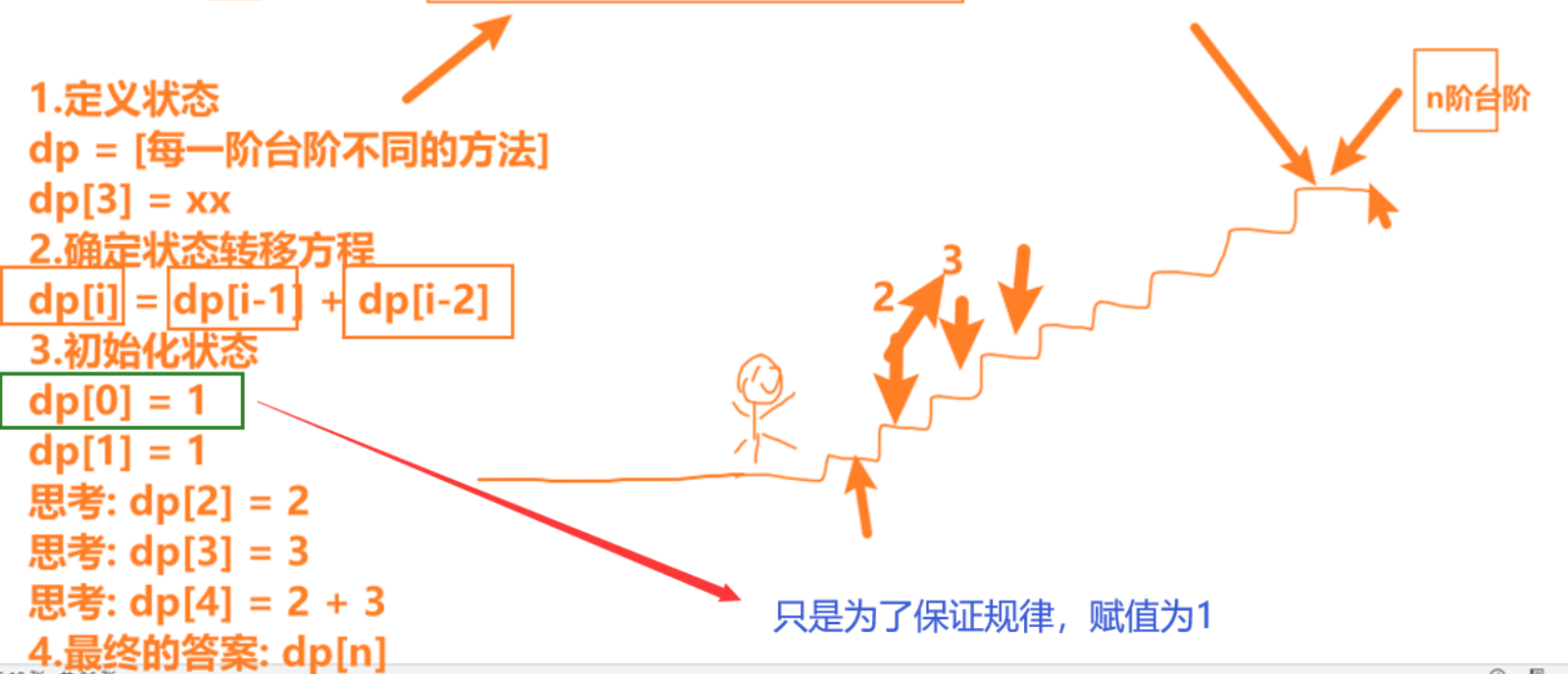
(1).根据题目可知, 每次只能跳1个或2个台阶, 所有要跳到n阶, 要么从(n-1)阶跳1个台阶上去; 要么从(n-2)阶跳2个台阶上去,从而推导出来状态转移方程。
(2). 定义状态
dp[n] 表示爬到第n阶台阶的方法数
dp[n-1] 表示爬到第n-1阶台阶的方法数
dp[n-2] 表示爬到第n-2阶台阶的方法数
即dp[]数组表示爬到第i阶台阶的方法数
(3). 初始化状态
根据画图可知,详见画图
dp[1]=1;
dp[2]=2;
dp[3]=3; [A.一次1阶,跳3次 B.先1阶,后2阶 C.先2阶,后1阶]
dp[4]=5; [不再列举了]
可以推导出来规律:dp[3]=dp[2]+dp[1]; dp[4]=dp[3]+dp[2]; dp[2]=dp[1]+dp[0]; 虽然dp[0]没有意义, 这里为了方便计算,保持上述规律,将dp[0]赋值为1
(4). 确定状态转移方程
根据上述(3)可以推导出来,根据题意也可以直接想到 dp[n]=dp[n-1]+dp[n-2]
(5). dp[n] 即为最终答案
/**
* 爬楼梯
* @param n 第n阶的方法数
*/
function climbStairs(n: number): number {
if (n <= 0) return 0; //防止越界
//1. 定义状态
let dp: number[] = [];
//2.初始化状态
dp[0] = 1;
dp[1] = 1;
//3.确定状态转移方程
for (let i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
//4. 返回最终结果
return dp[n];
}3. 状态压缩
function climbStairs(n: number): number {
//边界判断
if (n === 1) return 1;
if (n <= 0) return 0;
//1. 定义状态并初始化状态
let pre = 1; //dp[0]
let current = 1; //dp[1]
//2.确定状态转移方程
for (let i = 2; i <= n; i++) {
let res = current + pre;
pre = current;
current = res;
}
//3. 返回最终结果
return current;
}
二. 买卖股票时机
1. 题目说明
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/description/
示例:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意:利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
2. 思路分析
(1).定义状态
dp[i] 表示第i天卖出所能获得最大利润 , dp[0]表示第0天, 没有实际意义。
(2).初始化状态
dp[0]=0 没有实际意义
dp[1]=0 第一天没法既买又卖, 所以赋值为0
dp[2]=1-7=-6
dp[3]=5-1=4
dp[4]=3-1=2
(3).确定状态转移方程
dp[i]=price[i-1]-preMinPrice , 其中preMinPrice表示的是price[0,i-1)中的最小值
这里需要注意:prices数组中的 price[0] 在题目中表示的是第1天的价格
(4). 求最大利润
对dp数组求最大值
/**
* 动态规划1
* @param prices 彩票价格数组
* @returns 最大利润
*/
function maxProfit(prices: number[]): number {
//1. 定义状态
let dp: number[] = [];
//2. 初始化状态
dp[0] = 0; //第0天 没有意义
dp[1] = 0; //第1天
//3.确定状态转移方程
let preMinPrice = prices[0];
for (let i = 2; i <= prices.length; i++) {
dp[i] = prices[i - 1] - preMinPrice;
preMinPrice = Math.min(prices[i - 1], preMinPrice);
}
//4. 求最大利润-对数组求最大值
return Math.max(...dp);
}
3. 继续优化
上述方案最后一步需要对dp数组求最大值, 浪费了一部分性能,在这里对其进行优化。
(1). 定义状态
设 dp[i] 表示前 i 天中能够获取的最大利润!!!
(2).初始化状态
dp[0]=0 没有实际意义
dp[1]=0 第一天没法既买又卖, 所以赋值为0
dp[2]=1-7=-6
dp[3]=5-1=4
dp[4] 比较(3-1) 和 dp[3]的大小,由于 2<4, 所以dp[4]=4
(3).确定状态转移方程
dp[i]= Math.Max(price[i-1]-preMinPrice,dp[i-1] ), 其中preMinPrice表示的是price[0,i-1)中的最小值
解释:dp[i] 需要比较 第i天卖出的最大值 和 dp[i-1] 大小,求最大值
这里需要注意:prices数组中的 price[0] 在题目中表示的是第1天的价格
(4).求最大利润
即 dp[prices.length] 即可
/**
* 动态规划2
* @param prices 彩票价格数组
* @returns 最大利润
*/
function maxProfit2(prices: number[]): number {
//1. 定义状态
let dp: number[] = [];
//2. 初始化状态
dp[0] = 0; //第0天 没有意义
dp[1] = 0; //第1天
//3.确定状态转移方程
let preMinPrice = prices[0];
for (let i = 2; i <= prices.length; i++) {
dp[i] = Math.max(prices[i - 1] - preMinPrice, dp[i - 1]);
preMinPrice = Math.min(prices[i - 1], preMinPrice);
}
//4. 求最大利润
return dp[prices.length];
}4. 状态压缩
/**
* 动态规划-状态压缩
* @param prices 彩票价格数组
* @returns 最大利润
*/
function maxProfit(prices: number[]): number {
//1. 定义状态 并且 初始化状态
let preMaxProfit = 0; //前一个状态的最大利润
//3.确定状态转移方程
let preMinPrice = prices[0];
for (let i = 2; i <= prices.length; i++) {
preMaxProfit = Math.max(prices[i - 1] - preMinPrice, preMaxProfit);
preMinPrice = Math.min(prices[i - 1], preMinPrice);
}
//4. 求最大利润
return preMaxProfit;
}
三. 最大子数组和
1. 题目说明
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6
https://leetcode.cn/problems/maximum-subarray/description/
2. 思路分析
(1). 定义状态
dp[i] 表示第i位置最大连续子数组的和
(2). 初始化状态
dp[0]=nums[0]=-2;
dp[1]= 1; 比较 nums[1] 和 nums[1]+dp[0]的大小,求最大值
dp[2]=-2; 比较 nums[2] 和 nums[2]+dp[1]的大小,求最大值
(3). 确定状态转移方程
dp[i]=Math.Max(nums[i], nums[i]+dp(n-1) )
解释:
如果前面的子序列是负数,那么最大子序列和一定是自己;
如果前面的子序列是正数,那么最大子序列和是自己+前值;
(4). 求最大值
即求dp数组的最大值
/**
* 求 最大子数组的和
* @param nums 输入数组
* @returns 连续子数组和的最大值
*/
function maxSubArray(nums: number[]): number {
// 1. 定义状态
let dp: number[] = [];
//2. 初始化状态
dp[0] = nums[0];
//3. 确定状态转移方程
for (let i = 1; i < nums.length; i++) {
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
}
//4. 求最大值
return Math.max(...dp);
}3. 继续优化
上述方案最后一步需要对dp数组求最大值, 浪费了一部分性能,在这里对其进行优化。
设 dp[i] 表示前 i 位置中能够获取的最大和
优化方式同买卖股票
4. 继续优化
在动态规划算法中,我们需要定义一个一维数组 dp,其中dp[i] 表示以第 i 个元素结尾的子数组的最大和。 根据动态转移方程 dp[i] = max(dp[i-1] + nums[i], nums[i]),我们可以计算出 dp 数组中的每个元素,从而求解原问题。
这个算法的空间复杂度为 O(n)。
然而,我们可以发现,dp 数组中的每个元素只与前一个元素有关。
因此,我们可以使用滚动数组的技巧,将一维数组 dp 压缩成一个变量preMaxSum,从而将空间复杂度优化为 O(1)。
/**
* 求 最大子数组的和
* @param nums 输入数组
* @returns 连续子数组和的最大值
*/
function maxSubArray(nums: number[]): number {
// 1. 定义状态 和 初始化状态
let preMaxSum = nums[0];
//3. 确定状态转移方程
let maxSum = preMaxSum;
for (let i = 1; i < nums.length; i++) {
preMaxSum = Math.max(nums[i], nums[i] + preMaxSum);
maxSum = Math.max(maxSum, preMaxSum);
}
//4. 求最大值
return maxSum;
}
!
- 作 者 : Yaopengfei(姚鹏飞)
- 博客地址 : http://www.cnblogs.com/yaopengfei/
- 声 明1 : 如有错误,欢迎讨论,请勿谩骂^_^。
- 声 明2 : 原创博客请在转载时保留原文链接或在文章开头加上本人博客地址,否则保留追究法律责任的权利。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号