boosting 提升方法实际采用的是加法模型和前向分步算法 【之前在讲 Adaboost 时,讲过这两个算法,参考我的博客】
提升树 boosting tree
以决策树为基学习器的提升方法称为提升树,提升树可以解决分类和回归问题,分类问题以分类树为基学习器,回归问题以回归树为基学习器,决策树均为二叉树。
提升树模型可以表示为
![]()
M为决策树个数,T(x, θ) 为决策树模型, θ为决策树参数
提升树算法采用前向分步算法,初始提升树 f0(x)=0,第m步提升树
![]()
fm-1(x) 是当前模型,相当于是个已知数,模型误差可以表示为
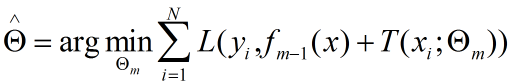
由于 fm-1(x) 是个常数,y也是常数,最小化误差就是求 T(x, θ) 中的 最优θ,也就是只求第 m 步的最佳模型,所以是一种贪心算法。
不同类型的提升树有不同的损失函数,回归问题就是均方误差,分类问题为指数损失函数
![]()
当yy相同时,损失函数趋近于0
回归提升树
由于分类树比较常见,所以这里主要讲回归问题。
回归树
假设数据样本为
![]() ,x为输入空间,输入空间为实数域, 【回归问题中 x 一般为连续值,处理方式类似于决策树处理连续值】
,x为输入空间,输入空间为实数域, 【回归问题中 x 一般为连续值,处理方式类似于决策树处理连续值】
将 x 划分成 J 个互不相交的区域,R1、R2、R3...RJ,每个区域的输出为 cj,决策树可表示为
![]()
具体理解如图
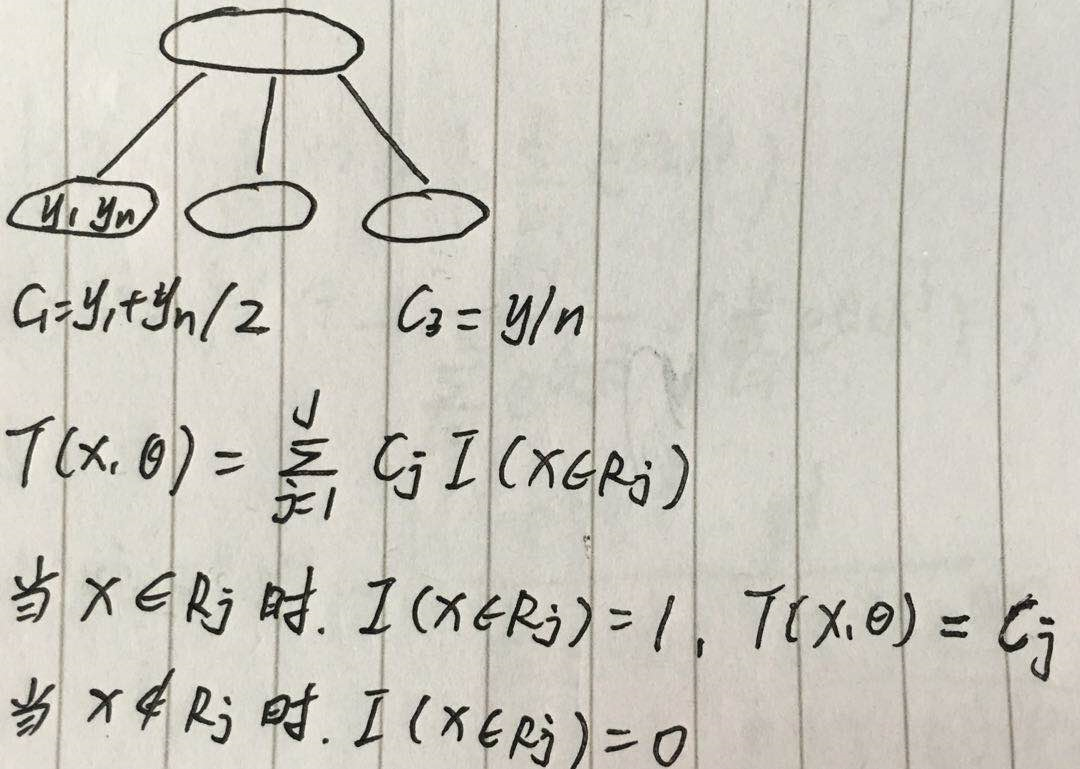
可以看到 J 就是叶节点的个数,也表示了决策树的复杂度,只分裂一次的树称为 树桩
回归提升树
依然采用前向分步算法
1. 初始提升树 f0(x)=0
2. 第 m 步训练决策树 T(x, θ),得到该步的提升树
![]()
需要最优化 θ
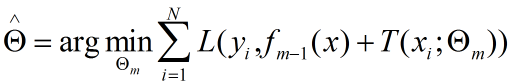
回归问题损失函数为 均方差
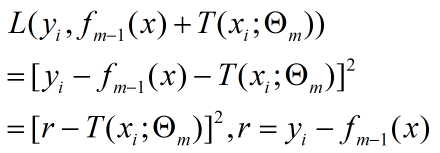
r 就是当前模型的残差,所以 提升树 只需学习当前模型的残差,这使得算法变得简单。
3. 输出组合模型
回归提升树算法总结
输入:![]()
输出:![]()
1)初始提升树 f0(x)=0
2)对 m = 1,2,3...M
3)计算残差 r= yi - fm-1(x)
4)拟合fm-1的残差 r 学习一个回归树 T(x, θ) 【注意,每步要更新 f(x),f(x)是前n步的和,而不是计算单步的残差,损失】
5)更新![]()
6)输出回归提升树![]()
实例
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 5.56 | 5.70 | 5.91 | 6.40 | 6.80 | 7.05 | 8.90 | 8.70 | 9.00 | 9.05 |
以树桩作为基学习器。
1. 求 T1(x) ====> 将样本集按x分成2分,分别求平均即可,那如何分呢?
目标函数为
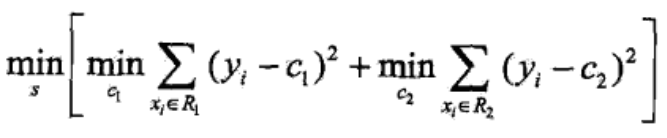
当 x 属于 R1时,y_predict = c1,误差 y-c1,同理,最终得到上面的损失函数,当损失函数最小时,其对应的划分方式就是最佳划分方式。
下面就是按决策树处理连续值的方式
划分点s为 [1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5]
R1 = {x|x<s};R2={x|x>s}
对叶子结点求平均即可求得 c1,c2
经计算,当 s = 1.5 时,c1 = 5.56,c2 = 7.50,

同理可得到所有划分的损失
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 | |
| m(s) | 15.72 | 12.07 | 8.36 | 5.78 | 3.91 | 1.93 | 8.01 | 11.73 | 15.74 |
可见,当 s = 6.5 时,损失最小,为1.93,此时 c1 = 6.24,c2 = 8.91,回归树为
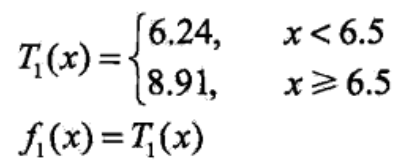
当前残差
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | -0.68 | -0.54 | -0.33 | 0.16 | 0.56 | 0.81 | -0.01 | -0.21 | 0.09 |
0.14 |
当前损失
![]()
第一步只是个弱学习器,可见效果不怎么地
2. 求 T2(x) ====> 此时只需学习 T1(x) 的残差
方法同第一步,回归树为
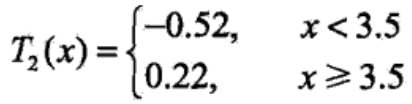
当前损失
注意损失是 f2(x) 的损失,残差也是 f2(x) 的残差,而不是 T2(x) 的损失,所以先计算 f2(x)

损失为 0.79,比1.93要小。
3. 继续求 Tm(x) ====> 此时只需学习 fm-1(x) 的残差
比如学习 6 个回归树,则最终模型为

损失为 0.17,比之前要小很多。
现在我们需要考虑几个问题
1. 上述基学习器 只是 一层,如果是2层、3层,那么基学习器如何表示?会相当麻烦
2. 多层的基学习器又如何相加呢?更麻烦
3. 提升树的基学习器通过最小化均方差来学习,如果损失函数不是 均方差,又如何?
为了解决上述问题,有人提出了改进算法。
梯度提升树 GBDT
GBDT 也可以解决回归和分类问题,有些地方把 回归 GBDT 叫做 GBRT。
GBDT 损失函数可以有多种,在 sklearn 中,回归问题损失函数有4种:ls 平方损失,lad 绝对损失,huber huber损失,quantile:分位数损失,分类问题损失函数有2种:exponential 指数损失,deviance 对数损失
GBDT 利用梯度下降的近似方法,其 关键是利用 损失函数的负梯度 在当前模型的值 作为 回归提升树中残差的近似。

第 m 轮第 i 个样本的损失函数的负梯度,得到 (xi,rmi) 作为新数据,拟合一个回归树
具体算法如下
输入:![]() ,损失函数 L(y,f(x))
,损失函数 L(y,f(x))
输出:回归树组合模型F(x)
1)初始化提升树 ====> 估计一个使得损失函数最小的常数c,他只有根节点,如果loss是mes,一般取均值,如果loss是绝对损失,一般取中位数
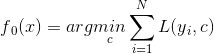
2)for m = 1,2...M ====> 训练M个基学习器
3)for i = 1,2...N ====> 遍历N个样本,计算残差 【为什么带负号,因为f(x)是自变量,在损失函数中它前面有个减号,求导时相当于复合函数,得乘以-1,前面带个负号,刚好和这个-1抵消,r=y-f(x)】

4)拟合一棵cart树,对x进行划分,建立决策树,得到第m棵树的叶节点区域 Rmj,j=1,2..J (j表示叶节点的个数)
5)for j=1,2...J ====> 遍历 J 个叶节点,利用线性搜索,估计每个叶节点的值,使得损失函数最小化
c=βf(x),决策树只是输出了 f(x),但是 β 是多少,需要根据 min loss 求解,最终把 c 作为叶子结点的输出
![]()
6)更新模型

7)输出回归树
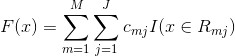
实例
数据如下:5个样本,4个训练,1个测试,特征为年龄、体重,标签为身高
| 编号 | 年龄(岁) | 体重(kg) | 身高(m)(标签值) |
|---|---|---|---|
| 0 | 5 | 20 | 1.1 |
| 1 | 7 | 30 | 1.3 |
| 2 | 21 | 70 | 1.7 |
| 3 | 30 | 60 | 1.8 |
| 4 | 25 | 65 | 预测 |
参数设置
迭代次数:n_trees = 5
树的深度:max_depth = 3
学习率:lr = 0.1
损失函数:mes
1. 初始化提升树 ,loss为mes,取均值即可 f0(x) = 1.475
也可以正规求,估计一个使得损失函数最小的常数,loss = Σ(y_true - y_pred)2,要最小,求导,Σ(y_true - y_pred)=Σy_true - Σy_pred=Σy_true - Ny_pred
令导数等于0,y_pred = Σy_true / N,即均值
2. 计算 f0(x) 的近似残差
| 编号 | 真实值 | f0(x) | 残差 |
| 0 | 1.1 | 1.475 | -0.375 |
| 1 | 1.3 | 1.475 | -0.175 |
| 2 | 1.7 | 1.475 | 0.225 |
| 3 | 1.8 | 1.475 | 0.325 |
此时残差变成了真实的标签
3. 基于特征的划分
| 划分点 | 小于划分点的样本 | 大于等于划分点的样本 | SSElSSSEl | SErSEr | SEsumSEsum |
|---|---|---|---|---|---|
| 年龄5 | / | 0,1,2,3 | 0 | 0.327 | 0.327 |
| 年龄7 | 0 | 1,2,3 | 0 | 0.140 | 0.140 |
| 年龄21 | 0,1 | 2,3 | 0.020 | 0.005 | 0.025 |
| 年龄30 | 0,1,2 | 3 | 0.187 | 0 | 0.187 |
| 体重20 | / | 0,1,2,3 | 0 | 0.327 | 0.327 |
| 体重30 | 0 | 1,2,3 | 0 | 0.140 | 0.140 |
| 体重60 | 0,1 | 2,3 | 0.020 | 0.005 | 0.025 |
| 体重70 | 0,1,3 | 2 | 0.260 | 0 | 0.260 |
损失函数是mes,我们这里简单计算每个叶节点的平方和损失,上图第4列是左节点的损失,第5列是右节点的损失,以年龄7为例,右节点损失计算如下

误差最小为0.025,有两种划分方式,随便选一种,年龄21,做如下划分
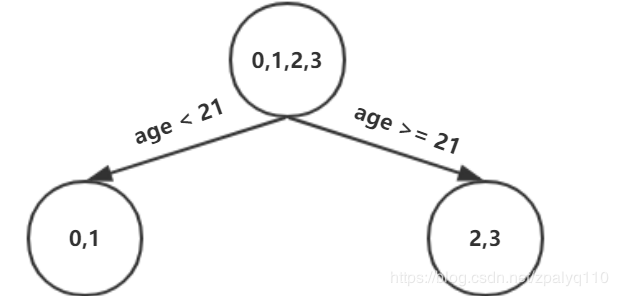
max_depth 为3,还需继续划分,同理可得
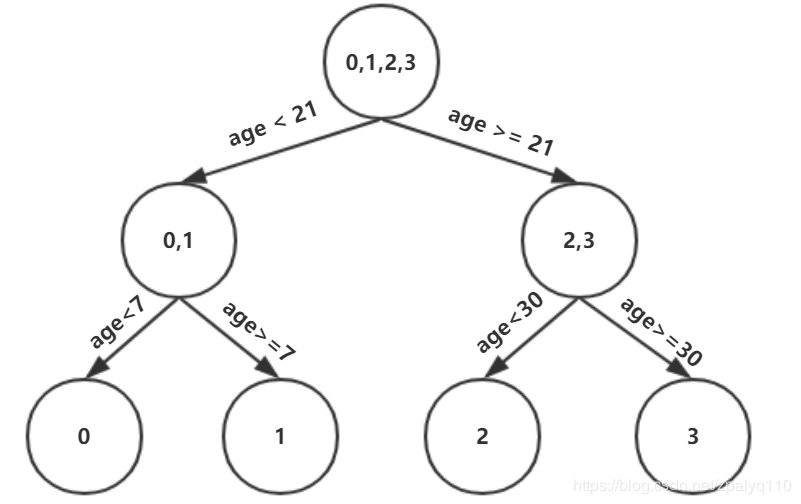
4)计算叶节点的值 【关键点】
遍历叶节点,线性搜索,计算节点值,使得损失函数最小
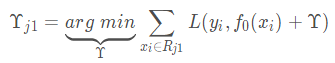
r 其实就是基学习器,f0(x) 是之前基学习的和,f0(x)+r 就是本次预测,yi为真实值,最初的真实值
相当于给节点找一个参数r,使得损失函数最小,方法是求导,令导数等于0,计算可得
r11 = -0.375,r12 = -0.175,r21 = 0.225,r22 = 0.325
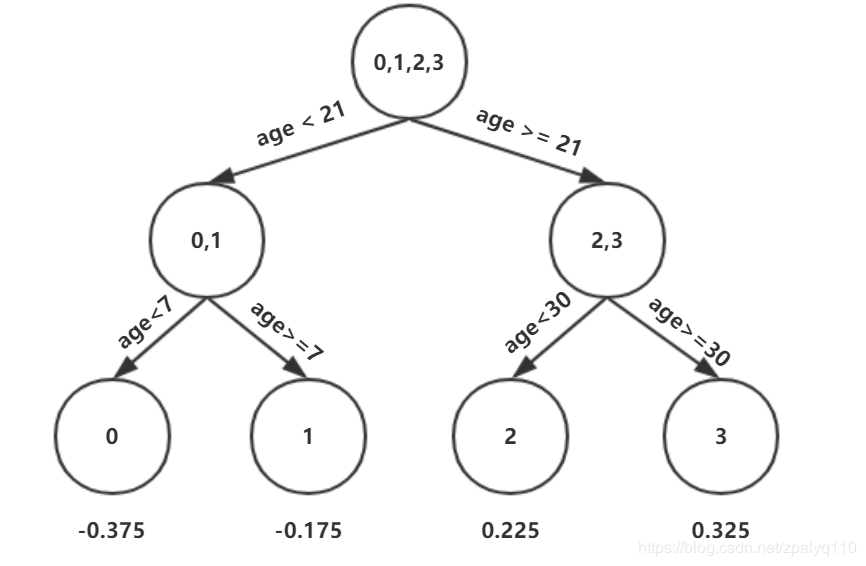
5)更新模型

6)重复上述步骤即可
注意
1. 提升树的基学习器只能是 cart 树
2. 加法模型可以带学习率,放慢学习速度,防止过拟合
参考资料:
《统计学习方法》 李航



 浙公网安备 33010602011771号
浙公网安备 33010602011771号