序列

https://www.zybuluo.com/ysner/note/1225147

题面

我们可以对任一序列\(S\)构造笛卡尔树。笛卡尔树是一棵二叉树,它符合小根堆的性质,并且它的中序遍历就是该序列。如果序列中的数两两不同,那么笛卡尔树是唯一的。以下是一个笛卡尔树的例子:

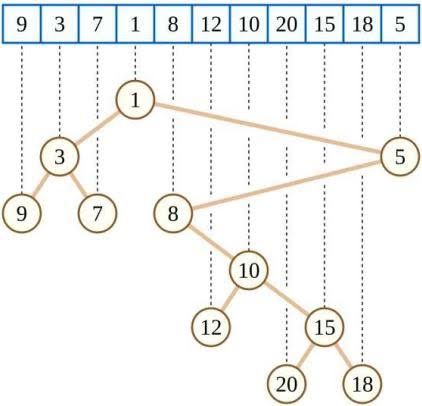
（概括一下，就是每次在当前区间中选出值最小结点作为根，然后把根两边区间分别的最小值作为根的两个儿子，然后再分别取根两边区间向下递归）
如此定义一棵笛卡尔树的\(AK\)值:

• 如果一个节点有两个儿子\(a,b\),则该节点的\(AK\)值为\(|w_u-w_v|\)。
• 如果一个节点有少于两个儿子,则该节点的\(AK\)值为\(0\)。
• 一棵树的\(AK\)值为其所有节点的\(AK\)权值之和。

询问如果以所有\(n\)的排列构建笛卡尔树，那么其中\(AK\)值不超过\(m\)的个数。

• \(30pts\) \(n\leq10\)
• \(50pts\) \(m=0,1,2,3\)
• \(100pts\) \(n,m\leq150\)

吐嘈

认真表示此题和分组一题极为相似，我考场上竟然没切掉。。。
或许是因为我没有认真考虑加排列的过程，而是认为排列是既成的。

解析

\(30pts\)算法

我是不会承认我看了一小时图才发现正确建树方式的
暴枚排列+模拟建树，复杂度\(O(2^nlogn)\)。

\(20pts\)算法

\(m\)只有\(4\)种取值，还这么小？
这是不是叫我们打表找规律。。。
\(m=0\)时，\(f[i][0]=2^{n-1}\)😭\(i\geq3)\)
\(m=1\)时，\(f[i][3]=f[i-1][4]*4+2^{i-2}\)(\(i\geq3,f[3][5]=2\))
\(m=2\)时，\(f[i][2]=f[i-1][2]*6+2^{i-2}\)(\(i\geq4,f[4][2]=4\))
\(m=3\)时，并不知道是什么规律。
于是回答\(\sum^m_{i=0}f[n][i]\)就可以了。

\(100pts\)算法

显然，建树是有一个过程的。
我们每给当前的排列从小到大加一个数，就有几种决策：

• 新结点接在一个叶子（未匹配）结点上
• 新结点与另一结点配对，产生\(AK\)值

依照决策，我们似乎能猜猜状态：\(f[i][j][k]\)表示当前排列有\(i\)个数，\(AK\)值为\(j\)，有\(k\)个结点可匹配的方案数。
但是，这么\(DP\)就有一个问题，你并不知道新结点是与哪个结点匹配的，因而无法求得\(AK\)值。
我们可以用一种很套路的差分方法，就是新点接在叶子结点上时减去新点权值，等它被匹配时再加上匹配点的权值。
但是并不一定所有点都会被匹配啊！
所以，我们还要多一维状态\(f[i][j][k][l]\)，\(l\)维表示当前有\(k\)个结点最后被匹配完毕的方案数（而\(总共l\)个结点并不一定被匹配）。
第一个决策也要分为两类：新结点将匹配和新结点将不匹配。于是\(3\)个决策。

第二个问题是\(j\)按差分方法很有可能减着减着就成负数了。
想一想，每当我们加一个数，就相当于让所有的还未配对完毕的\(|w_u-w_v|\)都加\(1\)。
因为它们要更晚才能被配对。
因此，每次转移时，\(j+=l\)即可。

好像新结点接在未匹配结点上的方案数也值得思考。
注意到，\(1\)个结点能接\(2\)个，而每加一个结点，占用了\(1\)个能接的位置，又能接\(2\)个。因此，每加一个结点，能接的位置+\(1\)。
即\(i\)个结点能接\(i+1\)个。
而又有\(k\)个位置是不能占的，因此方案数为\(i+1-k\)。

时间复杂度上限\(O(n^4)\),空间复杂度滚动后\(O(n^3)\)。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define re register
#define il inline
#define ll long long
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define fp(i,a,b) for(re int i=a;i<=b;i++)
#define fq(i,a,b) for(re int i=a;i>=b;i--)
using namespace std;
int n,m,mod,f[2][155][155][155],now,nxt=1;
ll ans;
bool vis[200];
il ll gi()
{
  re ll x=0,t=1;
  re char ch=getchar();
  while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
  if(ch=='-') t=-1,ch=getchar();
  while(ch>='0'&&ch<='9') x=x*10+ch-48,ch=getchar();
  return x*t;
}
int main()
{
  freopen("seq.in","r",stdin);
  freopen("seq.out","w",stdout);
  n=gi();m=gi();mod=gi();
  f[1][0][0][0]=1;
  fp(i,1,n-1)
  {
    fp(j,0,m)
      fp(k,0,i)
        fp(l,k,i)
        {
          re int tmp=f[nxt][j][k][l],t=j+k;f[nxt][j][k][l]=0;
	  if(!tmp||t>m) continue;
	  if(k) (f[now][t][k-1][l-1]+=1ll*tmp*k%mod)%=mod;
	  if(i+1-l>0) (f[now][t][k][l+1]+=1ll*tmp*(i+1-l)%mod)%=mod;
	  if(i+1-l>0) (f[now][t][k+1][l+1]+=1ll*tmp*(i+1-l)%mod)%=mod;
	}
    swap(now,nxt);
  }
  fp(j,0,m)
    fp(l,0,n)
    (ans+=f[nxt][j][0][l])%=mod;
  printf("%lld\n",ans);
  fclose(stdin);
  fclose(stdout);
  return 0;
}