经典算法-贪心

参考：

算法(六):图解贪婪算法

贪心算法秘籍

概念：

一个贪心算法总是做出当前最好的选择，也就是说，它期望通过局部最优选择从而得到全局最优的解决方案

（1）贪心选择

所谓贪心选择性质是指原问题的整体最优解可以通过一系列局部最优的选择得到。

应用同一规则，将原问题变为一个相似的但规模更小的子问题，而后的每一步都是当前最佳的选择。

这种选择依赖于已做出的选择，但不依赖于未做出的选择。运用贪心策略解决的问题在程序的运行过程中无回溯过程。

关于贪心选择性质，读者可在后续的贪心策略状态空间图中得到深刻的体会。

（2）最优子结构

当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。

问题的最优子结构性质是该问题是否可用贪心算法求解的关键。

例如原问题S={a1，a2，…，ai，…，an}，通过贪心选择选出一个当前最优解{ai}之后，转化为求解子问题S−{ai}，

如果原问题的最优解包含子问题的最优解，则说明该问题满足最优子结构性质，如图2-1所示。

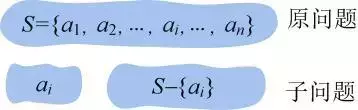
题目：gas-station

题目描述
环形路上有n个加油站，第i个加油站的汽油量是gas[i].
你有一辆车，车的油箱可以无限装汽油。从加油站i走到下一个加油站（i+1）花费的油量是cost[i]，你从一个加油站出发，刚开始的时候油箱里面没有汽油。
求从哪个加油站出发可以在环形路上走一圈。返回加油站的下标，如果没有答案的话返回-1。
注意：
答案保证唯一。

public class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int start=gas.length-1;
        int end=0;
        int sum=gas[start]-cost[start];
        while(end<start){
            if(sum<0){
                start--;
                sum+=gas[start]-cost[start];
            }else{
                sum+=gas[end]-cost[end];
                end++; 
            }
        }
        if(sum>=0){
            return start;
        }else{
            return -1;
        }
    }
}

参考：

https://blog.csdn.net/ibelieve8013/article/details/103247662

https://blog.csdn.net/u010244645/article/details/69326752

解题思路：

如果我随便选个起点，然后选择它的下一个加油站为终点，然后计算剩余油量，如果始终是大于零，终点就往后移，

直到最后终点又跑到了起点的位置，说明我们的起点是合适的，就是最终的下标。但是世事不尽如人意，哪里那么合适，

一旦我们发现剩余油量小于零之后，那么说明这个起点是不行的了，我们应该把起点回退，重新再试，

注意，这个时候，已经计算过的路程是没有必要再计算了，所以终点仍然是在那里，起点回退，一旦到了剩余油量又有了，

那么终点继续往后移。直到所有的点遍历完全，这个就是整体的思路了。

但是我们想想，如果起点在下标为0的位置，它回退，往哪里退呢，这是个数组，退到最后一个，最后一个又往前退，这个实现起来就比较繁琐了，

最妙的思路就来了：我们如果一开始就把start设置在最后一个下标，而把end设置在它的下一个，也就是第0个下标处，

那么这个繁琐的事情是不是就省去了