基于时频域霍夫变换的汽车雷达互干扰抑制——论文阅读 - 指南

基于时频域霍夫变换的汽车雷达互干扰抑制

Y. Li, W. Zhang and L. Ji, “Automotive Radar Mutual Interference Mitigation Based on Power-Weighted Hough Transform in the Time-Frequency Domain,” in IEEE Transactions on Vehicular Technology, vol. 74, no. 3, pp. 3854-3869, March 2025, doi: 10.1109/TVT.2024.3489628.

随着高级驾驶辅助框架（ADAS）和自动驾驶技巧的发展，毫米波雷达因其全天候、全天时的工作能力而成为不可或情的传感器。然而，道路上配备雷达的车辆密度迅速增加，导致雷达信号之间的相互干扰挑战日益严重。这种干扰表现为瞬时、高功率的噪声，会严重降低雷达的目标检测性能，增加目标丢失的概率，对驾驶安全构成直接威胁。

：就是本文提出了一种创新的干扰抑制方法，其核心思想目标回波和干扰信号在经过FMCW雷达混频处理（解啁啾）后，在时频（TF）域中具有截然不同的结构特征。该方法利用霍夫变换（一种经典的直线检测技术）来精准识别并定位干扰在时频图上的线性结构，然后通过自回归（AR）模型恢复被干扰区域的有用信号。

---

核心数学模型：信号、回波与干扰

文章首先建立了线性调频连续波（FMCW）雷达的信号模型，这是理解干扰特性的基础。

1. FMCW发射信号 ($s_t(t)$)

FMCW雷达发射的是一种“啁啾”信号，即频率随时间线性变化的信号。其数学表达式为：
$$s_t(t)=\sqrt{2P_t}\cos [2\pi (f_c+\frac{1}{2}kt)t]$$
其中，$P_t$是发射功率，$f_c$是中心载频，$k$是调频斜率，由带宽$B$ 和扫描时间 $T$ 决定，即 $k=B/T$。

2. 目标回波信号 ($s_e(t)$)

发射信号的延迟版本。电磁波经历了“雷达 -> 目标 -> 雷达”的双程传播，因此其功率就是目标回波$P_e$ 与距离 $R$ 的四次方（$1/R^4$）成反比。

3. 干扰信号 ($s_i(t)$)

干扰信号来自另一部（干扰）雷达，它通常具有不同的中心频率$f_{ci}$ 和调频斜率 $k_i$。其数学表达式为：
$$s_i(t)=\sqrt{2P_i}\cos [2\pi f_{ci}(t-{\tau }_i)+\frac{1}{2}{k}_i(t-{\tau }_i{)}^2]$$
至关重要的是，干扰信号只经历了“干扰雷达 -> 本车雷达”的单程传播，因此其功率$P_i$ 仅与距离 $R_i$ 的平方（$1/R_i^2$）成反比。

4. 信号干扰比 (SIR)

由于传播路径的差异（$1/R^4$ vs $1/R_i^2$），干扰信号的功率衰减远慢于目标回波。这导致了极低的信号干扰比（SIR）：
$$SIR=\frac{P_e}{P_i}=\frac{R_i^2\sigma }{4\pi R^4}$$
如论文中的表I所示，一个100米处的干扰源（如另一辆车）产生的干扰功率可能比100米处目标回波的功率强41dB2000米外的干扰源，其干扰功率也可能强就是，即使15dB。这意味着干扰信号的幅度远大于有用信号。

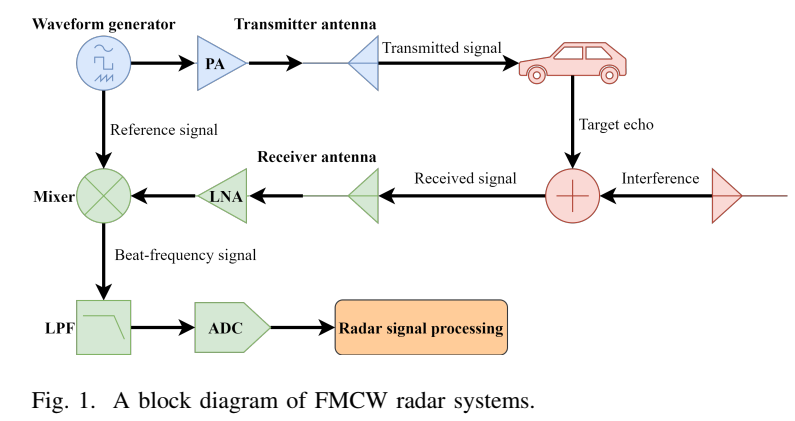
图1展示了FMCW雷达体系的框图，接收信号$s_r(t)$ 是目标回波 $s_e(t)$、干扰 $s_i(t)$ 和噪声 $g(t)$ 的总和。

5. 差频信号 (Beat-Frequency Signal)

FMCW雷达的核心处理步骤是“解啁啾”（Dechirp），即将接收信号与本地参考信号（即发射信号$s_t(t)$）进行混频，然后通过一个低通滤波器（LPF）。这一步骤产生了关键的差频信号，也揭示了目标与干扰的根本区别：

• 目标差频 ($f_b$)：目标回波 $s_e(t)$ 与参考信号 $s_t(t)$混频后，由于二者具有相同的调频斜率$k$，它们相减后$t^2$项被消除，产生一个恒定频率的信号。这个频率（$f_b$）与目标距离成正比：
  $$f_b=k\tau$$

• 干扰差频 ($f_{bi}$)：干扰信号 $s_i(t)$ 与参考信号 $s_t(t)$混频后，由于二者的调频斜率不同（$k\ne k_i$），$t^2$项无法消除。其差频信号一个LFM信号就是仍然（即线性调频信号），其瞬时频率$f_{bi}$ 是时间 $t$的线性函数：
  $$f_{bi}=f_c-f_{ci}+k_i{\tau }_i+\frac{1}{2}(k-k_i)t$$

图2极好地在视觉上总结了这一核心差异。

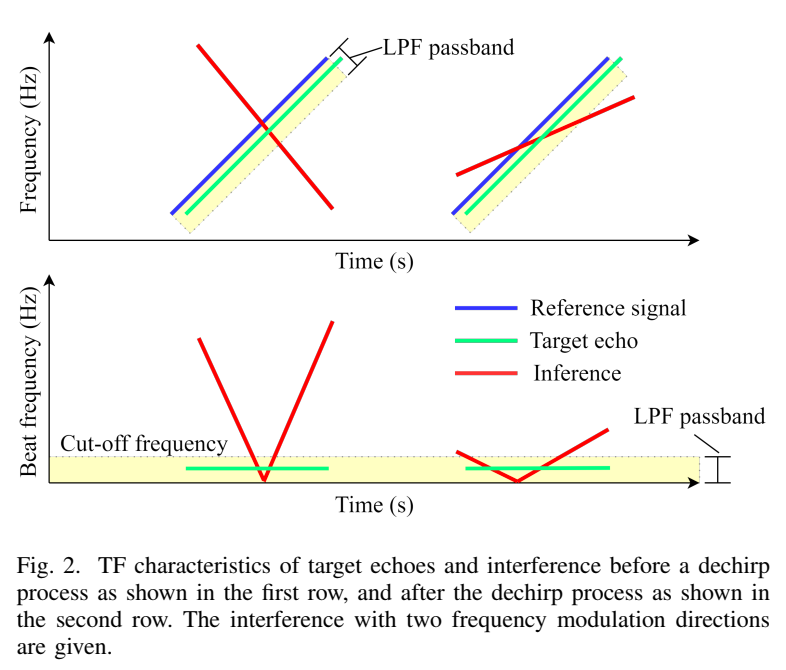
• 上排 (解啁啾前)：目标回波和干扰都是倾斜的LFM信号。
• 下排 (解啁啾后)：经过混频和LPF（黄色区域），目标回波（绿色） 变成了一条水平直线（恒定频率）；而干扰信号（红色） 仍然是一条倾斜的直线（LFM信号），并且由于LPF的滤波，它在时间上是有限的。

---

论文的核心方法：功率加权霍夫变换与AR恢复

利用上述“目标是水平线，干扰是倾斜线”的关键物理特性，本文设计了一套精巧的干扰抑制流程。

1. 动机分析

现有的干扰检测方法（如基于恒定虚警率CFAR的方法）依赖于干扰的幅度远大于噪声，但在低信噪比（SNR）或弱干扰下性能会急剧下降。

本文的动机是，不应仅仅依赖幅度信息，更应利用干扰在时频域中清晰的结构信息（即直线）。利用在时频域上沿着所有可能的“直线”路径累积能量，即使是淹没在噪声中的微弱干扰直线，也能在其对应的参数空间中“积分”出一个强烈的峰值，从而被鲁棒地检测出来。

2. 步骤1：时频分析 (STFT)

首先，使用短时傅里叶变换（STFT）将接收到的差频信号$s_r(n)$转换到时频域，得到时频复矩阵$S_r(\zeta ,m)$：
$$S_r(\zeta ,m)=\sum _{n=-\infty }^{\infty }{s}_r(n)w(n-\zeta D)e^{-j2\pi \frac{m}{N}n}$$
其中 $w(n)$ 是窗函数，$\zeta$是时间索引，$m$是频率索引。继而，计算其功率谱图$P(\zeta ,m)=|S_r(\zeta ,m){|}^2$。这个功率谱图被视为一张“图像”输入到下一步。

3. 步骤2：功率加权霍夫变换 (Power-Weighted Hough Transform)

霍夫变换是图像处理中用于检测直线、圆等形状的经典算法。在标准霍夫变换中，一条直线许可用极坐标参数$(\rho ,\theta )$ 来定义。

本文对经典霍夫变换进行了关键修改，使其“功率加权”。传统的霍夫变换只是对二值图像上的点进行计数，而本文的方法则是对时频功率谱$P(\zeta ,m)$ 上的功率值进行累加。其累加器 $H_P$ 的定义为：
$$H_P(\rho ,\theta )=\sum _{(\zeta ,m)\in P}P(\zeta ,m)\delta (\zeta ,m)$$
这个公式的含义是：对于$(\rho ,\theta )$定义的每一条可能的直线，将该直线上所有时频单元$(\zeta ,m)$ 的功率 $P(\zeta ,m)$相加，得到累积分数$H_P(\rho ,\theta )$。通过这种方式，干扰信号的能量在$H_P$参数空间中被显著累积，形成了尖锐的峰值，而噪声和目标回波（水平线，$\theta \approx 0$通过）则不会。通过检测这些峰值，就能够极其鲁棒地定位出时频域中的干扰直线，即使在低信噪比（SNR）或低干扰噪声比（INR）下也能成功。

4. 步骤3：干扰抑制与AR模型恢复

一旦通过霍夫变换检测到干扰直线的位置，就将这些时频单元的数据视为“污染”并丢弃。

然而，这些被丢弃的单元（“空洞”）中可能也包含有用的目标信号。为了在去除干扰的同时最大限度地保留目标信息，论文使用了自回归（AR）模型进行信号恢复。该模型假设当前时域样本允许由其邻近的样本线性预测得出。对于时频谱中的每一个频率通道$m$，沿着时间轴$\zeta$建立AR模型：
$$S_{rec}(\tilde{\zeta },m)=\sum _{{\zeta }_n=1}^q{\Psi }_{{\zeta }_n}{S}_r(\zeta -{\zeta }_n,m)+ϵ$$
其中 $\Psi$是预测系数。利用干扰区域邻近的“干净”数据估计出$\Psi$，然后用它来“插值”填充被挖空的干扰区域，从而恢复出被掩盖的目标信号。最后，将这个“净化”后的时频谱$S_{rec}(\zeta ,m)$通过逆STFT（ISTFT）变换回时域$s_{rec}(n)$，得到无干扰的目标信号。

---

实验与结果分析

论文通过仿真和真实的硬件实验，将所提方法（Proposed）与七种其他主流方法（包括时域的Zeroing, CW, T-AR, IMAT, Wavelet和时频域的STFT-AR, CFAR-Burg）进行了全面对比。

评估指标

• CS (余弦相似度)：衡量恢复信号与原始信号的相似度，越接近1越好。
• EVM (误差向量幅度)：衡量恢复信号的失真，越小越好。
• PSLR (峰值旁瓣比) / ISLR (积分旁瓣比)：衡量频谱的旁瓣水平，值越低（负得越多）表示干扰抑制得越干净。

1. 仿真实验 (Simulation)

A. 无噪声仿真

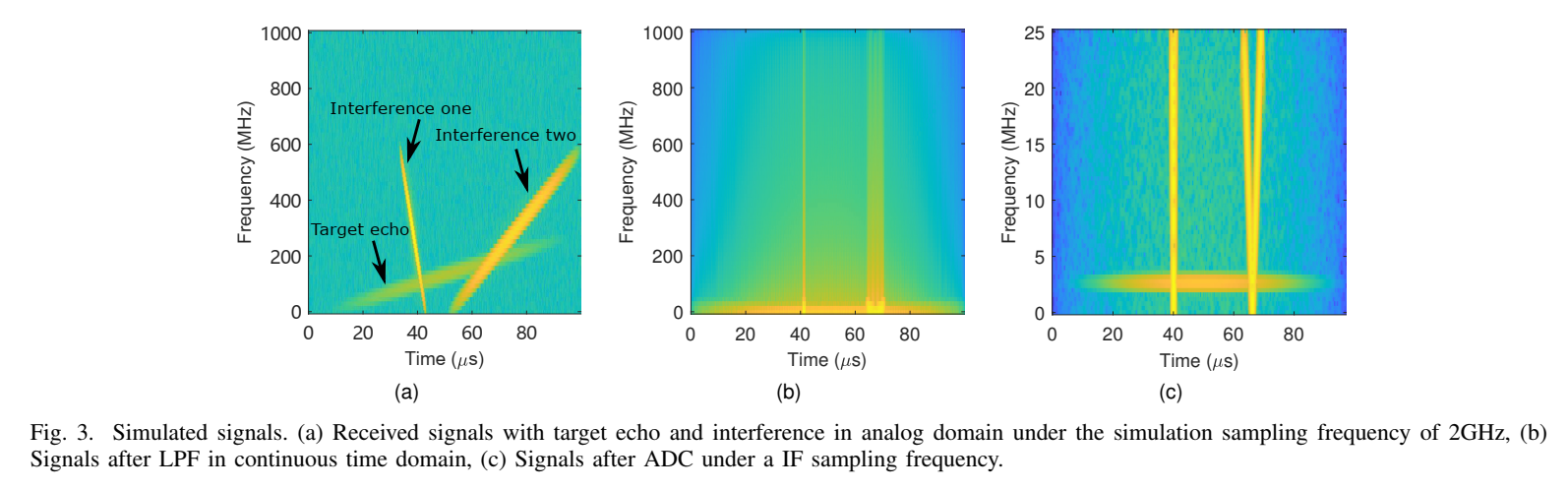
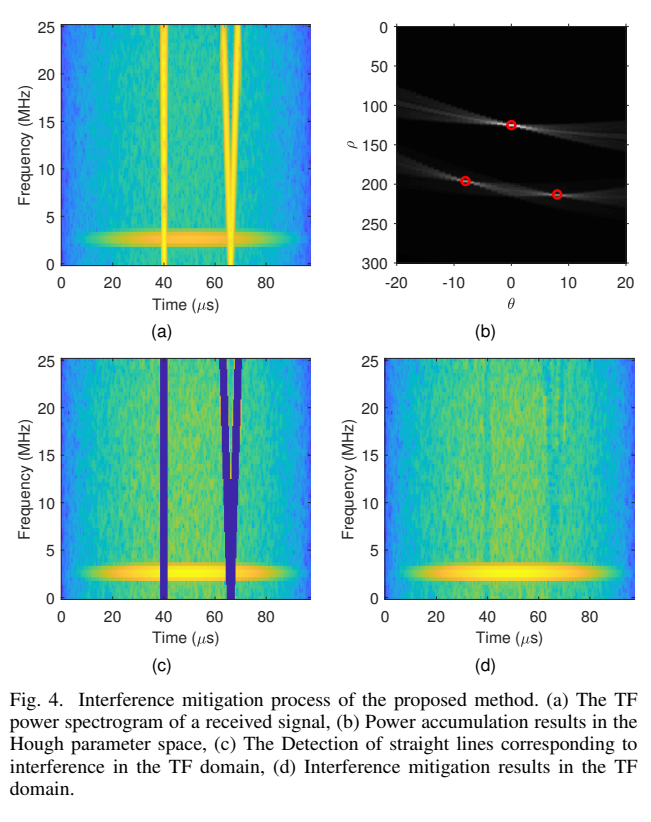
图3展示了仿真的原始信号、LPF输出和ADC采样信号。图4演示了所提技巧的完整流程：(a) 含有干扰（两条倾斜线）和目标（一条水平线）的时频谱；(b) 霍夫参数空间中的功率累积结果，清晰地显示出三个峰值（对应三条干扰线，其中两条在ADC采样后发生了折叠）；© 根据峰值检测到的干扰直线；(d) 干扰抑制和AR恢复后的干净时频谱，只留下了目标回波。

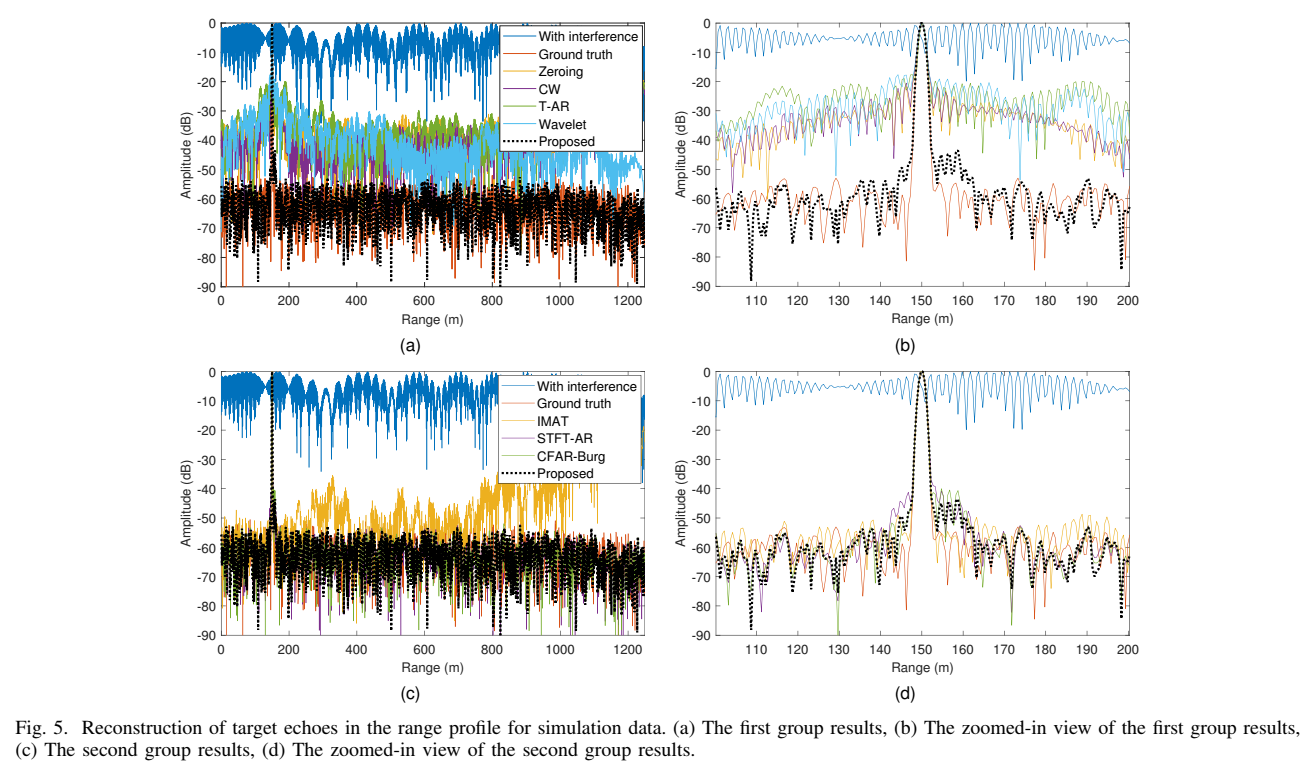
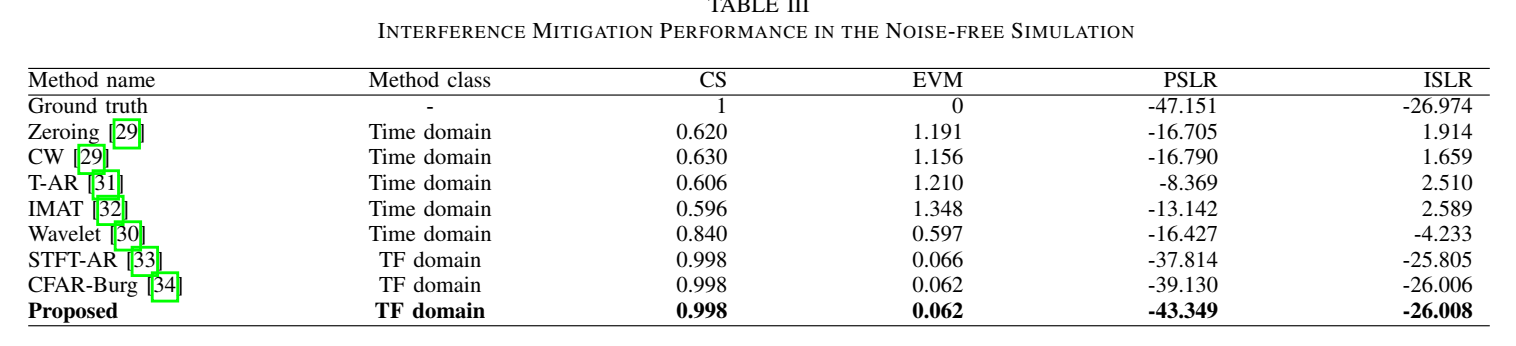
图5对比了各方法在无噪声下的距离剖面。结果显示，时频域方式（STFT-AR, CFAR-Burg, Proposed）的性能远超时域方法。所提方法（Proposed，黑色虚线）的旁瓣最低，几乎与“地面试验”（Ground truth）完美重合。表III的信息表明，所提途径的PSLR达到-43.349 dB，显著优于CFAR-Burg的-39.130 dB。

B. 不同信噪比（SNR）下的鲁棒性测试 (关键对比)

这是最关键的对比。实验模拟了弱干扰（干扰功率与目标功率相同），并在-30dB到10dB的SNR下进行测试。

图6的四张图（CS, EVM, PSLR, ISLR）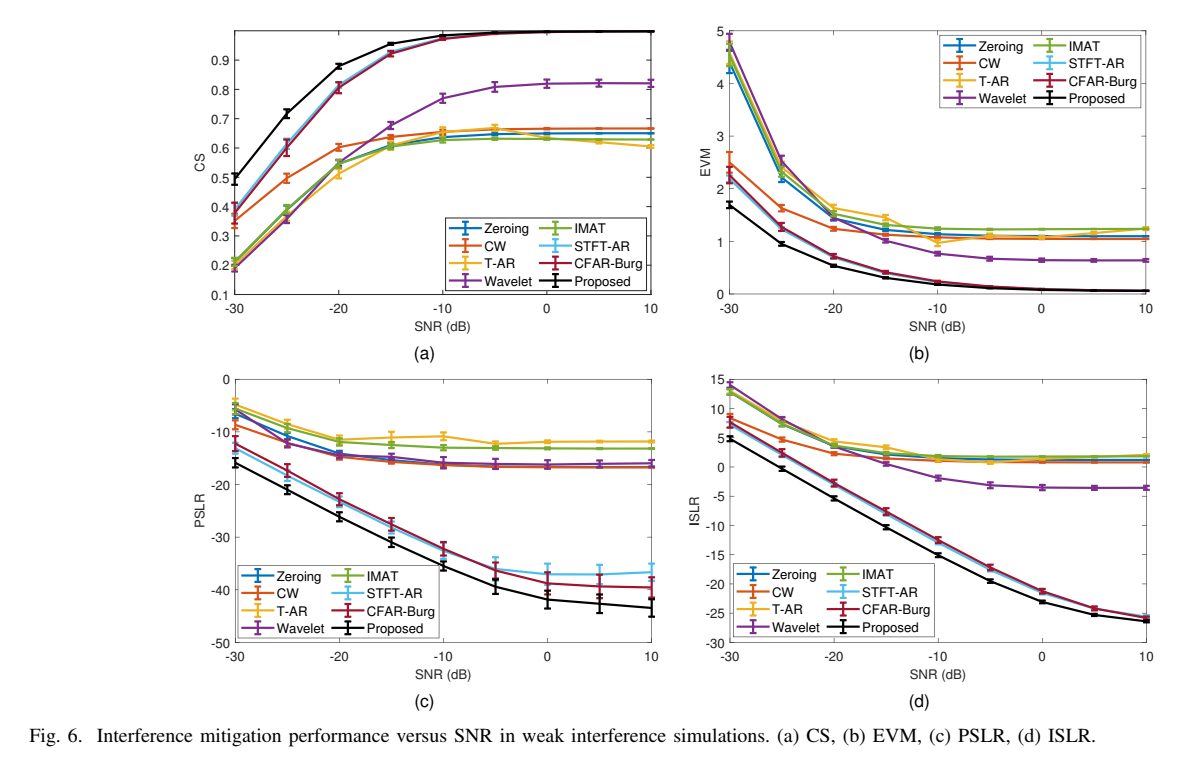

显示：

• 在低SNR（< -15dB）时，所有途径的性能都下降。
• 但STFT-AR和CFAR-Burg技巧的性能是急剧下降。
• 所提方法（紫色线）在极低的SNR下依然保持了出色的性能。例如，在-25dB的SNR下，所提方法的CS（余弦相似度）比其他两种TF方法高出约16% 。

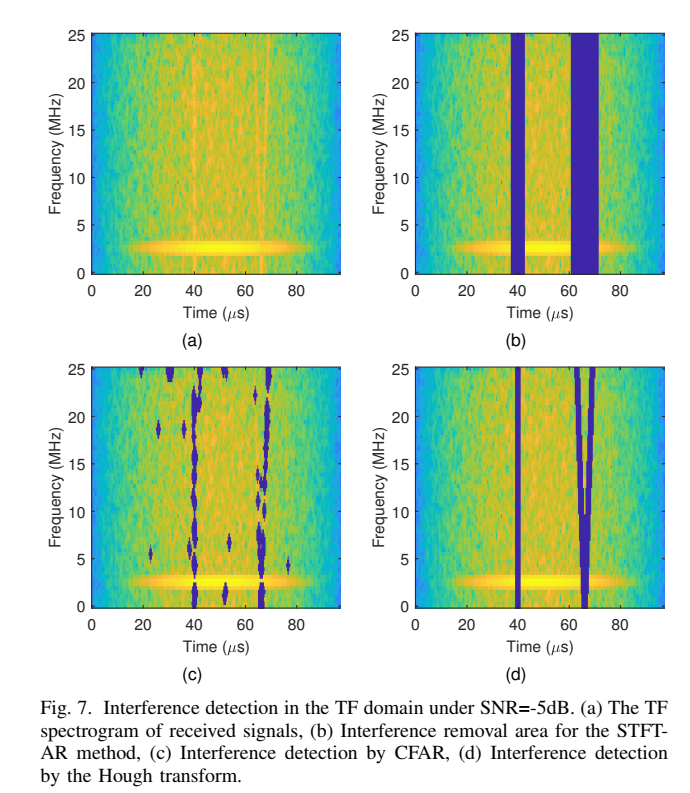
图7展示了原因。在-5dB的SNR下：

• © CFAR-Burg方法完全失效。它错误地将大量噪声识别为干扰（误报），并且未能检测到与目标回波重叠的干扰（漏报）。
• (d) 所提方法凭借其对“直线结构”的检测能力，无视噪声的干扰，准确地找到了两条干扰线。这证明了其在低SNR下的强大鲁棒性。

C. 运动目标仿真 (RD图)

此实验利用256个连续的Chirp来测试对运动目标的速度测量性能，这要求算法不仅能抑制干扰，还必须保持Chirp间的相位一致性。

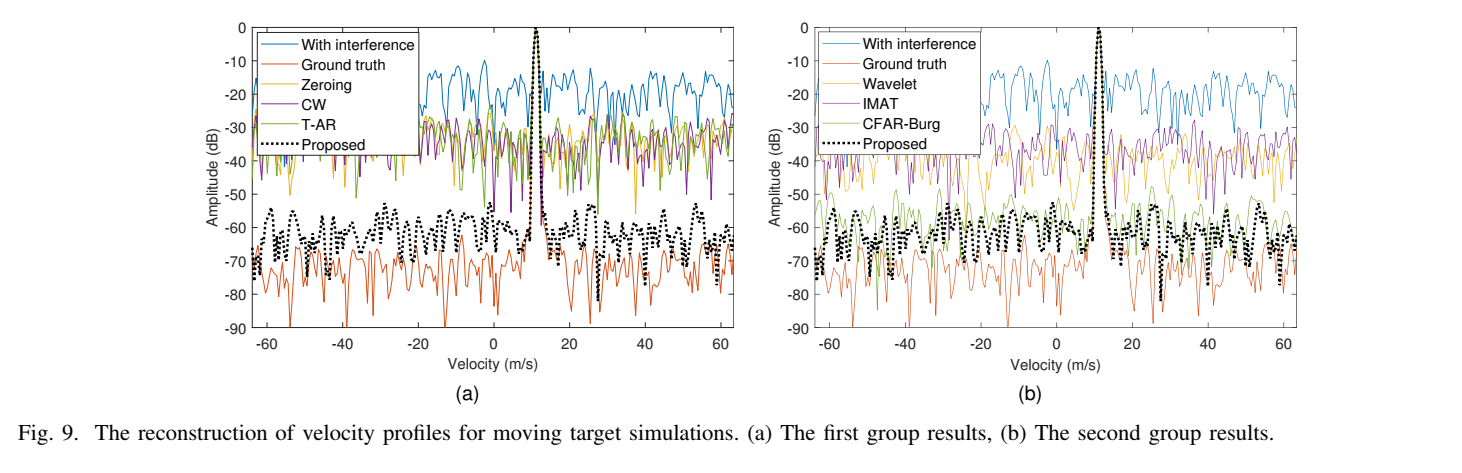
图8 和 图9 的结果：

• (b) 原始干扰数据中，目标（位于100m, 11m/s）完全被干扰淹没。
• ©-(g) 时域方法全部失败，无法恢复目标。
• (h) CFAR-Burg办法恢复了目标，但背景中仍有大量因误报和漏检导致的干扰残留，信噪比很差。
• (i) 所提方法完美地清除了干扰，得到了与(a)地面试验几乎一致的、极其干净的RD图。这证明该手段精确地抑制了干扰，同时完美地保持了信号的相位。
• 表IV的数据证实了这一点：所提方法在速度剖面上的PSLR（-52.459 dB）和ISLR（-38.637 dB最佳，遥遥领先于CFAR-Burg（-47.715 dB / -34.850 dB）。就是）指标上均

2. 真实场景实验 (Real Scenario)

实验使用了三台77GHz雷达，一台作为受害雷达，两台作为干扰源。

A. 静态目标 (角反射器)

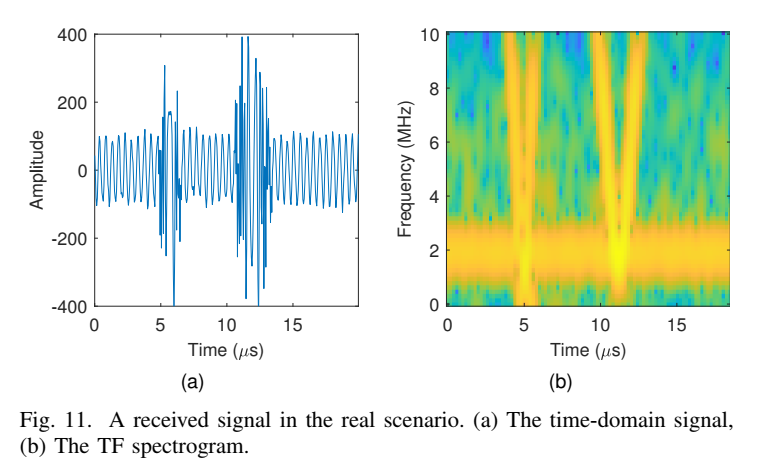
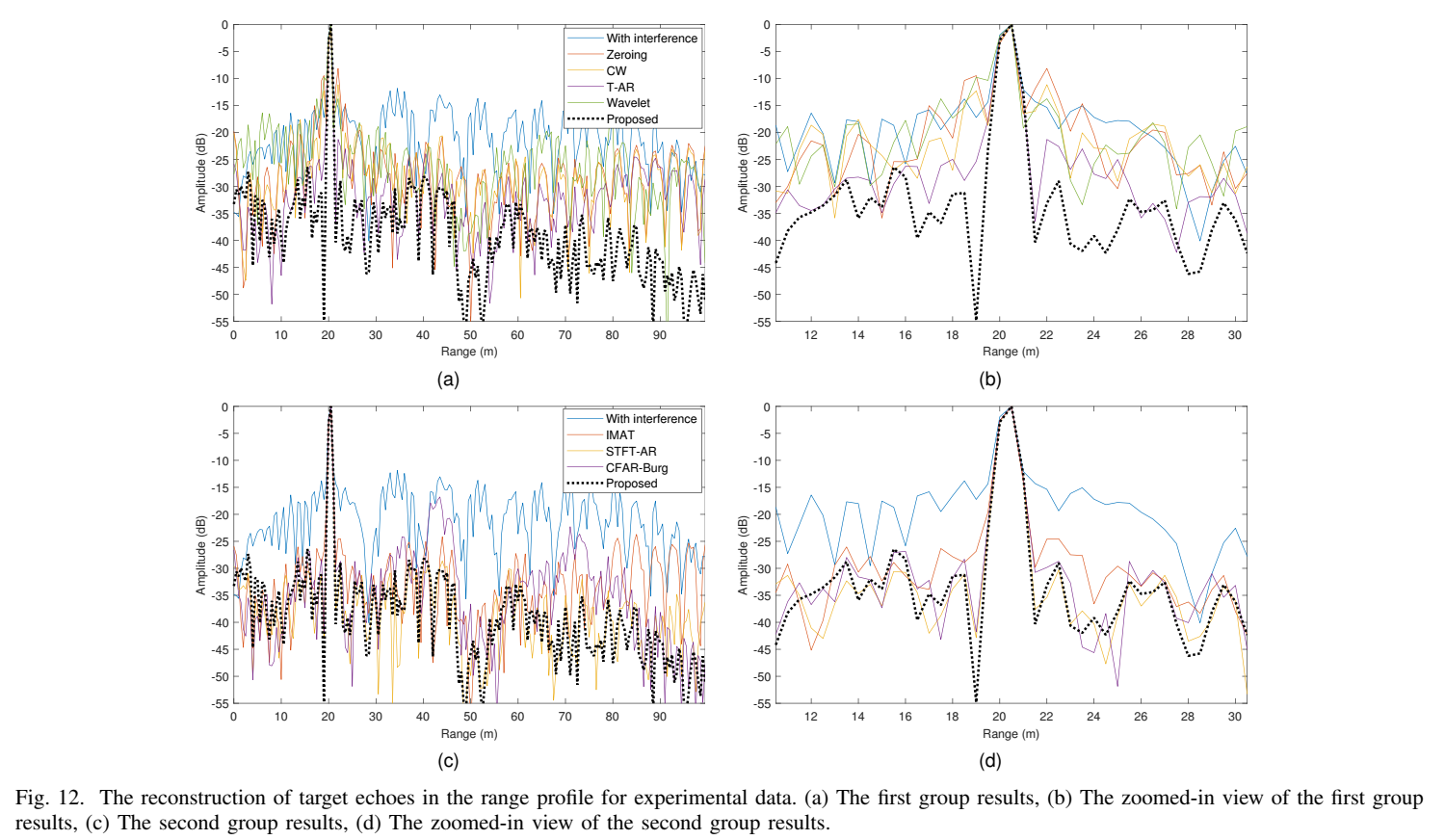
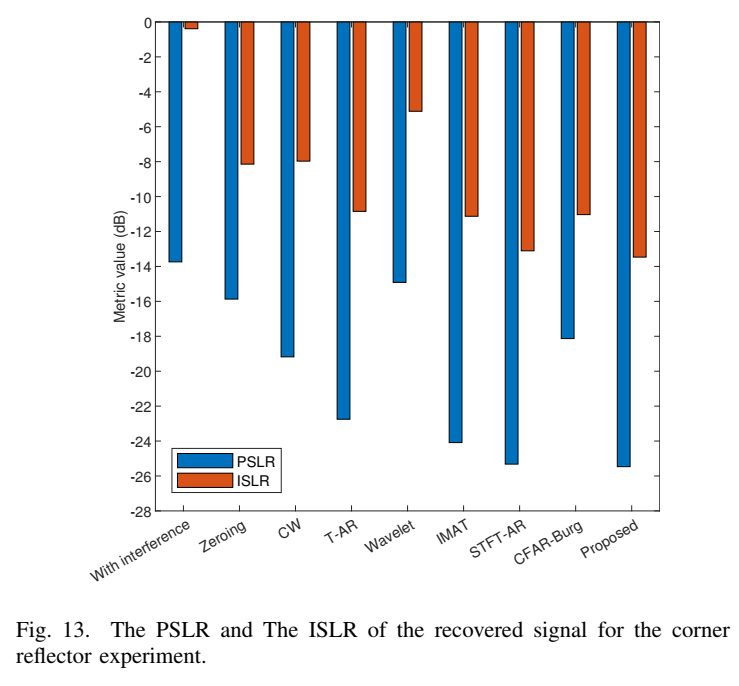
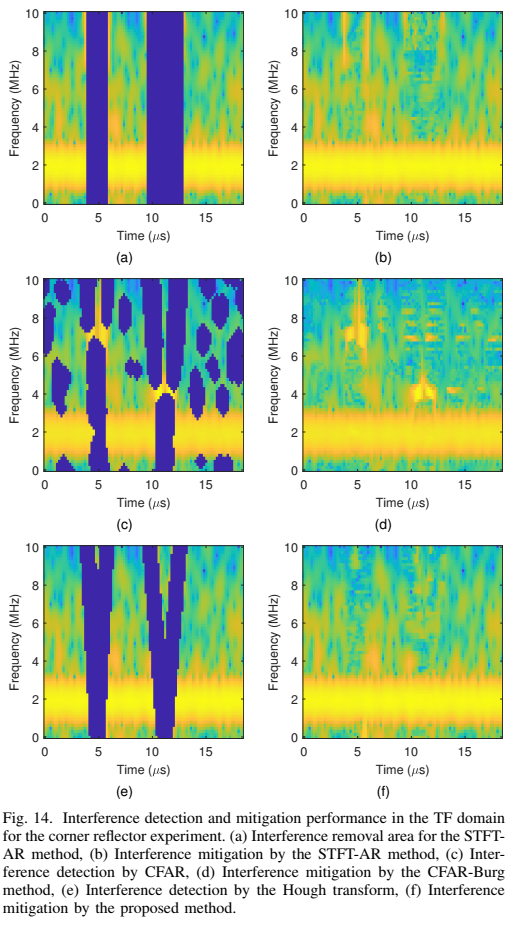
图11展示了真实采集的信号，其时频图(b)验证了模型的正确性：目标（角反射器）是水平线，而两个干扰是倾斜线。
图12 和 图13最好的。就是的结果表明，在真实数据上，所提方法的旁瓣抑制性能（PSLR/ISLR）同样
图14再次暴露了CFAR-Burg方法的缺陷：© 在真实场景的密集干扰下，CFAR的检测器“失效”了，导致干扰漏检。而 (e) 所提技巧利用结构信息，准确地定位了干扰。

B. 行人实验 (最关键的展示)

一个极具挑战性的场景：在两个强干扰源存在的情况下，检测一个在30-40米处行走的就是这弱目标（行人）。

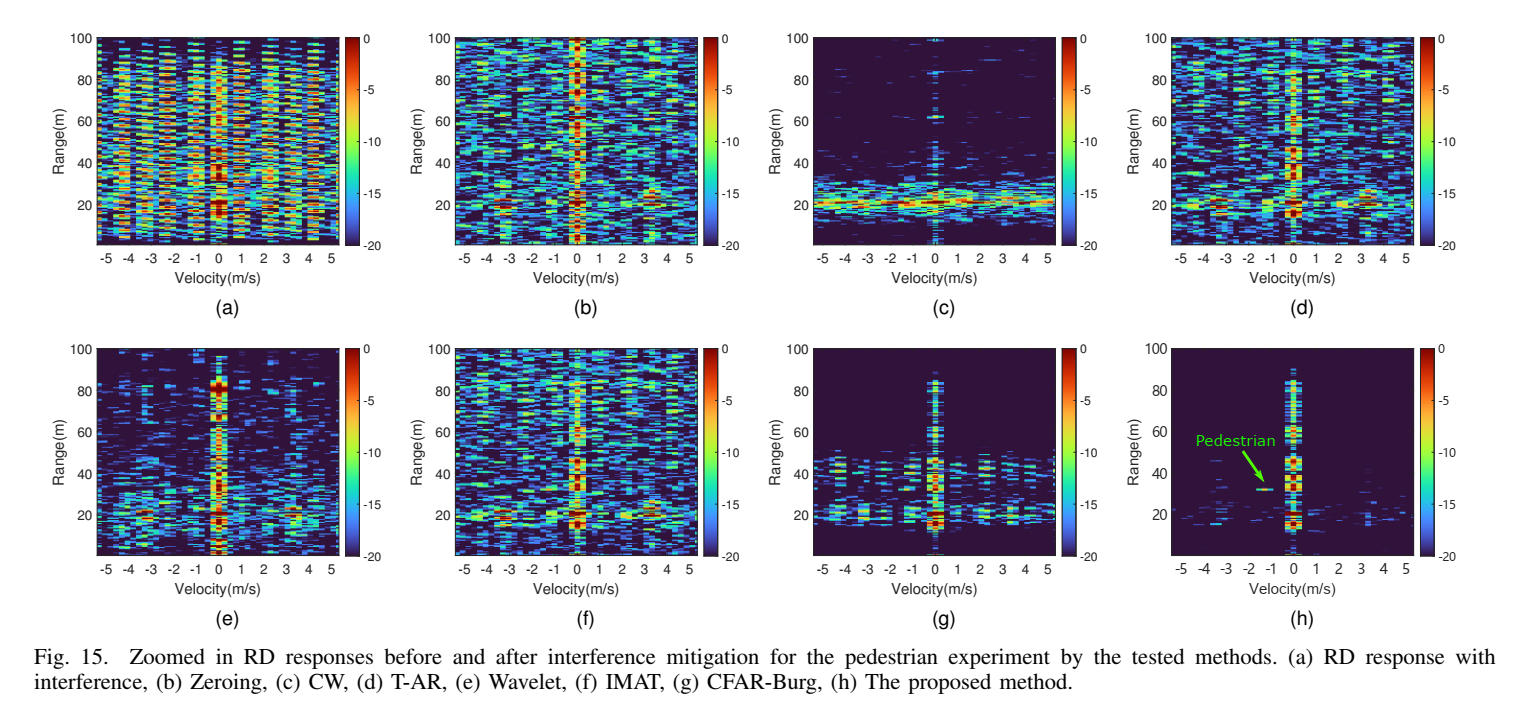
图15是这篇论文最关键的结果：

• (a) 在原始RD图中，干扰极强，行人完全不可见。
• (b)-(f) 所有时域技巧全部失败，无法检测到行人。
• (g) CFAR-Burg办法由于干扰漏检，几乎检测不到行人，目标淹没在残留的干扰中。
• (h) 所提方法成功地抑制了所有强干扰，清晰地揭示了行人的位置和速度（图中标注的“Pedestrian”）。

---

讨论与结论

算法复杂度 (Runtime)
表VI相互独立的，因此就是显示，所提途径（560.2ms）是所有方法中计算时间最长的，显著慢于CFAR-Burg（490.8ms）和时域方法（~5-15ms）。这是因为霍夫变换需要在二维参数空间中进行搜索和累加，计算量巨大。但作者指出，霍夫变换的计算网格非常适合并行化处理（例如使用FPGA或GPU），在未来的实际车载芯片部署中，其运行时间许可被大幅缩短。

结论
本文分析了FMCW雷达干扰在解啁啾后于时频域上呈现的线性结构特征。基于此，提出了一种功率加权霍夫变换方法，它不依赖于干扰的幅度，而是通过在时频域累积干扰的结构功率来鲁棒地检测和定位干扰。结合AR模型进行信号恢复，该方法被证明在低SNR、低INR和干扰密集等极端条件下，其性能和鲁棒性均显著超越了现有的时域和时频域技巧。最重要的是，在真实的行人检测实验中，该途径是唯一能够从强干扰中成功恢复弱目标的算法。

---

附录：数学推导

如何从混频器推导出来的。这里补充这一推导。就是本文在正文中给出了信号模型和差频公式（Eq. 11, 12），但省略了它们

附录A: 目标回波差频 ($f_b$) 推导

1. 信号定义
根据论文 Eq. 1 和 Eq. 5，我们只看其相位项（忽略幅度和初始相位）：

• 参考信号相位：${\phi }_t(t)=2\pi (f_{c}t+\frac{1}{2}k{t}^2)$
• 回波信号相位：${\phi }_e(t)=2\pi (f_c(t-\tau )+\frac{1}{2}k(t-\tau {)}^2)$

其中 $\tau =2R/c$是双程延迟。

2. 混频（Dechirp）
混频器将两个信号相乘。使用积化和差公式$\cos (A)\cos (B)=\frac{1}{2}[\cos (A+B)+\cos (A-B)]$：

• 和频项 ($A+B$) ：${\phi }_t(t)+{\phi }_e(t)$。其频率约为$2f_c$（例如 154 GHz），会被低通滤波器（LPF）完全滤除。
• 差频项 ($A-B$) ：${\phi }_b(t)={\phi }_t(t)-{\phi }_e(t)$。这是利用LPF的差频信号。

3. 推导差频相位${\phi }_b(t)$
$${\phi }_b(t)=2\pi \left[(f_{c}t+\frac{1}{2}k{t}^2)-(f_c(t-\tau )+\frac{1}{2}k(t-\tau {)}^2)\right]$$
展开 $t$ 的相关项：
$${\phi }_b(t)=2\pi \left[(f_{c}t-f_{c}t+f_c\tau )+\frac{1}{2}k(t^2-(t^2-2t\tau +{\tau }^2))\right]$$
$${\phi }_b(t)=2\pi \left[f_c\tau +\frac{1}{2}k(2t\tau -{\tau }^2)\right]$$
$${\phi }_b(t)=2\pi \left[(k\tau )t+(f_c\tau -\frac{1}{2}k{\tau }^2)\right]$$

4. 求解瞬时频率$f_b$
瞬时频率是相位对时间的导数除以$2\pi$：
$$f_b(t)=\frac{1}{2\pi }\frac{d{\phi }_b(t)}{dt}$$
$$f_b(t)=\frac{1}{2\pi }\frac{d}{dt}\left(2\pi \left[(k\tau )t+(f_c\tau -\frac{1}{2}k{\tau }^2)\right]\right)$$
$$f_b(t)=k\tau$$

一个就是这证明了目标回波的差频恒定频率$k\tau$，与论文中的Eq. 11完全一致。式中的$f_c\tau -\frac{1}{2}k{\tau }^2$是一个常数，对应论文Eq. 13中的恒定相位${\Phi }_b$。

附录B: 干扰信号差频 ($f_{bi}$) 分析

1. 信号定义

• 参考信号相位：${\phi }_t(t)=2\pi (f_{c}t+\frac{1}{2}k{t}^2)$
• 干扰信号相位：${\phi }_i(t)=2\pi (f_{ci}(t-{\tau }_i)+\frac{1}{2}{k}_i(t-{\tau }_i{)}^2)$

2. 混频与推导差频相位${\phi }_{bi}(t)$
同样，我们只看差频项${\phi }_{bi}(t)={\phi }_t(t)-{\phi }_i(t)$：
$${\phi }_{bi}(t)=2\pi \left[(f_{c}t+\frac{1}{2}k{t}^2)-(f_{ci}(t-{\tau }_i)+\frac{1}{2}{k}_i(t-{\tau }_i{)}^2)\right]$$
展开 $t$ 的相关项：
$${\phi }_{bi}(t)=2\pi \left[f_{c}t+\frac{1}{2}k{t}^2-(f_{ci}t-f_{ci}{\tau }_i+\frac{1}{2}{k}_i(t^2-2t{\tau }_i+{\tau }_i^2))\right]$$
$${\phi }_{bi}(t)=2\pi \left[(f_c-f_{ci})t+(\frac{1}{2}k-\frac{1}{2}{k}_i)t^2+(k_i{\tau }_i)t+(f_{ci}{\tau }_i-\frac{1}{2}{k}_i{\tau }_i^2)\right]$$
整理为 $t$的二次多项式：
$${\phi }_{bi}(t)=2\pi \left[\frac{1}{2}(k-k_i)t^2+(f_c-f_{ci}+k_i{\tau }_i)t+(\text{Constant terms})\right]$$

3. 求解瞬时频率$f_{bi}$
$$f_{bi}(t)=\frac{1}{2\pi }\frac{d{\phi }_{bi}(t)}{dt}$$
$$f_{bi}(t)=\frac{1}{2\pi }\frac{d}{dt}\left(2\pi \left[\frac{1}{2}(k-k_i)t^2+(f_c-f_{ci}+k_i{\tau }_i)t+\dots \right]\right)$$
$$f_{bi}(t)=(k-k_i)t+(f_c-f_{ci}+k_i{\tau }_i)$$

分析：
这个推导结果表明，干扰差频$f_{bi}(t)$ 是时间 $t$ 的线性函数（即LFM信号），其斜率为$(k-k_i)$。这在物理上证实了论文的核心前提。

（注：此推导结果$f_{bi}=(f_c-f_{ci}+k_i{\tau }_i)+(k-k_i)t$ 与论文中的 Eq. 12$f_{bi}=(f_c-f_{ci}+k_i{\tau }_i)+\frac{1}{2}(k-k_i)t$在系数上存在$\frac{1}{2}$的差异，这似乎是原文Eq. 10 和 Eq. 12之间的一个常见笔误。然而，无论斜率是$(k-k_i)$ 还是 $\frac{1}{2}(k-k_i)$，其关键物理特性——信号是一个瞬时频率随时间$t$线性变化的LFM信号——是完全成立的，这也是本文算法所依赖的根本基础。）