实用指南：如何理解Transformer的自注意力机制

本章博客主要分成三部分，第一部分包括第一章和第二章，是一些必要的数学知识回顾和概念学习；第二部分包括第三章和第四章，主要介绍了Transformer的核心计算以及对应的单头和多头计算示例；第三部分即第五章，主要是视觉领域的Transformer.

主要目的是为了让自己将一些数学原理和Transformer的核心处理方法可以形成自恰，不求说非常深入地了解掌握Transformer，但求为以后能更深入了解这个伟大的算法铺一下路。

1.向量点积

几何意义：通过投影的方法来计算：

$a·b=||a||·||b||·cos\theta$

代数意义：通过向量的坐标进行计算：

$a·b=a_{1}·b_{1}+a_{2}·b_{2}+...+a_{n}·b_{n}$

这里举个例子来感受下点积的几何和代数计算：计算向量 a=( $\sqrt{3}$ ,1)和 b=(1, $\sqrt{3}$ ) 的点积，向量 a 与x轴夹角30°，向量 b 与x轴夹角60°

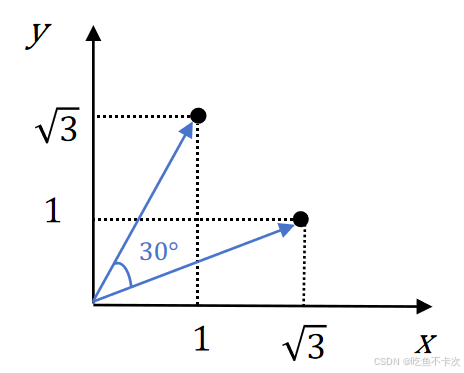
代数方法计算

$a·b=a_{1}·b_{1}+a_{2}·b_{2}=\sqrt{3} \times 1+1\times \sqrt{3}=2\sqrt{3}$

几何方法计算

$\left \| a \right \|=\sqrt{(\sqrt{3})^{2}+1^{2}}=\sqrt{3+1}=2$

$\left \| b \right \|=\sqrt{1^{2}+(\sqrt{3})^{2}}=\sqrt{1+3}=2$

两向量夹角：θ = 60° - 30° = 30°

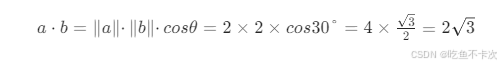
需要注意的点：

1.点积的值范围从 −∞ 到 ∞，具体值取决于向量的模长和夹角。

2.可以通过余弦相似度来表示两个向量的相似度，余弦相似度的范围是[−1,1]，其中1表示两个向量方向完全相同，相似度最高；-1表示两个向量方向完全相反，相似度最低；0表示两个向量正交，没有相似性。

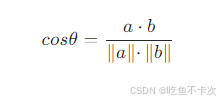
比如在上面例子中，将值代入可求得这两个向量的余弦值：

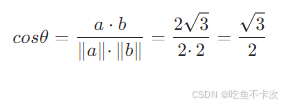
2.矩阵乘法

2.1矩阵左乘

我们在学习线性代数的时候，一般都是给定一个向量 $a=[1,1]^{T}$ ,一个矩阵A=[[1,1],[0,1]],然后通过下面这种方式来计算向量和矩阵的乘法，最后得到新的向量 $[2,1]^{T}$

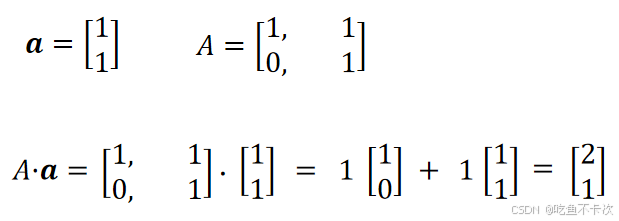
那么矩阵左乘做了什么才让向量a从 $[1,1]^{T}$ 变成了 $[2,1]^{T}$ 呢？具体可以去b站找3blue1brown的《线性代数的本质》课程来看，我这里只是简单介绍一下矩阵变换的过程：

（1）矩阵AAA相当于构建了一个新的坐标系 $X'OY'$ ，从矩阵A的第一列看，x轴的基向量没变化，还是 $[1,0]^{T}$ ；从矩阵AAA的第二列看，y轴的基向量从 $[0,1]^{T}$ 变成了 $[1,1]^{T}$ ,相当于变换后的坐标系 $X'$ 轴和 $Y'$ 轴夹角变成了45°

（2）那么在这个新坐标系 $X'OY'$ ′中，也存在顶点为（1，1）的向量，不过映射回坐标系 $XOY$ 中就不是（1，1）,而是（2，1）,也就是我们通过矩阵左乘计算得到的结果。

（3）也就是说在坐标系 $XOY$ 中，顶点（1，1）经过矩阵A的线性变换之后变成了顶点（2，1），换句话来说，在 $XOY$ 坐标系的顶点（1，1）和 $X'OY'$ 坐标系中的顶点（1，1）通过矩阵A的线性空间变化，使得 $X'OY'$ 坐标系中的顶点（1，1）映射回 $XOY$ 坐标系就是点（2，1）

那么线性变换有什么用呢？我觉得下面这句话说得特别好，引用自卢菁老师的《速通深度学习数学基础》P18：对于向量x,基于新的需求，我们可能需要从新的角度进行观测，新的角度有可能将某些特征放大，同时忽略一些无关因素。

比如在这里，我们可以明显观察到经过线性变换后的顶点（2,1）相比之前距离原点（0,0）的距离更远了，或许在这个观测角度下，可以放大某些特征，可以让某些特征更加明显。

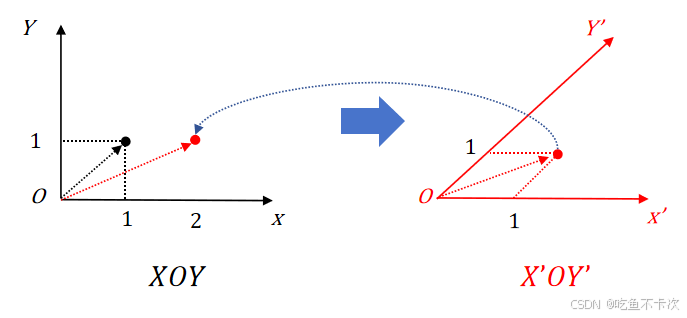
2.2矩阵右乘

其实这个和矩阵左乘是一样的，只不过向量aaa从列向量变成了行向量 $[1,1]$ ，矩阵A也进行了转置变成了

$[[1,0], [1,1]]$ ，并且最后得到的结果也是行向量 $[2,1]$ ，矩阵右乘，矩阵右乘，矩阵右乘 $a\cdot ·A$ 如下所示。

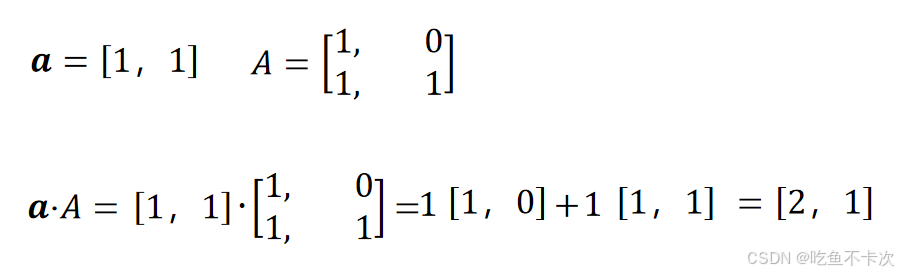
在深度学习中，向量aaa一般就是输入值，矩阵A是可以模型需要学习更新的权值，结合前面说的，经过矩阵变换，从新的角度进行观测，新的角度有可能将某些特征放大，同时忽略一些无关因素。这就是线性代数在深度学习中的实际运用。

3.自注意力机制

3.1相似度

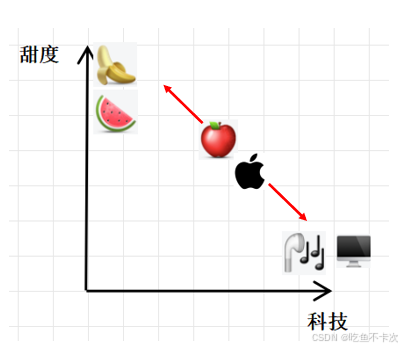
假设现在有一个二维空间，分别表示科技量和甜度，那么如下图可知，电脑、蓝牙耳机的科技量拉满，甜度基本为0；而香蕉和西瓜的甜度拉满，科技量也基本为0；

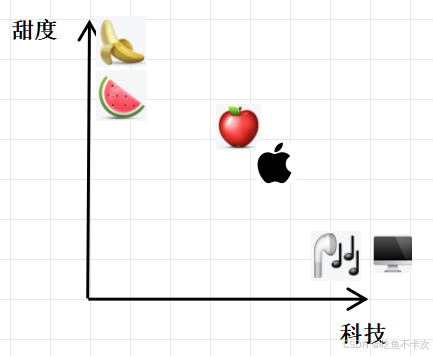
假设香蕉的向量记为fruit1=(0.0005,90)，西瓜的向量记为fruit2=(0.001,80)，假设电脑的向量记为machine1=(95,0)，耳机的向量记为machine2=(60,0).

(1)水果间的向量点积：

即香蕉和西瓜的向量点积为fruit1·fruit2=0.0005·0.001+90·80=7200.0000005

(2)科技产品间的向量点积：

即电脑和耳机的向量点积为machine1·machine2=95·60+0·0=5700

(3)水果和科技产品间的向量点积：

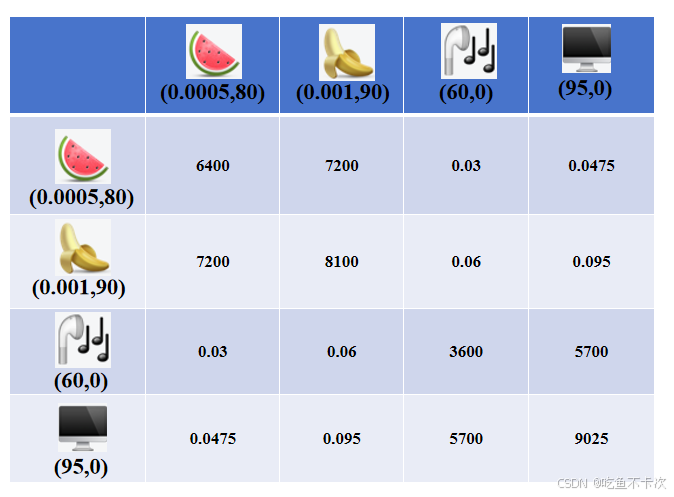
比如香蕉和电脑的向量点积 fruit1·machine1=0.0005·95+90·0=0.0475，这样一下子就能看出来区别了，香蕉和电脑的相似度明显低于水果间的点积，也明显低于科技产品间的点积，具体可以见下表。

(4)自身的向量点积：

比如电脑和电脑的向量点积machine1·machine1=95·95+0·0=9025，是当前相似度最大的；

再比如西瓜和西瓜的向量点积fruit2·fruit2=0.001·0.001+80·80≈6400，此时我们发现西瓜自身的相关度还没有香蕉和西瓜的向量点积大，不应该自身的向量点积是最大的吗？

这里就是前面说到的点积的大小取决于向量的模长和夹角，在这里西瓜自身的夹角为0，已经是最相似的一个角度，但是模长没有香蕉的大，所以自身点积小于香蕉和西瓜的点积。

但如果下表使用余弦相似度（cosθ）表示的话，那么自身的相似度是最大的，即对角线都为1。

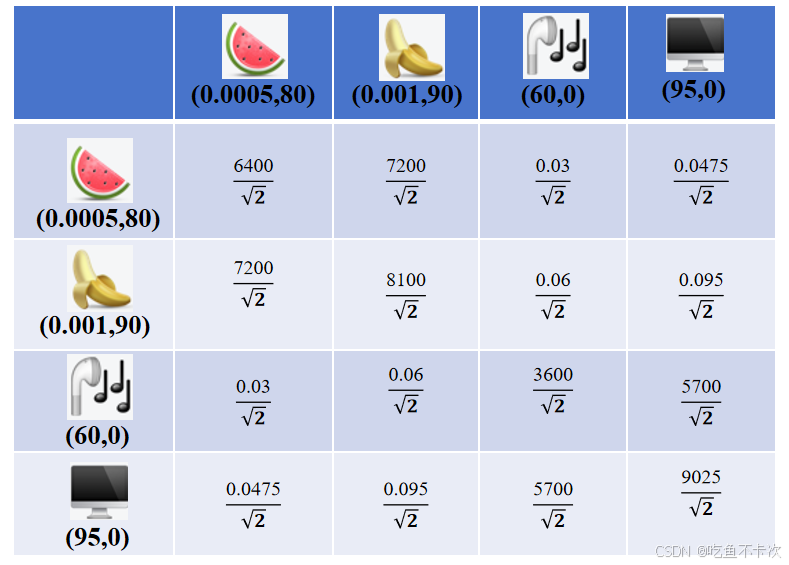
在Transformer中不使用余弦相似度来表示每个token之间的相似度，而是使用向量的点积获取原始注意力分数，再通过除以向量维度的平方根（ $\sqrt{d_k}$ ）进行缩放，从而得到最终的相似度表示，如下表所示。

这里需要注意以下几点：

1.没有使用余弦相似度来表示token之间的相似度是为了保留每个token的模长信息，也是为了充分学习到当前token和其他token的相似度信息，而不是为了每次都得到自身的相似度最大的这个基本事实。

2.除以向量维度的平方根（ $\sqrt{d_k}$ ）这样做是为了避免向量维度过高，导致最后计算的向量点积结果过大，也是为了避免一些点积结果太大，容易导致经过softmax后很多值变成0，不利于构成权重矩阵。

3.所谓的token就是这些物品向量化后的结果，在这里就是二维的向量，分别为[0.0005,80],[0.001,90],[60,0],[95,0]，那么tokens就是这些向量的拼接，每一行代表一个token，每一列代表一个维度信息；（这里再插一嘴，NLP任务中的token是指句子分词后的向量表示，CV任务的token是指切分成小图之后的向量表示）

最后需要通过softmax来输出当前token对每个token的注意力，由于上面的例子的值过于极端，经过softmax后自身的注意力权重变成1，不利于举例说明transformer中的相似度，所以下表经过softmax后的数值是重新编的，主要用来理解完整过程的，softmax的计算公式如下：

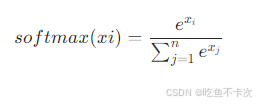
从下表可以看到经过softmax之后，每行的和均为1，以第一行为例，站在西瓜的角度，分配0.57的注意力权重给西瓜，0.40的注意力权重给香蕉，0.01的注意力权重给耳机以及0.02的注意力权重给电脑。

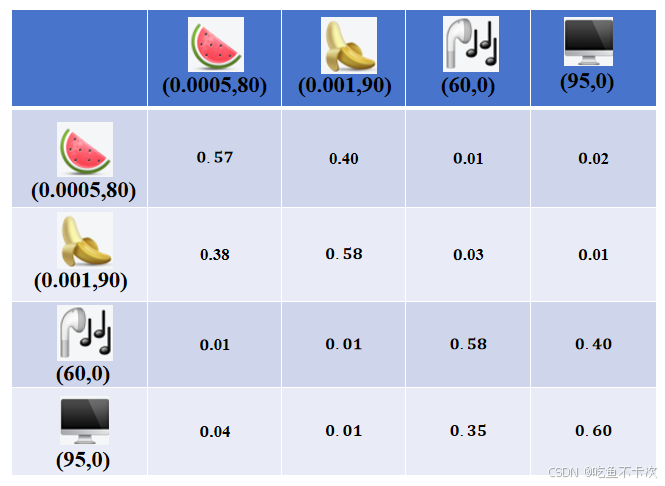
根据上表中的权重矩阵来更新每个token的值，如下所示

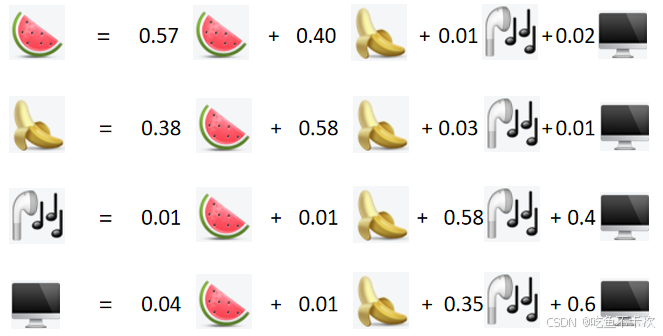
以西瓜和香蕉为例子来计算更新后的向量，如下所示，其中，西瓜和香蕉经过自注意力计算后变成(2.5,81.6)和(2.75,82.6)，这两个向量相较之前，在二维空间上的欧氏距离更小了，说明注意力机制拉近了相近的两个token。

西瓜：0.57*(0.0005,80)+0.40*(0.001,90)+0.01*(60,0)+0.02*(95,0)
=(0.000285,45.6)+(0.00040,36)+(0.6,0)+(1.9,0)
=(2.5,81.6)
香蕉：0.38*(0.0005,80)+0.58*(0.001,90)+0.03*(60,0)+0.01*(95,0)
=(0.00019,30.4)+(0.00058,52.2)+(1.8,0)+(0.95,0)
=(2.75,82.6)

如果使用矩阵乘法表示的话就是如下所示：

另外还需要注意一点，就是尽管科技产品类和水果类的相关性很小很小，最后经过softmax后也会分配一个权重，哪怕这个权重也是很小很小的值，所以我个人的理解是自注意力计算最直接的结果就是让相似的token联系更紧密，但是也会分配适当的权重给一些不相关的token，是为了让每个token的表达都更加丰富和具有全局感知能力。

因此“苹果”在上下文中作为可以吃的水果时，经过多次自注意力计算，将逐渐向水果类靠近（即左上角区间）；当“苹果”在上下文中作为使用的手机时，经过多次自注意力计算，将逐渐向科技产品类靠近（即右下角区间）。

3.2Self-Attention

前面在计算相似度权重并更新值的过程，可以使用下面这条公式表示：

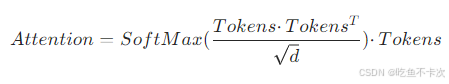
不过，我们观察到这样会存在一点问题：（1）Tokens作为输入，需要身兼三职，除了要作为相似度权重计算的查询者和被查询者，还要作为输出值的基准值；（2）整个Attention计算过程没有可学习的参数，也就没有梯度更新优化整个过程。

那么为了解决这两个问题：

引入了 $W_{q}, W_{k}, W_{v}$ ,使得 $Q=Tokens·W_{q}, K=Tokens·W_{k}, V=Tokens·W_{v}$ ，然后通过下面这条式子来计算Attention，注意，这里的d表示的Q/K/V的维度数，也就是列数:

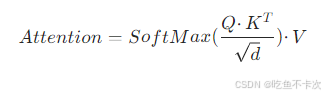
这样子就可以使得tokens有了Q、K、V三个分身可以各司其职，并且 $W_{q}, W_{k}, W_{v}$ 这三个矩阵是可学习的，学习找到一个新的角度去将某些特征放大，同时忽略一些无关因素。

举个例子，现在有一句话：I like to eat banana and "Apple"，also like to play computer game and use "Apple" phone.

对于我们人类来说很明显，第一个“Apple"指代的是水果，第二个”Apple"指代的是手机。

那么如何通过self-Attention注意力机制也学习到这一点呢，换句话说经过self-Attention后，第一个“Apple"对于banana的权重大于对于computer的权重，使得第一个“Apple”和banana更靠近；同理，也要使得第二个“Apple"和computer更靠近。这一步也就是我们在3.1所说的内容，通过计算相似度并更新每个tokens的值。

那么如何让这个过程更快收敛并且实现更好的效果呢，就需要引入 $W_{q}, W_{k}, W_{v}$ ,

首先知道什么时候用到 $W_{q}, W_{k}, W_{v}$ ，这三个矩阵是用在计算QKV的，如下所示：

其中Q和K是用来计算相似度并生成权重矩阵的，基于“相似的token相似度更大，不相似的token相似度更小”的任务下， $W_{q}$ 和 $W_{k}$ 的作用就是为了将水果类和科技产品类在新的坐标系下距离更远，换句话说，就是模型在优化的过程中不断地去更新 $W_{q}$ 和 $W_{k}$ 这两个值，从而让水果类和科技产品类这两类变得更好区分，从而在计算相似度的时候更能够体现出哪些”相似“，哪些”不相似“，可以结合下面的示图理解。

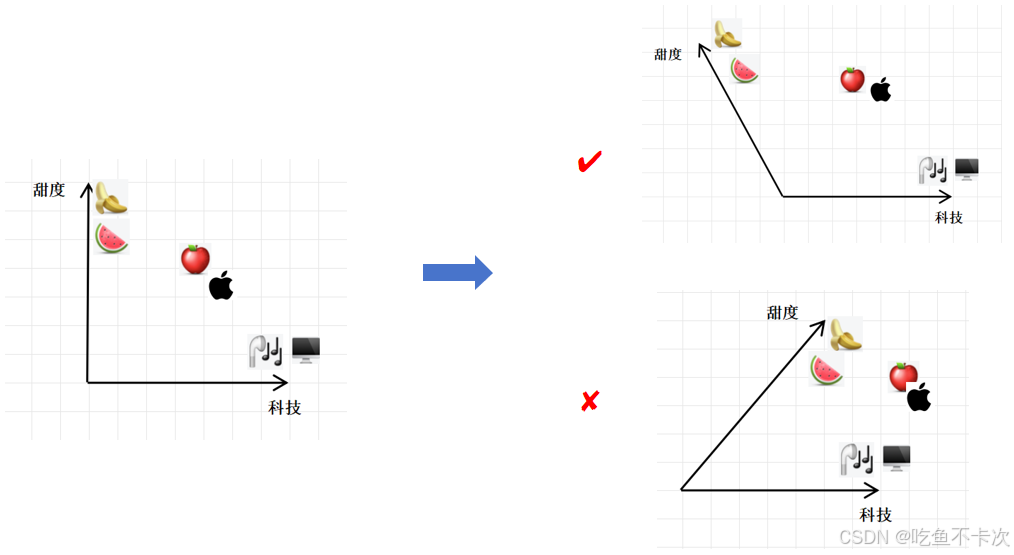
V是最后进行权重计算的基准值，为啥基准值不直接使用原始的tokens，而是使用和 $W_{v}$ 矩阵相乘后的结果呢？

同样的，如果使用原始的tokens，那么前面计算的注意力权重只是在决定“复制”多少原始的、未经处理的语义信息，这样就变成了简单的计算过程了，并不包含学习优化过程，这样是没有意义的；

而tokens和 $W_{v}$ 矩阵相乘，还是那句话，加入了可学习的矩阵，可以根据任务的不同找到一个新的角度去将某些特征放大，同时忽略一些无关因素。例如，对于情感分析任务， $W_{v}$ 矩阵可能会放大与情感相关维度的语义信息，弱化其他无关维度的信息。

3.3Multi-Head Attention

在了解单头注意力机制后，现在再来看多头注意力机制，这两者其实就一点不相同，就是从单头变成了多头，那么在哪里多头呢？

还记得前面说的，通过 $W_{q}, W_{k}, W_{v}$ 这三个可学习的矩阵，去找到一个新的角度去将某些特征放大，同时忽略一些无关因素，这个就是self-Attention即单头注意力机制的核心；

现在假设通过多组（ $W_{q}, W_{k}, W_{v}$ ）这样的可学习的矩阵，是不是就可以找到多个角度去将某些特征放大了，事实上确实是这样，这种方式叫做Multi-Head Attention多头注意力机制；

当然multi-Head Attention也存在其他变体，主要是介绍这种：即还是通过一组（ $W_{q}, W_{k}, W_{v}$ ）这样的可学习的矩阵，和单头注意力机制一样计算得到Q/K/V；然后对Q/K/V的列拆分成heads组，每组有d/heads列，即每个token包含d/heads个维度；然后再对heads个组分别计算注意力权重并更新每个组的V值；最后将heads个V值进行拼接得到多头注意力机制的计算结果。

这样的表述是很枯燥抽象的，可以结合下一章的计算示例来理解该过程。

4.计算示例

4.1self-Attention

这里就不以前面的香蕉，西瓜，耳机，电脑为例了，以维度为4作为例子说明计算过程， $W_{q}, W_{k}$ 是和token维度相同的矩阵，即矩阵的列数为4，所以矩阵就是4x4的矩阵（当然也可以对输入的token进行升维或者降维，这里是保持原始的维度）;

具体计算过程如下所示：

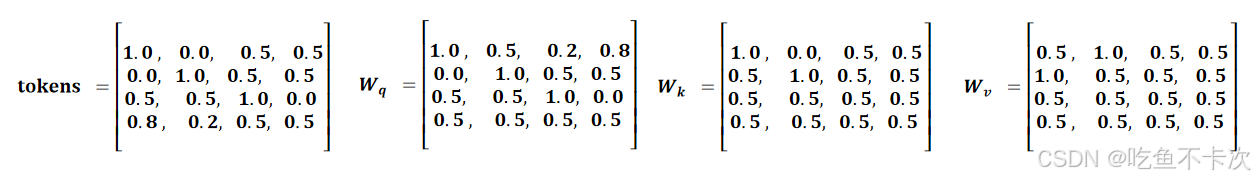
（1）首先通过矩阵乘法，可以计算得到Q、K、V的值：

（2）然后计算权重：

（3）最后计算输出结果为：

4.2Multi-Head Attention

继续以4.1的为例子，设置heads=2，即分成两个头，计算过程如下所示：

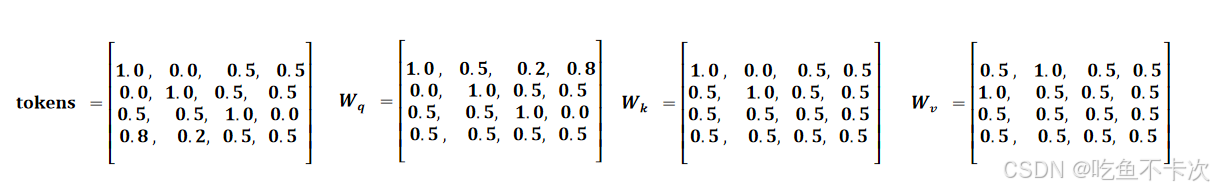
（1）首先通过矩阵乘法，可以计算得到Q、K、V的值，可以看到这一步计算得到的QKV和单头注意力计算得到的是一样的，只不过heads=2时需要将Q，K，V都拆成两组，每组的维度是2，如下所示，蓝色区域为一组，黄色区域为一组。

（2）然后计算权重，这里开始体现计算的区别了，Q1，K1和V1为一组计算，Q2，K2和V2为另一组计算，需要注意的一点是d此时是2，因为Q、K、V拆分成每个组后的列数为2，如下所示：

(3)接着分别计算输出结果为：

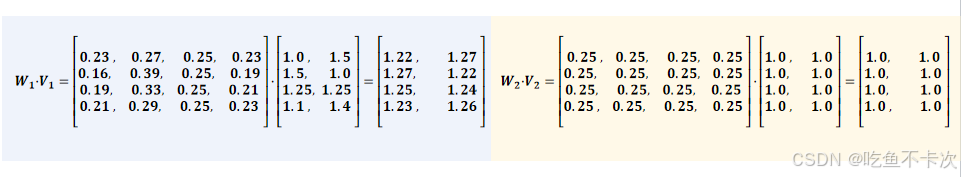
(4)最后需要对两个头的输出结果进行拼接，最后输出结果如下：

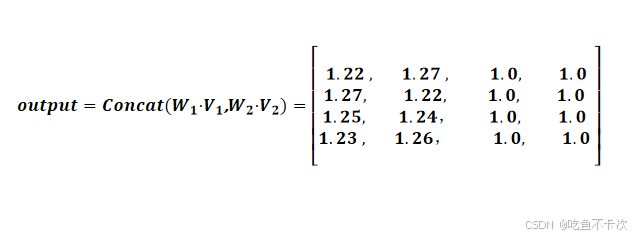
5.Vision Transformer

详细内容可以直接去看我的这篇博客，在这里我就只摘出来一部分进行介绍。

Vision Transformer网络结构-CSDN博客

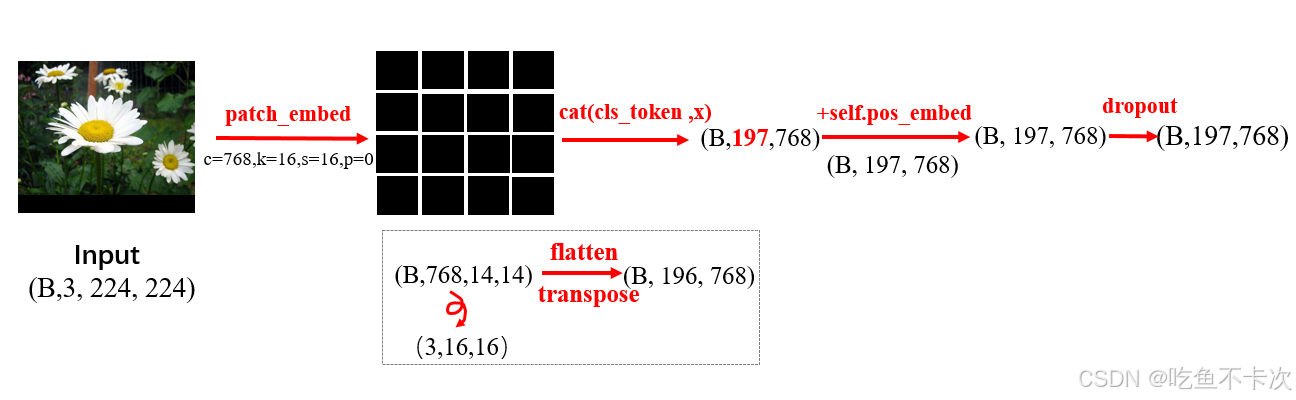
首先是图片如何转换成token，在CV中不可能对每个像素都处理成一个个token，为了降低计算量，所以设计了将图片裁剪成小块的方式，如下图所示，将一张（224,224）像素的图片按照（16,16）像素大小无重叠地切分成了196个小块，最后还需要在首位加上一个cls token，以及给每个token补充位置编码信息，将这样的输出做为tokens输入到Transformer的Encoder中。

之前我们关注的是香蕉，西瓜，电脑和耳机的相似性，在CV中我们就是去关注每个小块间的相似性，利用高维特征的相似性计算，从多个角度找到哪些小块“相似”，哪些小块“不相似”。

其次再来看下 $W_{q}, W_{k}, W_{v}$ 这三个矩阵，在CV中没有明确地去定义这样的矩阵，而是通过一个Linear层来生成三个这样的矩阵，可以理解为这三个矩阵是共享权值的，多头也是通过直接拆分Q、K、V的维度进行计算。

#Linear(in_features=768, out_features=2304, bias=True)
self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
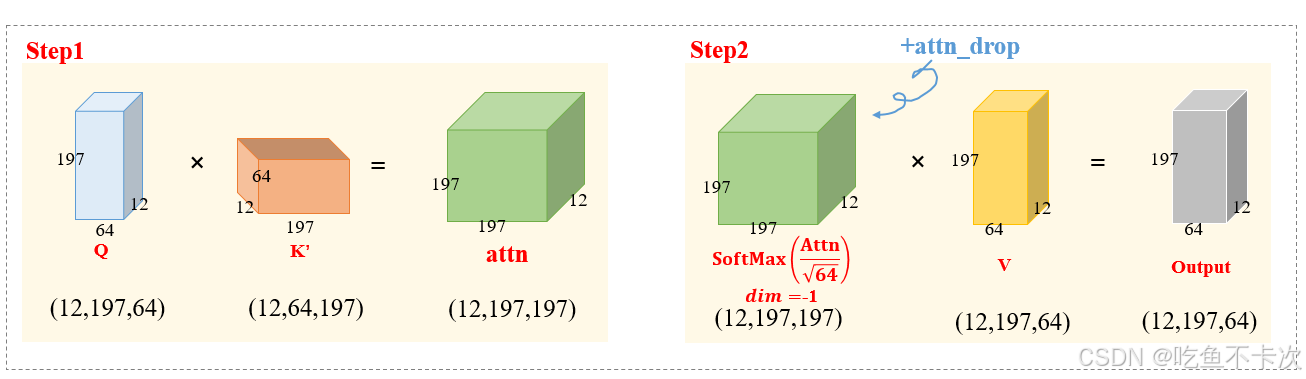
q, k, v = qkv[0], qkv[1], qkv[2]

最后看看Multi-Head Attention的核心计算过程，这部分其实就是和我们前面介绍的计算过程是一样的了。

最后再放一个DeepSeek生成的挺好的例子，假设我们有一张包含一只猫的图片，被分割成16x16的小块。

一个头可能会强烈地关注所有包含“猫毛纹理”的小块。当它处理猫肚子上的一个小块时，它会给猫背上、猫尾巴上具有相似纹理的小块分配很高的注意力权重。这样，它就在整合“猫”这个物体的整体信息。
另一个头可能会关注空间上的邻近关系。它帮助模型理解猫的鼻子小块应该和猫的眼睛、嘴巴小块关系密切，从而更好地勾勒出猫的脸部。
第三个头可能会发现一些对比性关系。例如，它可能发现“猫”的小块和背景中“沙发”的小块在特征上差异很大，从而帮助模型分离前景和背景。

参考资料：

[1]这是地表最简洁的LLM注意力讲解，吧【从零开始训练大模型03】_哔哩哔哩_bilibili

[2]注意力机制背后的数学原理：关键字、查询和值矩阵_哔哩哔哩_bilibili (没找到原作者出处，b站这个是转载的）

[3]卢菁老师.《速通深度学习数学基础》

[4]详解Transformer中Self-Attention以及Multi-Head Attention_transformer multi head-CSDN博客

posted @ 2025-10-27 20:18 yangykaifa 阅读(9) 评论(0) 收藏举报

刷新页面返回顶部