扫描线讲解,动态开点版线段树
扫描线
首先,扫描线是干什么的?扫描线一般运用在图形上面,它和它的字面意思十分相似,就是一条线在整个图上扫来扫去,它一般被用来解决图形面积,周长等问题,以一道例题为例。给出n个正方形,这些正方形在平面直角坐标系中互相重叠摆放,但四条边都与坐标轴平行,例如下图所示。那么知道题目了,怎么运用呢?首先我们需要知道怎么用暴力解决这个问题,根据图片可知图中的面积是SABCD+SHEFG-SIDJE暴力搜索是个好东西,但是当数据范围大了怎么办?这里就要讲到扫描线。

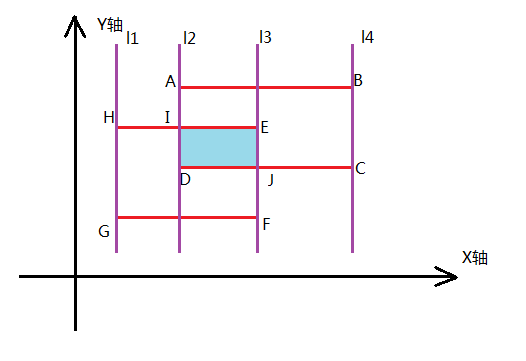
扫描线对于这道例题可以抽象为这四条紫色的直线(如上图l1,l2,l3,l4),仔细观察,可以看出这四条线把这个图形分割成三个矩形,那么我们就可以直接求这三个矩形再加和是不是就可以了?那么现在难点来了,怎样求这些矩形的面积。我们可以把题目中给的矩形的边转换成直线(如下图),即只留下这四条边,这四条线就是整个做法的核心。既然四条线已经看出来了,那么我们就可以一眼看出,面积就是从头到现在的扫描线的重影减去已经结束的长方形的边的投影承上两条扫描线的间距。再把这些乘积加在一起。

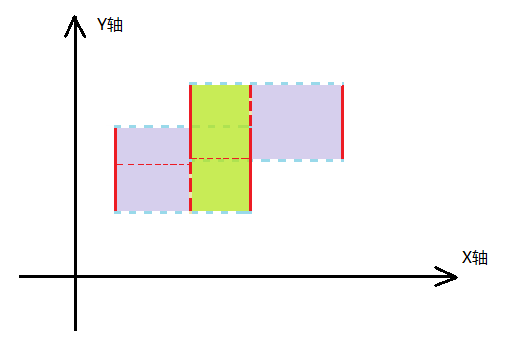
下面就将如何实现了,首先我们可以想到用线段树求区间和来求这些投影的长度,那么区间如此之大(-1e8~1e8),怎么能建树呢?不会空间爆炸吗?所以就应该运用动态开点线段树,算一下每一个扫描线开一个节点,那么就是n个,一共有log21e8层所以是可以开的下的。根据这个说法,每一条边应该进行排序,由于扫描是从左到右,所以排序应该是把横坐标从小到大排序,所以每条边有三个属性:位置即横坐标,从那个点开始,从那个点结束,这两给点分别是纵坐标的两个端点。
struct Line
{
int from,to,x,val;
}line[2001];
bool cmp1(const Line &a,const Line &b)
{
return a.x<b.x;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d%d",&a,&b,&c,&d);
line[i*2-1].x=a;
line[i*2-1].from=d+1;
line[i*2-1].to=b;
line[i*2-1].val=1;
line[i*2].x=c;
line[i*2].from=d+1;
line[i*2].to=b;
line[i*2].val=-1;
}
sort(line+1,line+1+2*n,cmp1);
}
扫描线排序
下面讲解一下如何把线段树运用进去,我们把每一条边给定一个属性,这个矩形的左面边定义为入边,给一个+1的值,右边的边定义为出边,给一个-1的值,这就是边里的val的意义,那么这个和线段树又有什么关系呢?有了这个值我们可以快速地直接给线段树赋值,让其显示是否有边覆盖在上面,也就是下面代码中的cover数组的含义,如果cover数组有值不是零,那么这个区间就有边,即有r-l+1的贡献,否则则没有。这便是查询。在查询中一定要查到叶子节点,因为在扫描线中是没有上传值或是下传值的说法。
int find(int l,int r,int p)
{
if(cover[p])
return sum[p];
if(lp==rp&&rp==0)
return 0;
int sum=0;
if(lp!=0)
sum+=find(l,(l+r)>>1,lp);
if(rp!=0)
sum+=find(((l+r)>>1)+1,r,rp);
return sum;
}
扫描线查询
最难的要数修改,如果现在的节点被现在要加的边完全覆盖,那么直接修改就好啦,否则要递归的寻找他的儿子,如果没有儿子则动态开点出来,这边是修改的想法,当然在修改时不要忘记修改cover的值。
void change(int l,int r,int x,int y,int &p,int delta)
{
if(!p)
p=++cnt;
if(x<=l&&r<=y)
{
cover[p]+=delta;
sum[p]=r-l+1;
return;
}
int mid=(l+r)>>1;
if(x<=mid)
change(l,mid,x,y,lp,delta);
if(y>mid)
change(mid+1,r,x,y,rp,delta);
}
扫描线修改
(新更)我们用这个代码,思考一道题目,就是bzoj1645城市地平线,我们可以知道TLE这个事实,但是为什么呢?由于我们每一次我们都需要查询,每一次查询都是至少O(n)以上的时间复杂度,这样我们整体的时间复杂度就是大于O(n^2),我们需要优化一下,我们可以开一个叫做sum的数组,也就是我们把上面的sum数组重新定义一下就可以了,在这里我们定义sum数组为当前区间之中所有的边的和,那么我们很容易知道,如果当前的区间的cover值大于零,sum数组就位当前区间的r-l+1,如果cover等于零,sum数组的值就等于他的左右儿子的sum数组的值相加,是不是很简单?根据定义整个图形中的线段和就位跟的sum值。下面是更改后的区间修改以及pushup函数,当然由于我们可以O(1)求出整个图形之中的线段和,所以find函数就没有了。
void pushup(int p,int l,int r)
{
if(cover[p]>0) sum[p]=r-l+1;
else sum[p]=sum[lson[p]]+sum[rson[p]];
}
void change(int l,int r,int x,int y,int &p,int delta)
{
if(!p) p=++cnt;
if(x<=l&&r<=y)
{
cover[p]+=delta;
pushup(p,l,r);
return;
}
int mid=(l+r)>>1;
if(x<=mid) change(l,mid,x,y,lson[p],delta);
if(y>mid) change(mid+1,r,x,y,rson[p],delta);
pushup(p,l,r);
}
大致就是这样,不会的可以评论发问题,我会解答。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号