矩阵树定理浅谈
矩阵树定理浅谈
一、前置知识
在学习矩阵树定理之前,要知道什么是生成树,知道怎么运用高斯消元求一个矩阵的行列式。
二、定理内容
这个定理共分为三个部分:1.给出无向图,求这个图的生成树个数。2.给出有向图和其中的一个点,求以这个点为根的生成外向树个数。3.给出有向图和其中一个点,求以这个点为根的生成内向树个数。
部分一:我们对这个图构造两个矩阵,分别是这个图的连通矩阵和度数矩阵。连通矩阵$S_1$的第$i$行第$j$列上的数字表示原无向图中编号为$i$和编号为$j$的两个点之间的边的条数。度数矩阵$S_2$只有斜对角线上有数字,即只有第$i$行第$i$列上有数字,表示编号为$i$的点的度数是多少。我们将两个矩阵相减,即$S_2-S_1$,我们记得到的矩阵为$T$,我们将矩阵$T$去掉任意一行和一列(一般情况去掉最后一行和最后一列的写法比较多)得到$T'$,最后生成树的个数就是这个矩阵$T' $的行列式。
部分二:我们对这个图构造两个矩阵,分别是这个图的连通矩阵和度数矩阵。连通矩阵$S_1$的第$i$行第$j$列上的数字表示原无向图中编号为$i$和编号为$j$的两个点之间编号$i$的点指向编号为$j$的点的条数。度数矩阵$S_2$只有斜对角线上有数字,即只有第$i$行第$i$列上有数字,表示编号为$i$的点的入度是多少。我们将两个矩阵相减,即$S_2-S_1$,我们记得到的矩阵为$T$,我们将矩阵$T$去掉根所在行和根所在列得到$T'$,最后生成树的个数就是这个矩阵$T' $的行列式。
部分三:我们对这个图构造两个矩阵,分别是这个图的连通矩阵和度数矩阵。连通矩阵$S_1$的第$i$行第$j$列上的数字表示原无向图中编号为$i$和编号为$j$的两个点之间编号$i$的点指向编号为$j$的点的条数。度数矩阵$S_2$只有斜对角线上有数字,即只有第$i$行第$i$列上有数字,表示编号为$i$的点的出度是多少。我们将两个矩阵相减,即$S_2-S_1$,我们记得到的矩阵为$T$,我们将矩阵$T$去掉根所在行和根所在列得到$T'$,最后生成树的个数就是这个矩阵$T' $的行列式。
三、例题
题目描述:你突然有了一个大房子,房子里面有一些房间。事实上,你的房子可以看做是一个包含n*m个格子的格状矩形,每个格子是一个房间或者是一个柱子。在一开始的时候,相邻的格子之间都有墙隔着。
你想要打通一些相邻房间的墙,使得所有房间能够互相到达。在此过程中,你不能把房子给打穿,或者打通柱子(以及柱子旁边的墙)。同时,你不希望在房子中有小偷的时候会很难抓,所以你希望任意两个房间之间都只有一条通路。现在,你希望统计一共有多少种可行的方案。
题目讲解:这是一道十分简单的矩阵树定理的题目,我们将每一个房子看做一个节点,对于隔开两个房子的一堵墙看做连接两个点的一条无向边,这样就是无向图求生成树个数。
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
#define N 20
#define eps 1e-10
#define mod 1000000000
int n,m,num[N][N],cnt;
int dicx[5]={0,0,0,1,-1},dicy[5]={0,1,-1,0,0};
bool map[N][N];char str[N];
long long ans=1,square[N*N][N*N];
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%s",str+1);
for(int j=1;j<=m;j++) map[i][j]=(str[j]=='.');
}
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
if(map[i][j]) num[i][j]=++cnt;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int k=1;k<=4;k++)
if(map[i+dicx[k]][j+dicy[k]]&&map[i][j])
{
square[num[i][j]][num[i][j]]++,
square[num[i][j]][num[i+dicx[k]][j+dicy[k]]]--;
}
for(int i=1;i<cnt;i++)
{
int j;
for(j=i;j<cnt;j++)
if(square[j][i]) break;
if(j==cnt) continue;
if(j!=i)
{
for(int k=i;k<cnt;k++)
swap(square[i][k],square[j][k]);
ans*=-1;
}
for(j=i+1;j<cnt;j++)
{
while(square[j][i])
{
int t=square[j][i]/square[i][i];
for(int k=i;k<cnt;k++)
square[j][k]=(square[j][k]-square[i][k]*t%mod+mod)%mod;
if(!square[j][i]) break;
for(int k=i;k<cnt;k++)
swap(square[i][k],square[j][k]);
ans*=-1;
}
}
}
for(int i=1;i<cnt;i++)
ans*=square[i][i],ans%=mod;
printf("%lld\n",(ans%mod+mod)%mod);
}
例二:bzoj1002轮状病毒
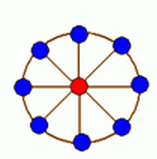
题目描述:轮状病毒有很多变种。许多轮状病毒都是由一个轮状基产生。一个n轮状基由圆环上n个不同的基原子和圆心的一个核原子构成。2个原子之间的边表示这2个原子之间的信息通道,如图1。
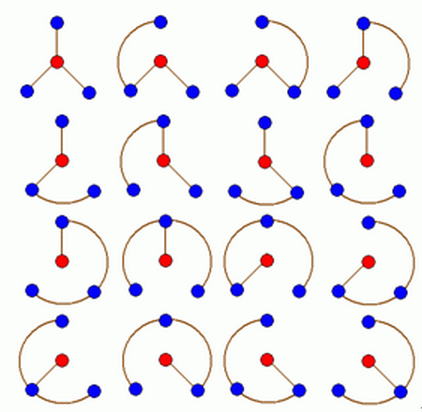
n轮状病毒的产生规律是在n轮状基中删除若干边,使各原子之间有唯一一条信息通道。例如,共有16个不同的3轮状病毒,入图2所示。
给定n(N<=100),编程计算有多少个不同的n轮状病毒。
题目讲解:我们发现这是一道无向图的生成树计数问题,我们考虑一个$n$轮状基得到的行列式是(下图所示)。

对于上方的行列式一共有$n$行$n$列,我们通过找规律(推式子)可以发现,这个行列式可以递推,我们设$f[i]$表示$i$轮状基的行列式值,则$f[i]=3\times f[i-1]-f[i-2]+2$。最后用高精度算一下就好了。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define mod 100000000
#define N 1000
int n;
struct Num
{
long long num[N];
Num() {memset(num,0,sizeof(num));}
void print()
{
for(int i=num[0];i;i--)
(i==num[0])?printf("%lld",num[i]):printf("%08lld",num[i]);
printf("\n");
}
Num operator + (const Num &a) const
{
Num ans;ans.num[0]=max(a.num[0],num[0]);long long tmp=0;
for(int i=1;i<=ans.num[0];i++)
ans.num[i]=num[i]+a.num[i]+tmp,tmp=ans.num[i]/mod,ans.num[i]%=mod;
while(tmp) ans.num[++ans.num[0]]=tmp%mod,tmp/=mod;
return ans;
}
Num operator - (const Num &a) const
{
Num ans;ans.num[0]=num[0];long long tmp=0;
for(int i=1;i<=ans.num[0];i++)
{
if(num[i]-tmp-a.num[i]<0) ans.num[i]=num[i]-tmp-a.num[i]+mod,tmp=1;
else ans.num[i]=num[i]-tmp-a.num[i],tmp=0;
}
while(ans.num[ans.num[0]]==0) ans.num[0]--;
return ans;
}
Num operator * (const Num &a) const
{
Num ans,tmp;long long tmp1=0,tmp2;
for(int i=1;i<=a.num[0];i++)
{
tmp2=a.num[i],tmp.num[0]=i-1,tmp1=0,tmp.num[tmp.num[0]]=0;
for(int j=1;j<=num[0];j++)
{
tmp.num[++tmp.num[0]]=num[j]*tmp2+tmp1;
tmp1=tmp.num[tmp.num[0]]/mod,tmp.num[tmp.num[0]]%=mod;
}
while(tmp1) tmp.num[++tmp.num[0]]=tmp1%mod,tmp1/=mod;
ans=ans+tmp;
}return ans;
}
Num operator ^ (const int &a) const
{
Num ans,x;int y=a;ans.num[0]=ans.num[1]=1;
for(int i=0;i<=num[0];i++) x.num[i]=num[i];
while(y) {if(y&1) ans=ans*x;x=x*x,y>>=1;} return ans;
}
}ans[200],tmp,tmp1;
void solve()
{
tmp.num[1]=3,tmp1.num[1]=2,tmp1.num[0]=tmp.num[0]=ans[1].num[0]=ans[1].num[1]=1;
for(int i=2;i<=n;i++) ans[i]=ans[i-1]*tmp-ans[i-2]+tmp1;
}
int main() {scanf("%d",&n),solve(),ans[n].print();}
例三:bzoj2467生成树
题目描述:有一种图形叫做五角形圈。一个五角形圈的中心有1个由n个顶点和n条边组成的圈。在中心的这个n边圈的每一条边同时也是某一个五角形的一条边,一共有n个不同的五角形。这些五角形只在五角形圈的中心的圈上有公共的顶点。如图0所示是一个4-五角形圈。

现在给定一个n五角形圈,你的任务就是求出n五角形圈的不同生成树的数目。还记得什么是图的生成树吗?一个图的生成树是保留原图的所有顶点以及顶点的数目减去一这么多条边,从而生成的一棵树。
注意:在给定的n五角形圈中所有顶点均视为不同的顶点。
题目讲解:这显然是一道优秀的矩阵树定理裸题,值得注意的是这道题目当$n==2$时需要特判。这还有一种组合数的做法,本人写的是组合数的方法。
例四:bzoj4894天赋
题目描述:小明有许多潜在的天赋,他希望学习这些天赋来变得更强。正如许多游戏中一样,小明也有n种潜在的天赋,但有一些天赋必须是要有前置天赋才能够学习得到的。也就是说,有一些天赋必须是要在学习了另一个天赋的条件下才能学习的。比如,要想学会"开炮",必须先学会"开枪"。一项天赋可能有多个前置天赋,但只需习得其中一个就可以学习这一项天赋。上帝不想为难小明,于是小明天生就已经习得了1号天赋-----"打架"。于是小明想知道学习完这n种天赋的方案数,答案对1,000,000,007取模。
题目讲解:我们看这道题目,显然是一道有向图,题目中要我们求的就是以$1$为根的外向生成树个数,这个就是我们在第二大点中讲述的第二部分。
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
#define N 300
#define eps 1e-10
#define mod 1000000007
int n;long long ans=1,square[N][N];
int main()
{
scanf("%d",&n),n--;
for(int i=0;i<=n;i++) for(int j=0,a;j<=n;j++)
{
scanf("%1d",&a);
if(a==1) square[j][j]++,square[i][j]--;
}
for(int i=1;i<=n;i++)
{
int j;for(j=i;j<=n;j++) if(square[j][i]) break;
if(j==n+1) continue;
if(j!=i)
{
for(int k=i;k<=n;k++)
swap(square[i][k],square[j][k]);
ans*=-1;
}
for(j=i+1;j<=n;j++)
{
while(square[j][i])
{
int t=square[j][i]/square[i][i];
for(int k=i;k<=n;k++)
square[j][k]=(square[j][k]-square[i][k]*t%mod+mod)%mod;
if(!square[j][i]) break;
for(int k=i;k<=n;k++)
swap(square[i][k],square[j][k]);
ans*=-1;
}
}
}
for(int i=1;i<=n;i++) ans*=square[i][i],ans%=mod;
printf("%lld\n",(ans%mod+mod)%mod);
}
例五:bzoj5056OI游戏
题目描述:小Van的CP最喜欢玩与OI有关的游戏啦~小Van为了讨好她,于是冥思苦想,终于创造了一个新游戏。下面是小Van的OI游戏规则:给定一个无向连通图,有N个节点,编号为0~N-1。图里的每一条边都有一个正整数权值,边权在1~9之间。要求从图里删掉某些边(有可能0条),使得剩下的图满足以下两个条件:
1) 剩下的图是一棵树,有N-1条边。
2) 对于所有v (0 < v < N),0到v的最短路(也就是树中唯一路径长度)和原图中的最短路长度相同。
最终要报出有多少种不同的删法可以满足上述条件。(两种删法不同当且仅当存在两个点,一种删法删完之后这两个点之间存在边而另外一种删法不存在。)由于答案有可能非常大,良心的小Van只需要答案膜1,000,000,007的结果。
题目讲解:我们可以先求出任意两个点的最短路,这样我们就可以判断那些边可以留。我们现在假设第$i$条边连接了$x$,$y$两个点,这两个点到点$0$的最短路分别为$dis_x$和$dis_y$,若$dis_x+val_i==dis_y$,则$y$的最短路可以由$x$转移过来,这样我们保留一条从$x$指向$y$的有向边,这样题目就转化成为$0$为根的外向生成树的个数。
#include <cstdio>
#include <algorithm>
using namespace std;
#define inf 1000000000
#define mod 1000000007
#define N 51
int n,dis[N][N],dis2[N][N];long long ans=1,squ[N][N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
{
scanf("%1d",&dis[i][j]),dis2[i][j]=dis[i][j];
if(i!=j&&(!dis[i][j])) dis[i][j]=inf;
}
for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
if(dis2[i][j]&&dis[1][i]+dis2[i][j]!=dis[1][j]) dis2[i][j]=0;
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
if(dis2[i][j]) squ[j-1][j-1]++,squ[i-1][j-1]--; n--;
for(int i=1;i<=n;i++)
{
int j;for(j=i;j<=n;j++) if(squ[j][i]) break;
if(j==n+1) continue;
if(i!=j) {for(int k=i;k<=n;k++) swap(squ[i][k],squ[j][k]);ans*=-1;}
for(j=i+1;j<=n;j++)
{
while(squ[j][i])
{
int t=squ[j][i]/squ[i][i];
for(int k=i;k<=n;k++)
squ[j][k]=(squ[j][k]-squ[i][k]*t%mod+mod)%mod;
if(!squ[j][i]) break;
for(int k=i;k<=n;k++)
swap(squ[i][k],squ[j][k]);
ans*=-1;
}
}
}
for(int i=1;i<=n;i++) (ans*=squ[i][i])%=mod;
printf("%lld\n",(ans%mod+mod)%mod);
}
题目描述:四年一度的幻想乡大选开始了,最近幻想乡最大的问题是很多来历不明的妖怪涌入了幻想乡,扰乱了幻想乡昔日的秩序。但是幻想乡的建制派妖怪(人类)博丽灵梦和八云紫等人整日高谈所有妖怪平等,幻想乡多元化等等,对于幻想乡目前面临的种种大问题却给不出合适的解决方案。风间幽香是幻想乡里少有的意识到了问题的严重性的大妖怪。她这次勇敢的站了出来参加幻想乡大选。提出包括在幻想乡边境建墙(并让人类出钱),大力开展基础设施建设挽回失业率等一系列方案,成为了大选年出人意料的黑马并顺利的当上了幻想乡的大统领。
幽香上台以后,第一项措施就是要修建幻想乡的公路。幻想乡有 N 个城市,之间原来没有任何路。幽香向选民承诺要减税,所以她打算只修 N- 1 条路将这些城市连接起来。但是幻想乡有正好 N- 1 个建筑公司,每个建筑公司都想在修路的过程中获得一些好处。虽然这些建筑公司在选举前没有给幽香钱,幽香还是打算和他们搞好关系,因为她还指望他们帮她建墙。所以她打算让每个建筑公司都负责一条路来修。每个建筑公司都告诉了幽香自己有能力负责修建的路是哪些城市之间的。所以幽香打算选择 N-1 条能够连接幻想乡所有城市的边,然后每条边都交给一个能够负责该边的建筑公司修建,并且每个建筑公司都恰好修一条边。幽香现在想要知道一共有多少种可能的方案呢?两个方案不同当且仅当它们要么修的边的集合不同,要么边的分配方式不同。
题目讲解:我们看$n$十分小,我们可以考虑容斥原理,我们容斥一下,每一次都用矩阵树定理来做,我们设$calc(i)$为假设钦定$i$个建筑公司不选,其他的随意的方案数,最后的答案即为:$ans=calc(0)-calc(1)+calc(2)-……$。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define mod 1000000007
#define N 70
int n,many[N],from[N][N],to[N][N];long long ans,squ[N][N];
long long calc()
{
long long tmp=1;
for(int i=1;i<n;i++)
{
int j;for(j=i;j<n;j++) if(squ[j][i]) break;
if(j==n) continue;
if(j!=i) {for(int k=i;k<n;k++) swap(squ[i][k],squ[j][k]);tmp*=-1;}
for(j=i+1;j<n;j++)
{
while(squ[j][i])
{
long long t=squ[j][i]/squ[i][i];
for(int k=i;k<n;k++)
squ[j][k]=(squ[j][k]-squ[i][k]*t%mod+mod)%mod;
if(!squ[j][i]) break;
for(int k=i;k<n;k++)
swap(squ[i][k],squ[j][k]);
tmp*=-1;
}
}
}
for(int i=1;i<n;i++) (tmp*=squ[i][i])%=mod; return tmp;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<n;i++) {scanf("%d",&many[i]);
for(int j=1;j<=many[i];j++) scanf("%d%d",&from[i][j],&to[i][j]);}
for(int i=0;i<(1<<(n-1));i++)
{
int times=n-1;memset(squ,0,sizeof squ);
for(int j=1;j<n;j++) if(i>>(j-1)&1) times--;
for(int j=1;j<n;j++) if(i>>(j-1)&1)
for(int k=1;k<=many[j];k++)
squ[from[j][k]][from[j][k]]++,squ[to[j][k]][to[j][k]]++,
squ[from[j][k]][to[j][k]]--,squ[to[j][k]][from[j][k]]--;
long long tmp=calc();if(times&1) tmp*=-1; (ans+=tmp)%=mod;
} printf("%lld\n",(ans%mod+mod)%mod);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号