Pytorch 3.4.3 Softmax 负对数似然

负对数似然

当你看不懂的时候就请放下你的浮躁和各种想法，静下来好好琢磨琢磨这一件事情。

我们先来温习下最大似然函数 (Maximum Likelihood Estimation, MLE)

《茆诗松概率论与数理统计》第六章 例：6.3.1

设有外形完全相同的两个箱子，甲箱中有99个白球和1个黑球，乙箱中99个黑球和1个白球，今随机地抽取一箱，并从中随机抽取一球，结果取得白球，问这球是从哪一个箱子中取出？

解: 不管是哪一个箱子，从箱子中任取一球都有两个可能的结果：

\(A\) 表示“取出白建＂, \(B\) 表示“取出黑球”．

如果我们取出的是甲箱，则 \(A\)发生的概率为0.99，而如果取出的是乙箱，则 \(A\) 发生的概率为\(0.01\)．

现在一次试验中结果 \(A\) 发生了，人们的第一印象就是．“此白球 \(A\) 最像从甲箱取出的”，或者说，应该认为试验条件对结果 A 出现有利，从而可以推断这球是从甲箱中取出的．这个推断很符合人们的经验事实，这里“最像”就是“最大似然”之意．这种想法常称为“最大似然原理”.

本例中假设的数据很极端．一般地，我们可以这样设想：有两个箱子中各有100只球，甲箱中白球的比例是 P ，乙箱中白球的比例是 P ，已知 P > P ，现随机地抽取一个箱子并从中抽取一球，假定取到的是白球，如果我们要在两个箱子中进行选择，由于甲箱中白球的比例高于乙箱，根据最大似然原理，我们应该推断该球来自甲箱．

例6.3.2 假设产品分为合格和不及格两个类别， 用随机变量\(X\) 表示某个产品经检查之后的不及格数量，则\(X = 0\) 表示及格产品，\(X = 1\) 表示不及格的产品，则\(X\)服从两点分布 \(b(1,p)\) ，其中的 \(p\) 是不及格率 ，现在抽取 \(n\) 个产品看其是否及格，得到样本 \(x_1,x_2, \cdots ,x_n\) 这批观测值发生的概率为：

\[P(X_1 = x_1,X_2 = x_2, \cdots , X_n = x_n;p) = \prod_{i=1}^{n} p^{x_i} (1-p)^{1-x_i} = p^{\sum_{i=1}^{n} x_i} (1-p)^{n-\sum_{i=1}^{n} x_i} \tag{6.3.1} \]

由于\(p\) 是未知的，根据最大似然原理，我们应该选择\(p\) 使得\(（6.3.1）\)表示的概率尽可能大，将\((6.3.1)\) 看做未知参数\(p\)的函数，用\(L(p)\) 来表示，称作为似然函数 ：

\[L(p) = p^{\sum_{i=1}^{n} x_i} (1-p)^{n-\sum_{i=1}^{n} x_i} \tag{6.3.2} \]

要求\((6.3.2)\) 的最大值点不是难事，将\((6.3.2)\) 两端取对数并关于\(p\) 求导令其为零，得到的方程称为似然方程：

\[\frac{\partial \ln L(p)}{\partial p} = \frac{\sum_{x=1}^{n} x_i}{p} - \frac{n - \sum_{i=1}^{n} x_i}{1-p} = 0 \]

求解得到\(p\) 的最大似然估计： (不知道如何求解的自己推到一遍)

\[\hat{p} = \hat{p}(x_1,x_2,x_3,\cdots,x_n) = \frac{1}{n}\sum_{i=1}^{n} x_i = \bar{x} \]

\(L(\hat{p}) = \max L(p)\) 就是我们要的参数。 故我么称之为 最大似然函数 ，简记为MLE( Maximum likelihood estimate) .

最大似然估计的一般步骤如下:
(1) 写出似然函数;
(2) 对似然函数取对数,得到对数似然函数;
(3) 求对数似然函数的关于参数组的偏导数,并令其为0,得到似然方程组;
(4) 解似然方程组,得到参数组的值。

(1) \(e.g: L(\theta) = p^{\sum_{i=1}^{n} x_i} (1-p)^{n-\sum_{i=1}^{n} x_i}\)
(2) \(\log L(\theta)\)
(3) \(\frac{\partial \log L(p)}{\partial p} = 0\)
(4) \(\hat{\theta} = \arg\max _\theta L(\theta)\)

负对数似然(Negative log-likelihood, NLL)

那么有同学要问了，什么交叉熵，什么相对熵，什么对数似然函数，现在又来一个负对数似然函数，杨大大，你搞得我头都大了，能不能讲的通俗点？ -- 安排

对数似然函数就是我们上面所说的，所谓负对数似然函数就是单纯的在前面添加一个负号 \(l(θ) = -\log L(θ) = -\log P_G(x_i;θ)\) ，其中的\(P_G(x_i;θ)\) 指的是我们定义的一个分布模型，就好像是上面例6.3.2所说的二项分布\(b(1,p)\) 该分布由参数\(\theta\) 决定。

为什么要取多一个负号？其实这并不是脱裤子放屁，由于对数似然函数是对概率求对数，\(P(x)∈[0,1]\) 取对数之后：\(\log P(x) ∈ (-\infty , 0]\) ,如果我们在前面添加一个负号的话，\(-\log P(x) ∈[0,+\infty)\)

\[l(\theta) = -\sum_{i=1}^{m}\log(P_G(x_i;\theta)) \]

这个公式正好是我们的交叉熵损失函数，只是前面少了一项 \(p(x_i)\) ,但是我们真是标签的预测值就是0或者1呀，所以省略掉了。

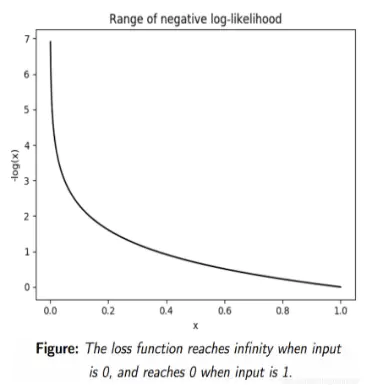
我们期望似然估计越大越好，取完负号之后就是负对数似然越小越好，因此负对数似然函数可以作为损失函数。

Pytorch 实现

Pytorch中对应的负对数似然损失函数为：

torch.nn.NLLLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

值得注意的是，在使用该损失函数的时候并不需要将标签转换成one-hot形式，c类标签，就用c-1个数表示即可。
input: (N,C)output:(N)其中的N是batch_size大小，C是分类的数量

import torch 
import torch.nn as nn 

m = nn.LogSoftmax(dim=1)
loss = nn.NLLLoss() 
features = torch.tensor([[-0.3280, -0.6004, -0.1753,  1.2293,  1.5320],
        [-0.4770, -2.7324,  0.5937, -1.8657,  0.4829],
        [-1.5907,  0.9821, -1.3793,  0.7273,  0.0256]], requires_grad=True) # 三行五列，三个样本一共五个类别 
labels = torch.tensor([1,0,3]) #第一个样本是二号，第二个样本是一号，第三个样本是四号 
output = loss(m(features),labels) 
output ,m(features)

out[0]:
    (tensor(1.9827, grad_fn=<NllLossBackward0>),
 tensor([[-2.6459, -2.9183, -2.4932, -1.0886, -0.7859],
         [-1.9291, -4.1845, -0.8584, -3.3178, -0.9692],
         [-3.4186, -0.8458, -3.2072, -1.1006, -1.8023]],
        grad_fn=<LogSoftmaxBackward0>))

计算结果分析：

m(features):
tensor([[-2.6459, -2.9183, -2.4932, -1.0886, -0.7859],
         [-1.9291, -4.1845, -0.8584, -3.3178, -0.9692],
         [-3.4186, -0.8458, -3.2072, -1.1006, -1.8023]],
        grad_fn=<LogSoftmaxBackward0>))

选出数据：-2.9183 ，-1.9291 ，-1.1006 --->算下：(-2.9183-1.9291-1.1006)/3 = -1.9826666666666668

我们再来使用下torch.nn.CrossEntropyLoss()验证下我们的猜想：这个公式正好是我们的交叉熵损失函数，只是前面少了一项 \(p(x_i)\) ,但是我们真是标签的预测值就是0或者1呀，所以省略掉了。

CrossEntropyLoss = nn.CrossEntropyLoss()
CrossEntropyLoss(features,labels)

out[1]: 
    tensor(1.9827, grad_fn=<NllLossBackward0>)

结果完全符合预期。赞！

值得注意的是，nn.NLLLoss()函数虽然叫负对数似然损失函数，但是该函数内部并没有像公式里那样进行了对数计算，而是在激活函数上使用了nn.LogSoftmax()函数，所以nn.NLLLoss()函数只是做了求和取平均然后再取反的计算，在使用时要配合logsoftmax函数一起使用，或者直接使用交叉熵损失函数。

参考文章/文献：
《茆诗松概率论与数理统计第三版》(可自行下载查看)
[损失函数]——负对数似然 简书：一位学有余力的同学