Pytorch 3.2 线性回归简单实现

线性回归简单实现

由于正规方程在实际应用中十分受限，所以我们一致采用最普遍的优化方式：小批量梯度下降
梯度下降原理：
小批量梯度下降：


对于小批量梯度下降，我们需要通过我们CPU和GPU的性能选择批量\(b\)大小，学习率lr的选择等，但是在目前的话，我们还无需理会过多。

我们使用一下的模型进行学习： $$\mathbf{y}= \mathbf{X} \mathbf{w} + b + \mathbf\epsilon.$$
\(\mathbf\epsilon\)指的是噪声，\(\mathbf{X}\)指的是输入的样本 ，\(\mathbf{w}\)权重
我们可以将 \(𝜖\) 视为捕获特征和标签时的潜在观测误差。在这里我们认为标准假设成立，即 \(𝜖\) 服从均值为0的正态分布。 为了简化问题，我们将标准差设为0.01。下面的代码生成合成数据集

生成数据

def synthetic_data(w,b,num_examples): # 生成数据 parameters: w ,b ,num_examples 样本数量  
    '''生成 y = Xw +b + 噪声的数据'''
    X = torch.normal(mean=0,std=1,size=(num_examples,len(w)))  #生成mean=0,std=1，大小为size 的N(0,1)样本
    y = torch.matmul(X,w)+b # matmul(A,B):AB张量相乘，当A,B均为二维的时候，可以理解成矩阵相乘
    y += torch.normal(mean=0,std=0.01,size=(y.shape))  # 添加噪音
    return X,y.reshape((-1,1))

不懂torch.normal()和torch.matul()用法的建议去补补。

true_w = torch.arange(1.,3.)
true_b = 5.5 
features,labels = synthetic_data(true_w,true_b,1000) # fea..[1000,2] lab..[1000,1]
print(features[0],labels[0]) 

输出:tensor([ 0.5419, -0.2366]) tensor([5.5746]) \((0.54*1-0.23*2)+5.5 ≈ 5.5746\) 说明生成的数据是大致正确的✔

绘制生成数据的散点图

除了生成数据还不行，我们还得知道数据的关系，比如线性关系等。

plt.scatter(features[:,1].detach().numpy(),labels.detach().numpy(),1) # w[1] = 3 斜率接近3的线性关系 
plt.show() 

输出：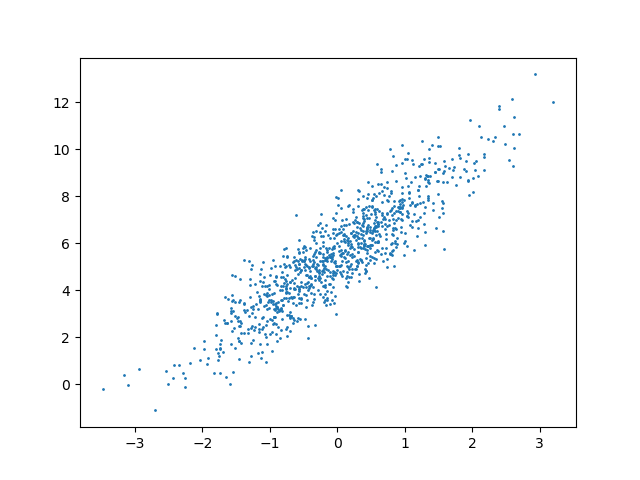
通过观察，我们传入的参数w[1]是3，也就是说，在 样本的第二个特征生成的散点图大致符合这一斜率。说明生成的数据无误 ✔

读取数据

以上生成的数据符合某种线性关系，但是我们一般接受到真实的数据都是陌生的，因此，为了还原真实性，我们需要打乱数据，random.shuffle()

# 定义一个data_iter函数， 该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量
def data_iter(batch_size,features,labels):
    num_examples = len(features) # feature[:,:] 逗号前面是样本的数量 ，len(features)返回的是dim=0的数据
    indices = list(range(num_examples))  # 得到数据的index 
    random.shuffle(indices)  # 洗牌
    
    for i in range(0,num_examples,batch_size): #  ｛----｝：bench_size i+=｛----｝、｛----｝、｛----｝、 ... 、{i,num_examples-i} 
        batch_indices = torch.tensor(
            indices[i:min(i+batch_size,num_examples)])
        yield features[batch_indices],labels[batch_indices]   

好了，好了，我们来直观理解下，看下数据本身：(说实话，其实人是看不出来的，...因为每次运行都会刷新，除非定义随机数种子)

# 直观理解下 
batch_size = 10 
for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

输出：

tensor([[-0.6124, -0.9695],
        [ 1.3726,  1.8001],
        [ 0.1235,  0.5941],
        [ 0.6265, -1.0635],
        [-1.3062,  1.3881],
        [ 1.5498,  2.9676],
        [ 0.3512, -1.5761],
        [ 0.5938,  0.9582],
        [ 0.5334, -0.2781],
        [ 1.1478, -0.9901]]) 
 tensor([[ 2.9413],
        [10.4602],
        [ 6.8080],
        [ 4.0030],
        [ 6.9563],
        [12.9923],
        [ 2.7082],
        [ 7.9977],
        [ 5.4776],
        [ 4.6634]])
''' 

定义函数和模型

#定义模型 
def LinerRegression(X,w,b):
    return torch.matmul(X,w)+b 

#定义损失函数
def squared_loss(y_hat,y): 
    return (y_hat -y.reshape(y_hat.shape))**2/2

#定义优化算法 
def sgd(params, lr ,batch_size): 
    '''small batch gradient decent'''
    with torch.no_grad():
        for param in params:
            param -= lr*param.gard / batch_size 
            param.gard.zero_()

训练数据

# 初始化模型参数 
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
lr = 0.03 # learning Rate 
num_epochs = 3 # 迭代周期（epoch）
net = linreg # Model type 
loss = squared_loss # loss function 

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # `X`和`y`的小批量损失
        # 因为`l`形状是(`batch_size`, 1)，而不是一个标量。`l`中的所有元素被加到一起，
        # 并以此计算关于[`w`, `b`]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

输出：

epoch 1, loss 0.043538
epoch 2, loss 0.000165
epoch 3, loss 0.000050

整个文章的所有代码整合

下面是本文章中一些零碎的知识点，如果果你还想看的话。

normal(mean, std, *, generator=None, out=None)

该函数返回从单独的正态分布中提取的随机数的张量，该正态分布的均值是mean，标准差是std ,这个函数有哦两种形式 给定mean和std生成一个大小为size的矩阵
或者直接给定 张量的mean和张量的std，直接生成一个张量

torch.matmul是tensor的乘法，输入可以是高维的。 当输入是都是二维时，就是普通的矩阵乘法，和tensor.mm函数用法相同。

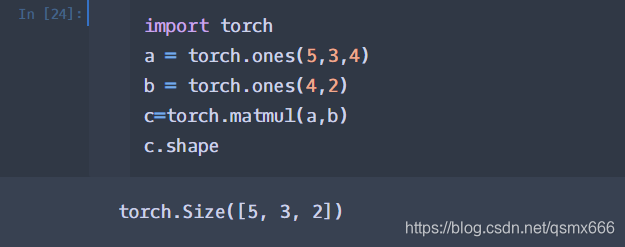
with torch.no_grad():

1.关于with:
with是python中上下文管理器，简单理解，当要进行固定的进入，返回操作时，可以将对应需要的操作，放在with所需要的语句中。比如文件的写入（需要打开关闭文件）等
以下为一个文件写入使用with的例子。

with open (filename,'w') as sh:    
    sh.write("#!/bin/bash\n")
    sh.write("#$ -N "+'IC'+altas+str(patientNumber)+altas+'\n')
    sh.write("#$ -o "+pathSh+altas+'log.log\n') 
    sh.write("#$ -e "+pathSh+altas+'err.log\n') 
    sh.write('source ~/.bashrc\n')          
    sh.write('. "/home/kjsun/anaconda3/etc/profile.d/conda.sh"\n')
    sh.write('conda activate python27\n')
    sh.write('echo "to python"\n')
    sh.write('echo "finish"\n')
    sh.close()

with后部分，可以将with后的语句运行，将其返回结果给到as后的变量（sh），之后的代码块对close进行操作。
2.关于with torch.no_grad():

# 被with torch.no_grad()包住的代码，不用跟踪反向梯度计算，来做一个实验：
a = torch.tensor([1.1], requires_grad=True)
b = a * 2
b # tensor([2.2000], grad_fn=<MulBackward0>)
b.add_(2) # tensor([4.2000], grad_fn=<AddBackward0>) 表明是add的反向梯度函数
with torch.no_grad():
    b.mul_(2) # 输出b： tensor([8.4000], grad_fn=<AddBackward0>)
# 可以看到没有跟踪乘法的梯度，还是上面的加法的梯度函数，不过乘法是执行了的

在使用pytorch时，并不是所有的操作都需要进行计算图的生成（计算过程的构建，以便梯度反向传播等操作）。而对于tensor的计算操作，默认是要进行计算图的构建的，在这种情况下，可以使用 with torch.no_grad():，强制之后的内容不进行计算图构建。