不同复杂度记号的说明

1. Big-O: \(O().\)

这个很常用, 给出了算法的复杂度上界.

\(f(n) \in O(g(n)): \exists c > 0, \exists n_0\) such that \(\forall n \geq n_0, f(n) \leq cg(n).\)

2. Little-o: \(o().\)

\(f(n) \in o(g(n)): \forall c > 0, \exists n_0\) such that \(\forall n \geq n_0, f(n) < cg(n).\)

一般来说, 大O表示了一个比较紧致的上界, 小o表示了一个不那么紧致的上界.

3. Big-Omega: $\Omega(). $

用来表示算法的渐进意义的下界, 分析的是算法的最好情况下(best case)的开销.

$ f(n) = \Omega(g(n)): \exists c > 0, \exists n_0$ such that \(\forall n \geq n_0, f(n) \geq cg(n).\)

在算法分析中, 这个符号使用的比较少, 因为这个记号给出的是正确但不精确的界(比如1M和10都大于1).

4. Little-omega: \(\omega().\)

\(f(n) \in \omega(g(n)): \forall c > 0, \exists n_0\) such that \(\forall n \geq n_0, f(n) > cg(n).\)

同样, 大Omega表示了一个比较紧致的界, 而小omega表示了一个比较松的界.

总结一下不同的记号:

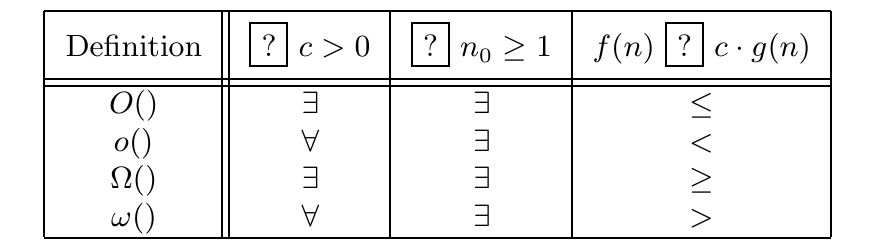
5. Theta Notation (Θ-Notation)

能够同时表示上界和下界. 表示算法的平均意义复杂度(考虑所有输入). 这个也通常表示一个比较紧致的界.

\(f(n) = \Theta(g(n))\): 存在大于0的常数 \(c_1, c_2, n_0\), 使得对于任意的 \(n \geq n_0\), 都有 $ 0 \leq c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n) $.

6. 常用的表示

• 通常用 \(2^{\omega(\log n)}\) 或者 \(n^{\omega(1)}\) 来表示超多项式.

• 超多项式, 但是亚指数(比任何多项式都增长得快, 也比任何指数函数都增长得慢): \(2^{\sqrt n}\), \(n^{\log n}\).

• \({\displaystyle f(n)=\mathrm {O} (g(n))} \iff {\displaystyle g(n)=\mathrm {\Omega} (f(n))}\).

• ${\displaystyle f(n)=\omega (g(n))} \iff \displaystyle g(n)=o(f(n)) $.

• \(f(n) = \Theta(g(n)) \iff f(n) = O(g(n)) \wedge f(n) = \Omega(g(n))\).

参考:

1. https://www2.cs.arizona.edu/classes/cs345/summer14/files/bigO.pdf
2. https://www.geeksforgeeks.org/analysis-of-algorithems-little-o-and-little-omega-notations/
3. https://www.quora.com/What-is-the-intuitive-distinction-between-super-polynomial-growth-and-exponential-growth