为何二叉树如此重要，而不是三叉树四叉树？

为何二叉树如此重要，而不是三叉树四叉树？

性能对比：

• 数组：查找块O(1),增删慢O(n)
• 链表： 查找慢O(n),增删块O(1)
• 二叉搜索树BST： 查找快、增删快。二叉树可以使用二分法算法

平衡二叉树

• BST如果不平衡，那就成了链表了，无法做到最优秀
• 所以要尽量平衡，即平衡二叉搜索树 BBST
• BBST增删查，时间复杂度都是O(logn),即树的高度

总结：

• 数组、链表都各有缺点
• 特定的二叉树，即平衡二叉树BBST 可以让整体效果最优
• 所以我们说二叉树很重要，而不是三叉四叉树，因为无法使用二分算法实现最优解

堆：

　　JS执行时，代码中的变量

• • • 值类型 - 存储到栈里
    • 引用类型 - 存储到堆里

                          

         堆的特点：

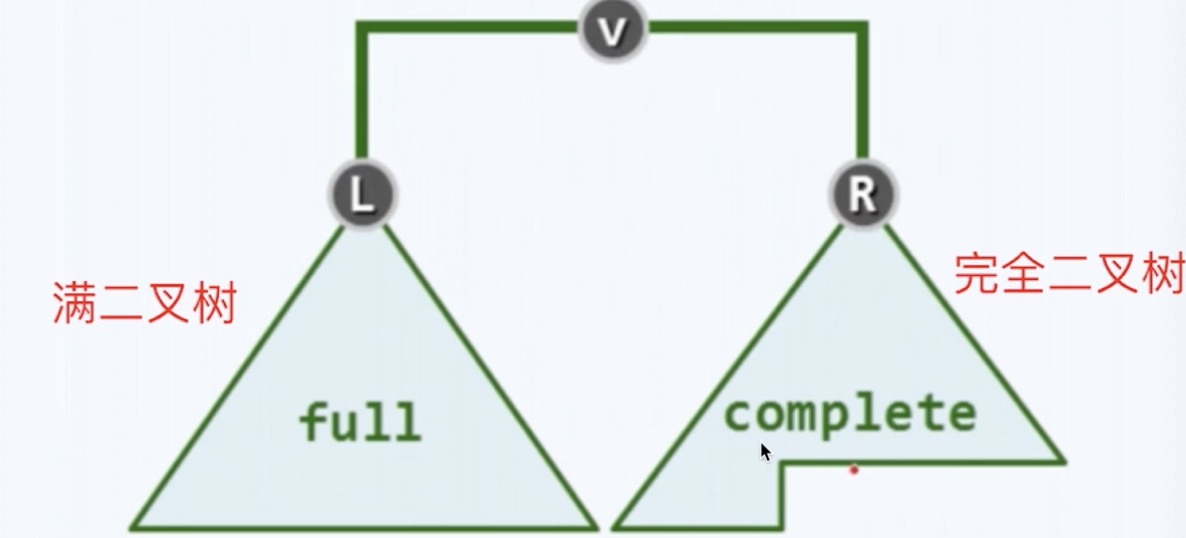
• • • 堆是一个完全二叉树，即如果填不满先保证左边填满。
      • 满二叉树： 树的所有都是填满的
      • 完全二叉树: 如果不能保证都填满，就先让左边填满，右边空着　

　　　　　　　　　　　　

• • • 节点的值，总是不大于（或不小于）其父节点的值
    • 最大堆： 父节点 >= 子节点
    • 最小堆： 父节点 <= 子节点

　　　　　　　　　　

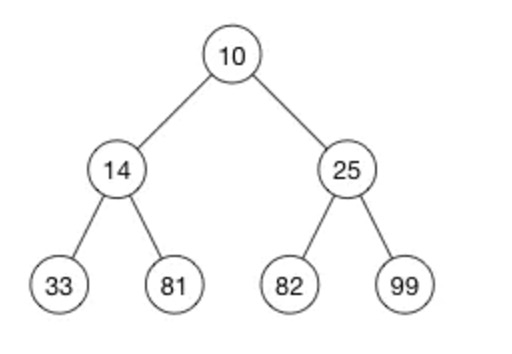
　　　　　　　　　　上图为最小堆，即父节点<= 子节点　　

       堆和搜索二叉树BST 区别：

• • • 堆虽然逻辑上是二叉树，但实际上它使用数组来存储；而BST 是对象：{value,left,right}。
      • 上图的最小堆，用数组来表示

        const heap = [-1,10,14,25,33,81,82,99] // 忽略0 节点

      • 节点关系：根据一个节点的位置i,可以获取到父节点的位置 和 左右两个子节点的位置

        //节点关系
        
        const parentIndex = Math.floor( i/2) 
        const leftIndex = 2 * i 
        const rightIndex = 2* i + 1

        eg: heap 中 元素 25 的索引值为：3；所以 父节点索引值= Math.floor(3 /2) = 1, leftIndex = 2,rightIndex = 3;即 25的父节点和两个子节点分别为：10 33 81

        　　
    • 堆的排序没有BST那么严格（BST必须是左节点比父节点小，右节点比父节点大），所以查询起来比BST 慢
      • 但结合堆的应用场景，一般使用内存地址（栈中已经保存了）来查询，不会直接从根节点开始搜索查询
      • 堆的物理结构是数组，所以查询复杂度就是O(1)　　
    • 堆的增删比BST 快，维持平衡也更快
    • 堆和BST 的时间复杂度都是O(logn),即树的高度　

　　堆的使用场景：　

• • 特别适合“堆栈模型”（比如 JS代码的执行，值类型变量和引用类型变量的存储）
  • 堆的数据，都是在栈中应用的，不需要从root遍历
  • 堆恰巧是数组形式，根据栈的地址，可用O(1)找到目标