时空数据库
时空数据库管理移动对象，比如：汽车、飞机、地貌变化等。空间数据库是时空数据库的特例，即时刻固定。
轨迹压缩
每秒钟都会从 GPS 获取大量 $(x,y,t)$ 格式的数据，如何在不降低物体轨迹精度的前提下减小数据量呢？主要有三个指标：处理时间、压缩率、误差测量。
误差：原始轨迹位置与估计轨迹位置之间的距离。主要有两种误差测量指标：垂直欧式距离、时间同步欧式距离。
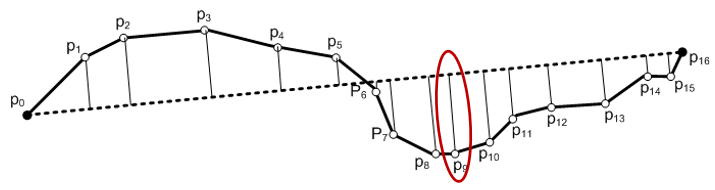
垂直欧式距离：如下左图所示，$p_1,p_7,p_{12}$ 是压缩后的点，垂直度量则为原始轨迹点到压缩后轨迹之间的投影距离。
时间同步欧式距离：如下右图所示，$p_1,p_7,p_{12}$ 作为压缩后的点，假定物体移动的速度恒定，那么 $p_1,p_2$ 之间的时间和 $p_1,p_2^{'}$ 之间的时间相同。
轨迹压缩分为在线压缩和离线压缩两类。
离线压缩：收集完整的轨迹数据后，先压缩再传输至服务器。常用的算法：道格拉斯-普客（DP）算法。
在线压缩：根据要求的精度选择性的在线更新。常用的算法：滑动窗口, 开放窗口。
1. 离线压缩 - DP算法
在估计轨迹中根据垂直欧式距离保留方向趋势，将原始轨迹替换为近似直线段。如果替换不满足指定的误差要求，则通过选择误差最大的位置点作
为分割点，递归地将原问题划分为两个子问题，直到近似轨迹与原始轨迹之间的误差低于指定的误差阈值。
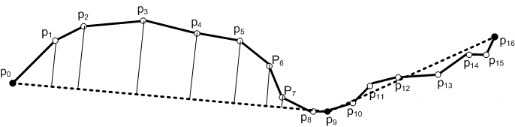
举个例子：下面左图中，估计轨迹是 $p_0$ 和 $p_{16}$，$p_9$ 引入了最大误差，于是切分为 $p_0,p_9$ 和 $p_9,p_{16}$，如下右图。
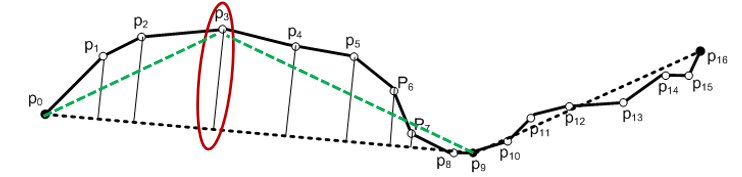
$p_0,p_9$ 中 $p_3$ 又引入了最大误差，因此再将 $p_3$ 作为分割点切开。
2. 在线压缩 - 滑动窗口
用一条有效的线段拟合一个增长的滑动窗口中的位置点，并继续增长滑动窗口，直到近似误差超过某个误差界。
首先将轨迹的第一个点初始化为锚点 $p_0$，然后开始增大滑动窗口，当一个新的点 $p_i$ 加入到滑动窗口中时，用线段 $p_0p_i$ 来拟合滑
动窗口内所有的原始轨迹点。只要窗口内的轨迹相对于线段 $p_ap_i$ 的距离误差小于用户指定的误差阈值，滑动窗口就会继续增大。否则，将
线段 $pap_{i-1}$ 作为近似轨迹的一部分，并将 $p_{i-1} 设置为新的锚点。该算法将一直持续到访问完原始轨迹中的所有位置点。
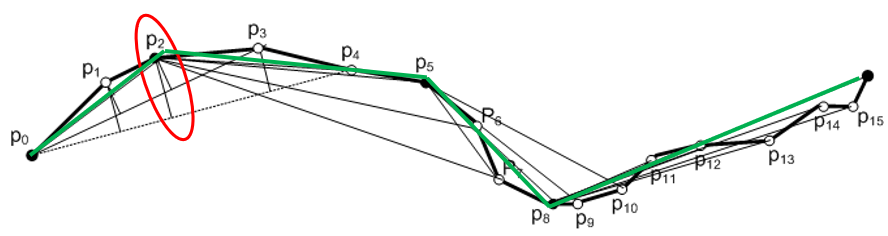
举个例子：当滑动窗口从 $p_0$ 增长到 $p_0,p_1,p_2,p_3$ 时，拟合线段与原始轨迹之间的误差均不大于指定的误差阈值。当包含 $p_4$ 时，
$p_2$ 的误差超过阈值，因此 $p_0p_3$ 被包含在近似轨迹中，然后 $p_3$ 被设置为新的锚点。下图绿线即为最终生成的轨迹。
3. 在线压缩-开放窗口
与滑动窗口不同，开放窗口选择滑动窗口中误差最大的点作为逼近线段的闭合点和新的锚点。当包含 $p_4$ 时，$p_2$ 的误差超过阈值，因此 $p_0p_2$
被包含在近似轨迹中，$p_2$ 被设置为新锚点。
轨迹地图匹配
地图匹配（Map Matching）是指将行车轨迹的经纬度采样序列与数字地图路网匹配的过程，其本质上是平面线段序列的模式匹配问题。
在实际应用中，GPS 采样信号的质量会严重影响地图匹配结果：采样频率的降低、定位误差的加大、信号的丢失，都会使匹配的不准确性增加。
这些情况在实际应用中经常出现。如何在这些情况下仍能保持较高的路径匹配准确率是个值得研究的问题。
局部/增量算法：是贪婪算法，每次确定一个匹配点，下个点从已经确定的匹配点开始。这些方法根据距离和方向相似性来找到局部最优点或边。（在线匹配）
全局算法：是要从路网中找到一条与采样轨迹最接近的匹配轨迹。为了测量采样轨迹和匹配轨迹的相似性，大多数算法使用“Frechet距离”。（离线匹配）
Frechet Distance 用于衡量两个曲线的相似度，后又被描述为遛狗最短狗绳问题，即：主人走路径 $A$，狗走路径 $B$，各自走完这两条路径过程中所需要的最短狗绳长度。
举个例子：下图中黑色折线是人的轨迹，蓝色折线是狗的轨迹，刚开始人和狗都位于位置 $0$，现在让它们往前走，速度可以不同，这里假设人狗速度相同，
也就是说人和狗的距离不会超过 $1$ 个坐标，两者或交替前进或同时前进。我们的目的是用最短的狗绳走完这两条轨迹，橙色表示狗绳。
现在人狗都位于位置 $0$，至少需要的狗绳长度如橙线所示，接下来有三种前进方式：狗先走一步、人先走一步、人狗同时走。观察这三种前进方式狗绳
长度的变化，我们要找出使狗绳长度最短的前进方式。显然狗先走一步，狗绳最短，如下右图，此时人在位置 $0$，狗在位置 $1$。
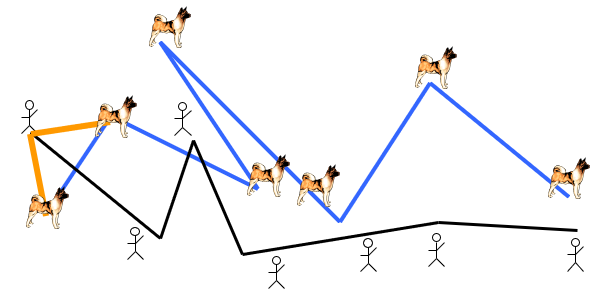
用坐标 $(0,1)$ 表示当前人狗位置，下一步人先走，坐标变为 $(1,1)$，如下左图。下一步，人狗同时走，坐标变为 $(2,2)$，如下右图：
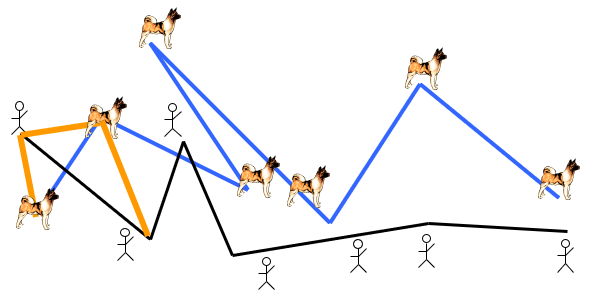
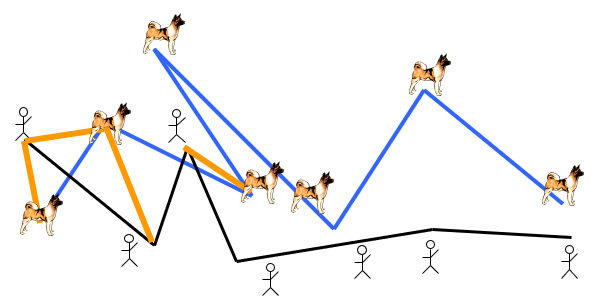
接下来，人先走一步，坐标变为 $(3,2)$，如下左图。因为速度限制，所以接下来只能狗前进，坐标变为 $(3,3)$，如下右图。
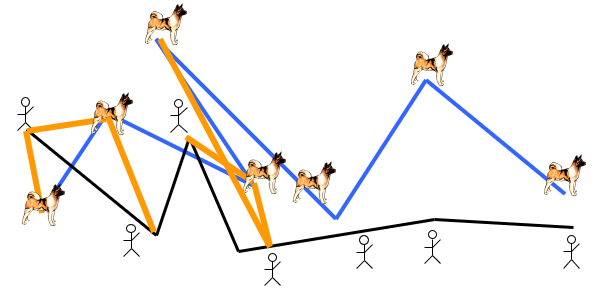
接下来，人狗同时前进，坐标变为 $(4,4)$，如下左图。然后人前进一步，坐标变为 $(5,4)$，如下右图。
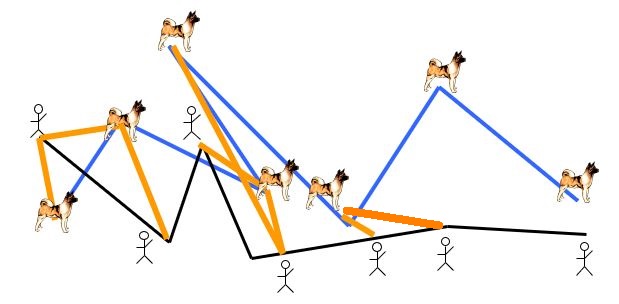
接下来，狗前进一步，坐标变为 $(5,5)$，如下左图。然后人狗同时前进一步，坐标变为 $(6,6)$，如下右图。
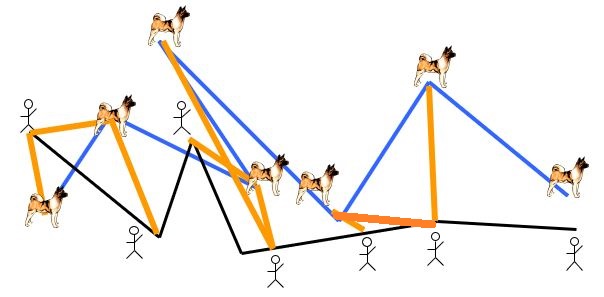
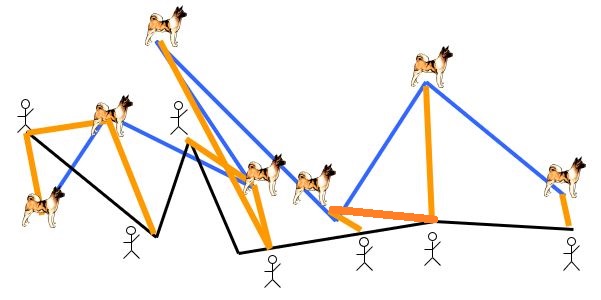
所以最终算法的结果就是下图中红色区域内的狗绳长度，就是最短所需狗绳长度。
递推公式为：
$$dp[i][j] = \max\left \{ \min\left \{ dp[i-1][j], dp[i-1][j-1], dp[i][j-1] \right \},\; E(i,j) \right \}$$
$E(i,j)$ 表示两点之间的欧式距离。这个递推公式是两个对象速度相同的情形(交替前进)，人和狗可以从上面三种情况到达 $i,j$ 点。所以我
们需要找到这三个位置最小的那一个距离与 $i,j$ 点的距离进行比较。
