隐马尔科夫模型
隐马尔科夫模型(Hidden Markov Model,简称HMM)是比较经典的机器学习模型,它在语言识别,自然语言处理,模式识别等领域得到广泛的应用。
随着目前深度学习的崛起,尤其是 RNN, LSTM 等神经网络序列模型的火热,HMM 的地位有所下降。但是作为一个经典的模型,学习 HMM 的模型和对
应算法,有助于提高我们对解决问题建模的能力以及算法思路的拓展。
$HMM$ 模型适用的问题:寻找一个事物在一段时间里的变化模式(规律),比如计算中的指令序列、句子中的词语顺序等。
假设 $Q$ 是所有可能的隐藏状态的集合,$V$ 是所有可能的观测状态的集合,即:
$$Q = \left \{ q_{1},q_{2},\cdots,q_{n} \right \} \\
V = \left \{ v_{1},v_{2},\cdots,v_{m} \right \}$$
其中,$n$ 是所有可能的隐藏状态数,$m$ 是所有可能的观察状态数,$Q$ 的每个元素值依次为 $1$ 到 $n$,$V$ 的每个元素值依次为 $1$ 到 $m$,即 $q_{i} = i,v_{k} = k$。
对于一个长度为 $T$ 的序列,$I$ 是状态序列, $O$ 是观察序列,即
$$I = \left \{ i_{1},i_{2},\cdots,i_{T} \right \}, \; i_{t} \in Q \\
O = \left \{ o_{1},o_{2},\cdots,o_{T} \right \}, \; o_{t} \in V$$
每个元素都是数字,每个元素的下标代表时刻,也就是说:状态序列和观察序列的元素都是有先后关系的。
状态转移矩阵 $A$:包含了一个隐藏状态到另一个隐藏状态的概率,每个元素表示一个条件概率,是不同时刻的状态转换。
$$A = \begin{bmatrix}
a_{ij}
\end{bmatrix}_{n \times n} \\
a_{ij} = P(i_{t+1} = q_{j} | i_{t} = q_{i}),\; i = 1,2,\cdots,n;\; j = 1,2,\cdots,n$$
观测概率矩阵 $B$:包含了一个隐藏状态到一个观察状态的概率,每个元素表示一个条件概率,是同一时刻的状态转换。
$$B = \begin{bmatrix}
b_{jk}
\end{bmatrix}_{n \times m} \\
b_{jk} = P(o_{t} = v_{k} | i_{t} = q_{j}),\; j = 1,2,\cdots,n;\; k = 1,2,\cdots,m$$
由定义的两个条件概率矩阵可知,$HMM$ 模型做了两个假设:
1)马尔科夫链假设:任意时刻的隐藏状态只依赖于它前一个隐藏状态。这样假设有点极端,因为很多时候我们的某一个隐藏状态不仅仅只
依赖于前一个隐藏状态,可能是前两个或者是前三个。但是这样假设的好处就是模型简单,便于求解。用数学式子表达为
$$P(i_{t} | i_{1},i_{2},\cdots,i_{t-1}) = P(i_{t} | i_{2},\cdots,i_{t-1}) = \cdots = P(i_{t} | i_{t-1},i_{t-2}) = P(i_{t} | i_{t-1})$$
2)观测独立性假设:任意时刻的观察状态只依赖于当前时刻的隐藏状态,这也是一个为了简化模型的假设。用数学式子表达为
$$P(o_{t} | i_{1},i_{2},\cdots,i_{t}) = P(o_{t} | i_{2},\cdots,i_{t}) = P(o_{t} | i_{t})$$
除此之外,还需要一组在时刻 $t=1$ 的隐藏状态概率分布 $\Pi$,是一个 $n$ 维度向量,每个元素表示 $t = 1$ 时刻处于某个状态的概率。
$$\Pi = \begin{bmatrix}
\pi_{i}
\end{bmatrix}_{n} \\
\pi_{i} = P(i_{1} = q_{i}), i = 1,2,\cdots,n$$
因为 $q_{i}$ 的数值就是等于 $i$,所以 $i_{1}$ 取 $q_{i}$ 的概率就是 $\pi_{q_{i}}$。
一个 $HMM$ 模型,可以由隐藏状态初始概率分布 $\Pi$, 状态转移概率矩阵 $A$ 和观测状态概率矩阵 $B$ 决定。$\Pi,A$ 决定状态序列,$B$ 决定
观测序列。因此,$HMM$ 模型可以由一个三元组 $\lambda$ 表示如下:
$$\lambda = (A,B,\Pi)$$
总之:每个观察值由同一时刻的状态值决定,每个状态值由前一时刻的状态值决定。
评估观察序列概率
已知 $HMM$ 模型的参数 $\lambda = (A,B,\Pi)$。其中 $A$ 是隐藏状态转移概率的矩阵,$B$ 是观测状态生成概率的矩阵, $\Pi$ 是隐藏状态的初始概率分布。
同时我们也已经得到了观测序列 $O={o_{1},o_{2},...o_{T}}$,现在我们要求观测序列 $O$ 在模型 $\lambda$ 下出现的条件概率 $P(O|\lambda)$。
1. 直接计算法
状态序列 $I = \left \{ i_{1},i_{2},\cdots,i_{T} \right \}$ 发生的概率为(序列元素为状态的索引号):
$$P(I|\lambda) = \pi_{i_{1}}a_{i_{1}i_{2}}a_{i_{2}i_{3}} \cdots a_{i_{T-1}i_{T}}$$
固定这个状态序列,输出观察序列 $O = \left \{ o_{1},o_{2},\cdots,o_{T} \right \}$ 的概率为
$$P(O|I,\lambda) = b_{i_{1}o_{1}}b_{i_{2}o_{2}} \cdots b_{i_{T}o_{T}}$$
则 $O$ 和 $I$ 联合出现的概率是:
$$P(O,I|\lambda) = P(I|\lambda)P(O|I,\lambda) = \pi_{i_{1}}b_{i_{1}o_{1}} \cdot a_{i_{1}i_{2}}b_{i_{2}o_{2}} \cdots a_{i_{T-1}i_{T}}b_{i_{T}o_{T}}$$
然后求边缘概率分布,即可得到观测序列 $O$ 在模型 $\lambda$ 下出现的条件概率:
$$P(O|\lambda) = \sum_{I}^{}P(O,I|\lambda)$$
虽然上述方法有效,但是如果我们的隐藏状态数 $n$ 非常多的话就很麻烦,此时我们 $I$ 就有 $n^{T}$ 种组合,算法的时间复杂度是 $O(Tn^{T})$ 阶的。
这里的观察序列是给定的,每个元素都是已知的。
2. 前向算法
引入前向概率:定义到时刻 $t$ 的部分观测序列为 $o_{1},o_{2},\cdots,o_{t}$ 且隐藏状态为 $q_{i}$ 的概率为前向概率,记作
$$\alpha_{t}(i) = P(o_{1},o_{2}, \cdots, o_{t}, i_{t} = q_{i} | \lambda)$$
$\alpha$ 的下标 $t$ 表示到时刻 $t$,参数 $i$ 表示时刻 $t$ 的隐藏状态是 $q_{i}$。
前向算法相当于自低向上的迭代过程。现在我们需要为下面两个式子建立联系:
$$\left\{\begin{matrix}
\alpha_{t}(j) = P(o_{1},o_{2}, \cdots, o_{t}, i_{t} = q_{j} | \lambda) \\
\alpha_{t+1}(i) = P(o_{1},o_{2}, \cdots, o_{t},o_{t+1}, i_{t+1} = q_{i} | \lambda)
\end{matrix}\right.$$
因为 $o_{t+1}$ 由 $i_{t+1}$ 决定,所以先来看下在 $\alpha_{t}(j)$ 的基础上,隐藏状态转为 $i_{t+1}$ 的概率。根据全概率公式有
$$P(o_{1},o_{2}, \cdots, o_{t}, i_{t+1} = q_{i} | \lambda) \\
= \sum_{q_{j}}^{}P(o_{1},o_{2}, \cdots, o_{t},i_{t}=q_{j},i_{t+1} = q_{i} | \lambda) \\
= \sum_{q_{j}}^{}P(o_{1},o_{2}, \cdots, o_{t},i_{t}=q_{j}|\lambda)P(i_{t+1} = q_{i} |o_{1},o_{2}, \cdots, o_{t},i_{t}=q_{j}, \lambda) \\
= \sum_{j = 1}^{n}\alpha_{t}(j) \cdot a_{ji}$$
进一步地
$$\alpha_{t+1}(i) = P(o_{1},o_{2}, \cdots, o_{t},o_{t+1},i_{t+1} = q_{i} | \lambda) \\
= P(o_{1},o_{2}, \cdots, o_{t}, i_{t+1} = q_{i} | \lambda)P(o_{t+1} | o_{1},o_{2}, \cdots, o_{t}, i_{t+1} = q_{i}, \lambda) \\
= \left [\sum_{j = 1}^{n}\alpha_{t}(j) \cdot a_{ji} \right ] \cdot b_{i,o_{t+1}}$$
再根据全概率公式得
$$P(O|\lambda) = P(o_{1},o_{2}, \cdots, o_{T} | \lambda) \\
= \sum_{q_{j}}^{}P(o_{1},o_{2}, \cdots, o_{T},i_{T} = q_{j} | \lambda) \\
= \sum_{j=1}^{n}\alpha_{T}(j)$$
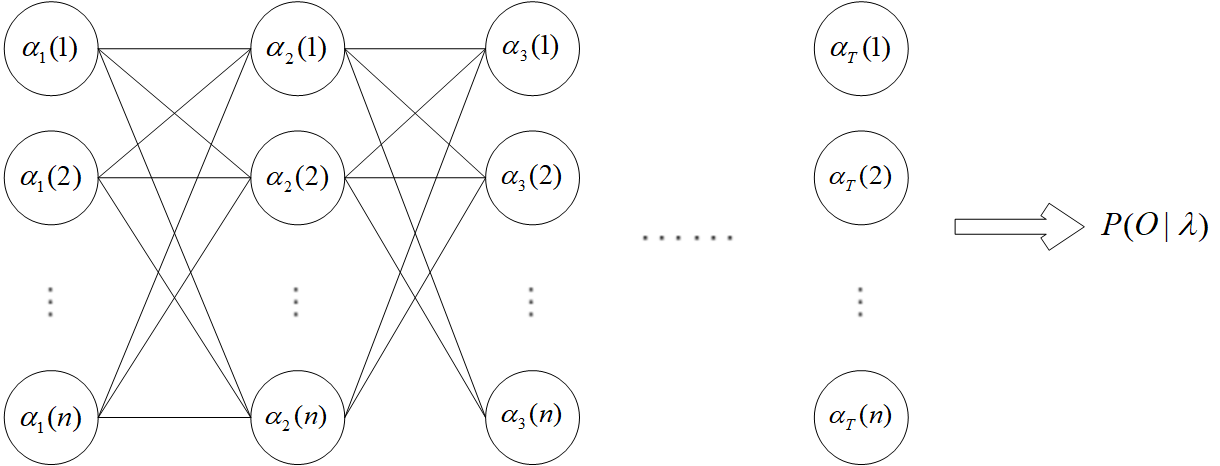
由图可以看出,此时的时间复杂度为 $O(Tn^{2})$。
3. 后向算法
引入后向概率:定义在时刻 $t$ 隐藏状态为 $q_{i}$ 的条件下,从 $t+1$ 到 $T$ 的部分观测序列为 $o_{t+1},o_{t+2},\cdots,o_{T}$ 的概率为后向概率,记作
$$\beta_{t}(i) = P(o_{t+1},o_{t+2},\cdots,o_{T} | i_{t} = q_{i},\lambda)$$
与前向概率不同的是,这个式子只包含了 $t$ 时刻的隐藏状态,而没有包含 $t$ 时刻的输出 $o_{t}$,现在我们需要为下面两个式子建立联系:
$$\left\{\begin{matrix}
\beta_{t}(i) = P(o_{t+1},o_{t+2},\cdots,o_{T} | i_{t} = q_{i},\lambda) \\
\beta_{t+1}(j) = P(o_{t+2},o_{t+3}, \cdots,o_{T}| i_{t+1} = q_{j},\lambda)
\end{matrix}\right.$$
无论是状态矩阵还是观测矩阵,概率都是从前往后推导的,所以这里也从前往后推,根据全概率公式有
$$\beta_{t}(i) = P(o_{t+1},o_{t+2},\cdots,o_{T} | i_{t} = q_{i},\lambda) \\
= \sum_{q_{j}}^{}P(o_{t+1},o_{t+2},\cdots,o_{T},i_{t+1} = q_{j} | i_{t} = q_{i},\lambda) \\
= \sum_{j=1}^{n}P(o_{t+1},o_{t+2},\cdots,o_{T} | i_{t+1} = q_{j},i_{t} = q_{i},\lambda) \cdot P(i_{t+1} = q_{j} | i_{t} = q_{i},\lambda) \\
= \sum_{j=1}^{n}P(o_{t+1},o_{t+2},\cdots,o_{T} | i_{t+1} = q_{j},i_{t} = q_{i},\lambda) \cdot a_{ij}$$
由观测独立性假设可知,$o_{t+1}$ 只与 $i_{t+1}$ 有关,和 $i_{t}$ 无关,当然 $o_{t+2},o_{t+3},...,o_{T}$ 与 $i_{t}$ 更没有关系了,所以
$$\beta_{t}(i) = \sum_{j=1}^{n}P(o_{t+1},o_{t+2},\cdots,o_{T} | i_{t+1} = q_{j},\lambda) \cdot a_{ij} \\
= \sum_{j=1}^{n}P(o_{t+1} | o_{t+2},\cdots,o_{T},i_{t+1} = q_{j},\lambda) \cdot P(o_{t+2},\cdots,o_{T} | i_{t+1} = q_{j},\lambda) \cdot a_{ij}$$
还是因为 $o_{t+1}$ 只与 $i_{t+1}$ 有关,所以
$$\beta_{t}(i) = \sum_{j=1}^{n}P(o_{t+1} | i_{t+1} = q_{j},\lambda) \cdot P(o_{t+2},\cdots,o_{T} | i_{t+1} = q_{j},\lambda) \cdot a_{ij} \\
= \sum_{j=1}^{n}b_{j,o_{t+1}} \cdot \beta_{t+1}(j) \cdot a_{ij}$$
这里只是数学上纯逻辑的推导,感觉很难记忆和理解。
$\bullet$ 考虑 $\alpha_{t}(i) \beta_{t}(i)$
$$\alpha_{t}(i)\beta_{t}(i) = P(o_{1},o_{2}, \cdots, o_{t}, i_{t} = q_{i} | \lambda) P(o_{t+1},o_{t+2},\cdots,o_{T} | i_{t} = q_{i},\lambda) \\
= P(i_{t} = q_{i})P(o_{1},o_{2}, \cdots, o_{t} | i_{t} = q_{i}, \lambda) P(o_{t+1},o_{t+2},\cdots,o_{T} | i_{t} = q_{i},\lambda) \\
= P(i_{t} = q_{i})P(o_{1},o_{2}, \cdots, o_{t},o_{t+1},o_{t+2},\cdots,o_{T} | i_{t} = q_{i}, \lambda) \\
= P(o_{1},o_{2},\cdots,o_{T},i_{t} = q_{i} | \lambda)$$
学习算法
给定训练数据为长度为 $T$ 的观测序列 $O = \left \{ o_{1},o_{2},\cdots,o_{T} \right \}$,而没有对应的状态序列,目标是学习隐马尔科夫模型的参数 $\lambda = (A,B,\pi)$。
将观测不到的隐藏数据记为 $I = \left \{ i_{1},i_{2},\cdots,i_{T} \right \}$,那么马尔可夫模型事实上就是一个含有隐变量的概率模型:
$$P(O|\lambda) = \sum_{I}^{}P(O,I|\lambda)$$
这里的 $\sum_{I}^{}$ 表示遍历所有隐藏序列 $I$ 的可能取值。可以通过 $EM$ 算法来求解参数。我们需要最大化的似然函数为
$$L(\lambda,\lambda_{j}) = \sum_{I}^{}P(I|O,\lambda_{j})\ln P(O,I|\lambda)$$
在 $M$ 步我们要极大化上式,得到一个 $\lambda_{j+1}$。计算联合分布 $P(O,I|\lambda)$ 的表达式如下:
$$P(O,I|\lambda) = \left (\pi_{i_{1}}b_{i_{1}o_{1}} \right ) \cdot \left (a_{i_{1}i_{2}}b_{i_{2}o_{2}} \right ) \cdots \left (a_{i_{T-1}i_{T}}b_{i_{T}o_{T}} \right )$$
由于
$$P(I|O,\lambda_{j}) = \frac{P(I,O|\lambda_{j})}{P(O|\lambda_{j})}$$
而 $P(O|\lambda_{j})$ 是常数,因此我们要极大化的式子等价于:
$$L(\lambda,\lambda_{j}) = \sum_{I}^{}P(O,I|\lambda_{j})\ln P(O,I|\lambda)$$
将联合分布表达式代入得
$$L(\lambda,\lambda_{j}) = \sum_{I}^{}P(O,I|\lambda_{j}) \left (\ln \pi_{i_{1}} + \sum_{t = 1}^{T-1}\ln a_{i_{t}i_{t+1}} + \sum_{t = 1}^{T}\ln b_{i_{t}o_{t}} \right ) \\
= \sum_{I}^{}\ln \pi_{i_{1}} \cdot P(O,I|\lambda_{j}) + \sum_{I}^{}\left ( \sum_{t = 1}^{T-1}\ln a_{i_{t}i_{t+1}} \right )P(O,I|\lambda_{j}) + \sum_{I}^{}\left ( \sum_{t = 1}^{T}\ln b_{i_{t}o_{t}} \right )P(O,I|\lambda_{j})$$
这个式子有 $3$ 项,只需对各项分别极大化。
1)第一项可以写成:
$$\sum_{I}^{}\ln \pi_{i_{1}} \cdot P(O,I|\lambda_{j}) = \sum_{i_{1}}^{}\sum_{i_{2},i_{3},\cdots,i_{T}}^{}\ln \pi_{i_{1}} \cdot P(O,i_{1},i_{2},i_{3},\cdots,i_{T} | \lambda_{j}) \\
= \sum_{i_{1}}^{} \ln \pi_{i_{1}} \cdot P(O,i_{1} | \lambda_{j}) \\
= \sum_{i = 1}^{n} \ln \pi_{i} \cdot P(O,i_{1} = i | \lambda_{j})$$
其中 $n$ 为可能的隐藏状态数,由于
$$\sum_{i = 1}^{n}\pi_{i} = 1$$
根据拉格朗日子乘法,得到要极大化的拉格朗日函数为:
$$\sum_{i = 1}^{n} \ln \pi_{i} \cdot P(O,i_{1} = i | \lambda_{j}) + \gamma \left ( \sum_{i = 1}^{n}\pi_{i} - 1 \right )$$
上式对 $\pi_{i}$ 求偏导数并令结果为0, 可解得
$$\pi_{i} = \frac{P(O,i_{1} = i | \lambda_{j})}{P(O | \lambda_{j})}$$
2)第二项可以写成:
$$\sum_{I}^{}\left ( \sum_{t = 1}^{T-1}\ln a_{i_{t}i_{t+1}} \right )P(O,I|\lambda_{j})
= \sum_{I}^{}\sum_{t = 1}^{T-1}\ln a_{i_{t}i_{t+1}}P(O,I|\lambda_{j})
= \sum_{t = 1}^{T-1}\sum_{I}^{}\ln a_{i_{t}i_{t+1}}P(O,I|\lambda_{j}) \\
= \sum_{t = 1}^{T-1}\sum_{i_{t}}^{}\sum_{i_{t+1}}^{}\sum_{(i_{1},\cdots,i_{t-1},i_{t+2},\cdots,i_{T})}^{}\ln a_{i_{t}i_{t+1}}P(O,i_{1},\cdots,i_{t-1},i_{t},i_{t+1}i_{t+2},\cdots,i_{T} | \lambda_{j} \\
= \sum_{t = 1}^{T-1}\sum_{i_{t}}^{}\sum_{i_{t+1}}^{}\ln a_{i_{t}i_{t+1}}P(O,i_{t},i_{t+1} | \lambda_{j}) \\
= \sum_{t = 1}^{T-1}\sum_{i=1}^{n}\sum_{j=1}^{n}\ln a_{ij}P(O,i_{t},i_{t+1} | \lambda_{j})$$
由于
$$\sum_{i = 1}^{n}a_{ij} = 1$$
建立拉格朗日函数可解得
$$a_{ij} = \frac{\sum_{t = 1}^{T-1}P(O,i_{t}=i,i_{t+1}=j | \lambda_{j})}{\sum_{t = 1}^{T-1}P(O,i_{t}=i | \lambda_{j})}$$
3)第三项可以写成:
$$\sum_{I}^{}\left ( \sum_{t = 1}^{T}\ln b_{i_{t}o_{t}} \right )P(O,I|\lambda_{j}) = \sum_{I}^{}\sum_{t = 1}^{T}\ln b_{i_{t}o_{t}}P(O,I|\lambda_{j}) = \sum_{t = 1}^{T}\sum_{I}^{}\ln b_{i_{t}o_{t}}P(O,I|\lambda_{j})\\
= \sum_{t = 1}^{T}\sum_{i_{t}}^{}\sum_{(i_{1},\cdots,i_{t-1},i_{t+1},\cdots,i_{T})}^{}\ln b_{i_{t}o_{t}} P(O,i_{1},\cdots,i_{t-1},i_{t},i_{t+1},\cdots,i_{T}|\lambda_{j}) \\
= \sum_{t = 1}^{T}\sum_{i_{t}}^{}\ln b_{i_{t}o_{t}}P(O,i_{t} | \lambda_{j}) \\
= \sum_{t = 1}^{T}\sum_{j=1}^{n}\ln b_{j,o_{t}}P(O,i_{t} = j | \lambda_{j})$$
建立拉格朗日函数求解得
$$b_{jk} = \frac{\sum_{i=1}^{T}P(O,i_{t}=j | \lambda_{j})I(o_{t} = v_{k})}{\sum_{i=1}^{T}P(O,i_{t}=j | \lambda_{j})}$$
维特比算法
在 $HMM$ 模型的解码问题中,给定模型 $\lambda=(A,B,\Pi)$ 和观测序列 $O = \left \{ o_{1},o_{2},...,o_{T} \right \}$,求给定观测序列 $O$ 条件下,最可能出现的对应的状态序
列 $I^{*} = \left \{ i_{1}^{∗},i_{2}^{*},...,i_{T}^{*} \right \}$,即 $P(I^{*}|O)$ 要最大化。
维特比算法定义了两个局部状态用于递推:
1)第一个局部状态是在时刻 $t$ 隐藏状态为 $i$ 所有可能的状态转移路径 $i_{1},i_{2},...,i_{t}$ 中的概率最大值。记为 $\delta_{t}(i)$,即
$$\delta_{t}(i) = \max P(i_{1},i_{2},\cdots,i_{t-1},i_{t} = i,o_{1},o_{2},\cdots,o_{t} | \lambda), i = 1,2,\cdots,n$$
同一时刻,需要计算得到 $n$ 个概率,即得到 $\delta_{t}(1),\delta_{t}(2),...,\delta_{t}(n)$,因为一共有 $T$ 个时刻,所以这样的概率需要计算 $nT$ 个。
相邻时刻概率间的递推公式为
$$\delta_{t+1}(j) = \max_{1 \leq i \leq n}\left [\delta_{t}(i)a_{ij} \right ]b_{j,o_{t+1}}, \; j = 1,2,\cdots,n$$
怎么理解呢?如下图:
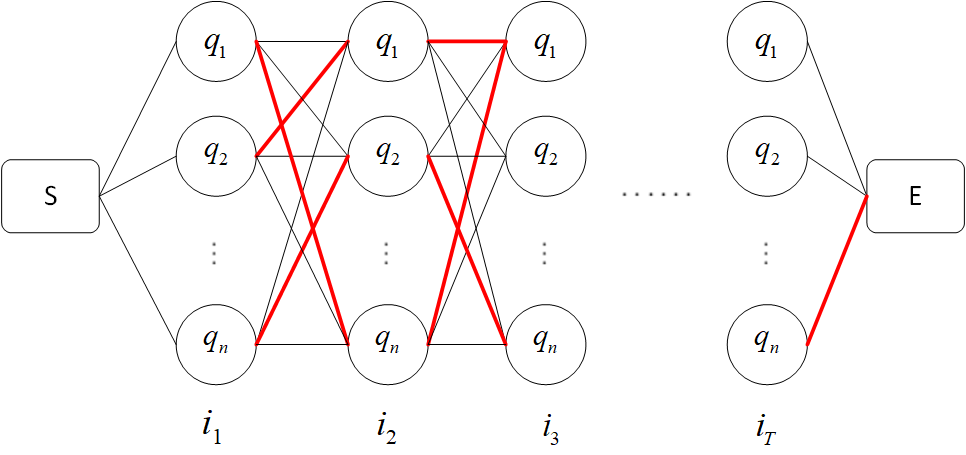
我们的目标是要在 $S$ 和 $E$ 之间找一条能使 $P(I^{*}|O)$ 最大的路径,从 $S$ 开始($0$ 时刻)从左到右一列一列地来看。
a. 从 $0$ 时刻到 $1$ 时刻,有 $n$ 种可能,即状态 $i_{1}$ 的取值有 $n$ 个可能,此时没办法判断哪个状态会是结果路径中的一部分。
b. 从 $1$ 时刻到 $2$ 时刻,当 $i_{2} = q_{1}$ 时,从到达这个结点的 $n$ 条连线中,分别计算如下概率
$$\pi_{1}a_{11} \\
\pi_{2}a_{21} \\
\vdots \\
\pi_{n}a_{n1}$$
肯定可以找出最大的那个概率,假如对应图中红色连接线,即当 $i_{1} = q_{2}$ 时,$P(i_{1},i_{2} = q_{1},o_{1},o_{2})$ 最大。
同理,当 $i_{2} = q_{2}$ 时,也对应一个 $i_{1} = q_{n}$ 使概率最大,依此类推,在 $t = 1$ 到 $t = 2$ 之间可以找到 $n$ 条红色连接线。
这便是维特比算法的重点,本来在时刻 $1$ 和时刻 $2$ 之间存在 $n^{2}$ 条路径,现在变成了 $n$ 条,因为只有红色路径才可能是全局最优路径
的一部分,这就有点像最短路径算法,可以通过反证法证明。
c. 从 $2$ 时刻到 $3$ 时刻,也可以找到 $n$ 条红色路径,直接在已经得到的 $\delta_{2}(1),\delta_{2}(2),...,\delta_{2}(n)$ 的基础上计算。即递推公式所展示的那样。
2)第二个局部状态由第一个局部状态递推得到。我们定义在时刻 $t$ 隐藏状态为 $i$ 的所有单个状态转移路径 $(i_{1},i_{2},...,i_{t-1},i_{t}=i)$ 中概率最大
的转移路径中第 $t−1$ 个节点的隐藏状态为 $\psi_{t}(i)$,其递推表达式可以表示为:
$$\psi_{t}(i) = \max_{1 \leq j \leq n}\left [\delta_{t-1}(j)a_{ji} \right ]$$
其实就是保存了到达该结点的前一个结点。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号