机器学习-聚类-谱聚类算法笔记

 在学习谱聚类算法之前，首先复习一下：实对称阵的特征值是实数

实对称阵不同特征值的特征向量正交

令实对称矩阵为A，其两个不同的特征值λ₁λ₂对应的特征向量分别是μ₁μ₂；

λ₁λ₂ μ₁μ₂都是实数或是实向量。

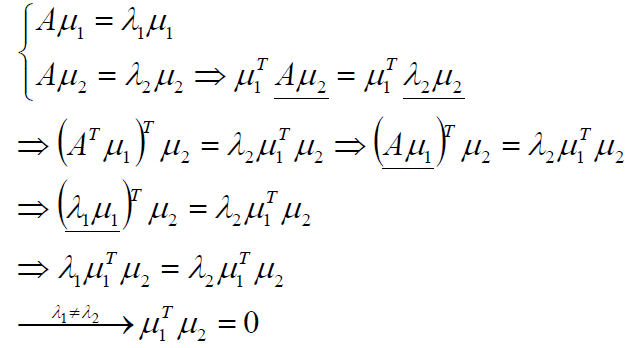
正式介绍谱聚类

　　谱和谱聚类

　　方阵作为线性算子，它的所有特征值的全体统称方阵的谱。
　　方阵的谱半径为最大的特征值
　　矩阵A的谱半径：(A^TA)的最大特征值
　谱聚类是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从而达到对样本数据聚类的目的。

　　谱分析的整体过程　　

　　1.给定一组数据x₁,x₂,...x_n，记任意两个点之间的相似度(―距离”的减函数)为s_ij=<x_i,x_j>，形成相似度图(similarity graph)：G=(V,E) 。如果xi和xj之间的相似度sij大于一定的阈值，那么，两个点是连接的，权值记做s_ij。
　2.接下来，可以用相似度图来解决样本数据的聚类问题：找到图的一个划分，形成若干个组(Group)，使得不同组之间有较低的权值，组内有较高的权值。

　　谱聚类一：无向权重图

　　由于谱聚类是基于图论的，因此我们首先温习下图的概念。对于一个图G，我们一般用点的集合V和边的集合E来描述。即为G(V,E)。其中V即为我们数据集里面所有的点(v₁,v₂,...v_n)。对于V中的任意两个点，
可以有边连接，也可以没有边连接。我们定义权重wij为点vi和点vj之间的权重。由于我们是无向图，所以w_ij=w_ji。

　　对于有边连接的两个点v_i和v_j，w_ij>0,对于没有边连接的两个点v_i和v_j，w_ij=0。对于图中的任意一个点v_i，它的度d_i定义为和它相连的所有边的权重之和，即

　　

　　利用每个点度的定义，我们可以得到一个nxn的度矩阵D,它是一个对角矩阵，只有主对角线有值，对应第i行的第i个点的度数。

　　利用所有点之间的权重值，我们可以得到图的邻接矩阵W，它也是一个nxn的矩阵，第i行的第j个值对应我们的权重w_ij。

　　子图A的指示向量：

　　

　　A和B是图G的不相交子图，则定义子图的连接权：

 　　

　　谱聚类二：相似度图G的建立方法

　　邻接矩阵W，它是由任意两点之间的权重值w_ij组成的矩阵。通常我们可以自己输入权重，但是在谱聚类中，我们只有数据点的定义，并没有直接给出这个邻接矩阵，那么怎么得到这个邻接矩阵呢？

　　基本思想是，距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，不过这仅仅是定性，我们需要定量的权重值。一般来说，我们可以通过样本点距离度量的相似矩阵S来获得邻接矩阵W。

　   构建邻接矩阵W的方法有三类。全连接法，ϵ-邻近法和K邻近法。

 　　1）全连接法

　　全连接法构建的邻接矩阵W的所有点之间的权重值都大于0，可以选择不同的核函数来定义边权重，常用的有多项式核函数，高斯核函数和Sigmoid核函数。最常用的是高斯核函数RBF，此时相似矩阵和邻接矩阵相同：

　　　　

　　在实际的应用中，使用全连接法来建立邻接矩阵中使用高斯径向核RBF是最普遍的。

　　2）对于ϵ-邻近法，它设置了一个距离阈值ϵ，然后用欧式距离s_ij度量任意两点xi和xj的距离。即相似矩阵的s_ij=||x_i−x_j||²,  然后根据s_ij和ϵ的大小关系，来定义邻接矩阵W如下：

　　　　

　　从上式可见，两点间的权重要不就是ϵ,要不就是0，没有其他的信息了。距离远近度量很不精确，因此在实际应用中，我们很少使用ϵ-邻近法。

　　3）K邻近法，利用KNN算法遍历所有的样本点，取每个样本最近的k个点作为近邻，只有和样本距离最近的k个点之间的w_ij>0。但是这种方法会造成重构之后的邻接矩阵W非对称，我们后面的算法需要对称邻接矩阵。为了解决这种问题，一般采取下面两种方法之一：

　　第一种K邻近法是只要一个点在另一个点的K近邻中，则保留s_ij

　　

　　第二种K邻近法是必须两个点互为K近邻中，才能保留s_ij

　　

　　构建邻接矩阵W的方法总结

　　ε近邻图：ε=0.3，“月牙部分”非常紧的连接了，但“高斯部分”很多都没连接。当数据有不同的“密度”时，往往发生这种问题。
    k近邻图：可以解决数据存在不同密度时有些无法连接的问题，甚至低密度的“高斯部分”与高密度的“月牙部分”也能够连接。同时，虽然两个“月牙部分”的距离比较近，但k近邻还可以把它们区分开。
   互k近邻图：它趋向于连接相同密度的部分，而不连接不同密度的部分。这种性质介于ε近邻图和k近邻图之间。如果需要聚类不同的密度，这个性质非常有用。
    全连接图：使用高斯相似度函数可以很好的建立权值矩阵。但缺点是建立的矩阵不是稀疏的。
    总结：首先尝试使用k近邻图。

　　谱聚类三：拉普拉斯矩阵

　　拉普拉斯矩阵：L = D – W

　　

　　拉普拉斯矩阵是半正定的，且对应的n个实数特征值都大于等于0，即0=λ1≤λ2≤...≤λn， 且最小的特征值为0。

　　拉普拉斯矩阵的定义：　

　　计算点之间的邻接相似度矩阵W
   　　1）若两个点的相似度值越大，表示这两个点越相似；
   　　2）同时，定义w_ij=0表示v_i,v_j两个点没有任何相似性(无穷远)
  W的第i行元素的和为v_i的度。形成顶点度对角阵D
 　　 1）d_ii表示第i个点的度
 　　 2）除主对角线元素，D其他位臵为0
 未正则的拉普拉斯矩阵：L=D-W
 正则拉普拉斯矩阵
　　 1) 对称拉普拉斯矩阵

　　　　
 　　2) 随机游走拉普拉斯矩阵

　　　　

　　未正则拉普拉斯矩阵算法流程:　

　　　输入：n个点{p_i}，簇的数目k
　　计算n×n的相似度矩阵W和度矩阵D；
　　计算拉普拉斯矩阵L=D-W；
　　计算L的前k个特征向量u₁,u₂,...,u_k；
　　将k个列向量u₁,u₂,...,u_k组成矩阵U，U∈R^n×k；
　　对于i=1,2,...,n,令yi∈R^k是U的第i行的向量；
　　使用k-means算法将点(y_i)_i=1,2,...,n聚类成簇C₁,C₂,...C_k；
　　输出簇A₁,A₂,...A_k，其中，A_i={j|y_j∈C_i}

　　随机游走拉普拉斯矩阵算法流程：

    　　输入：n个点{p_i}，簇的数目k
　　计算n×n的相似度矩阵W和度矩阵D；
　　计算正则拉普拉斯矩阵L_rw=D^-1(D-W)；
　　计算L_rw的前k个特征向量u₁,u₂,...,u_k；
　　将k个列向量u₁,u₂,...,u_k组成矩阵U，U∈ R^n×k ；
　　对于i=1,2,...,n,令y_i∈R^k是U的第i行的向量；
　　使用k-means算法将点(y_i)_i=1,2,...,n聚类成簇C₁,C₂,...C_k ；
　　输出簇A₁,A₂,...A_k，其中，A_i={j|y_j∈C_i}

　　对称拉普拉斯矩阵算法流程:

    　　输入：n个点{p_i}，簇的数目k
　　计算n×n的相似度矩阵W和度矩阵D；
　　计算正则拉普拉斯矩阵L_sym=D^-1/2(D-W) D^-1/2；
　　计算L_sym的前k个特征向量u₁,u₂,...,u_k；
　　将k个列向量u₁,u₂,...,u_k组成矩阵U，U∈R^n×k；
　　对于i=1,2,...,n,令yi∈R^k是U的第i行的向量；
　　对于i=1,2,...,n,将yi∈R^k依次单位化，使得|y_i|=1；
　　使用k-means算法将点(y_i)_i=1,2,...,n聚类成簇C₁,C₂,...C_k；
　　输出簇A₁,A₂,...A_k，其中，A_i={j|y_j∈C_i}

　　随机游走和拉普拉斯矩阵的关系：

　　图论中的随机游走是一个随机过程，它从一个顶点跳转到另外一个顶点。谱聚类即找到图的一个划分，使得随机游走在相同的簇中停留而几乎不会游走到其他簇。

 转移矩阵：从顶点vi跳转到顶点vj的概率正比于边的权值w_ij

　　

　　关于谱聚类的思考

　　谱聚类中的K如何确定？

　　
　最后一步K-Means的作用是什么？
　答：目标函数是关于子图划分指示向量的函数，该向量的值根据子图划分确定，是离散的。该问题是NP的，转换成求连续实数域上的解，最后用K-Means算法离散化。
　未正则/对称/随机游走拉普拉斯矩阵，首选哪个？
　答：随机游走拉普拉斯矩阵
　谱聚类可以用切割图/随机游走/扰动论等解释。

标签传递算法

对于部分样本的标记给定，而大多数样本的标记未知的情形，是半监督学习问题。
标签传递算法(Label Propagation Algorithm,LPA)，将标记样本的标记通过一定的概率传递给未标记样本，直到最终收敛。

谱聚类算法总结

谱聚类算法是一个使用起来简单，但是讲清楚却不是那么容易的算法，它需要你有一定的数学基础。如果你掌握了谱聚类，相信你会对矩阵分析，图论有更深入的理解。同时对降维里的主成分分析也会加深理解。

　  下面总结下谱聚类算法的优缺点。

　　谱聚类算法的主要优点有：

　　1）谱聚类只需要数据之间的相似度矩阵，因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到

　　2）由于使用了降维，因此在处理高维数据聚类时的复杂度比传统聚类算法好。

　　谱聚类算法的主要缺点有：

　　1）如果最终聚类的维度非常高，则由于降维的幅度不够，谱聚类的运行速度和最后的聚类效果均不好。

　　2) 聚类效果依赖于相似矩阵，不同的相似矩阵得到的最终聚类效果可能很不同。