数据分析与展示——Pandas数据特征分析
Pandas数据特征分析
数据的排序
将一组数据通过摘要(有损地提取数据特征的过程)的方式,可以获得基本统计(含排序)、分布/累计统计、数据特征(相关性、周期性等)、数据挖掘(形成知识)。
- .sort_index()方法在指定轴上根据索引进行排序,默认升序
- .sort_index(axis=0, ascending=True)
In [1]: import pandas as pd In [2]: import numpy as np In [3]: b = pd.DataFrame(np.arange(20).reshape(4,5), index=['c','a','d','b']) In [4]: b Out[4]: 0 1 2 3 4 c 0 1 2 3 4 a 5 6 7 8 9 d 10 11 12 13 14 b 15 16 17 18 19 In [5]: b.sort_index() Out[5]: 0 1 2 3 4 a 5 6 7 8 9 b 15 16 17 18 19 c 0 1 2 3 4 d 10 11 12 13 14 In [6]: b.sort_index(ascending=False) Out[6]: 0 1 2 3 4 d 10 11 12 13 14 c 0 1 2 3 4 b 15 16 17 18 19 a 5 6 7 8 9 In [7]: c = b.sort_index(axis=1, ascending=False) In [8]: c Out[8]: 4 3 2 1 0 c 4 3 2 1 0 a 9 8 7 6 5 d 14 13 12 11 10 b 19 18 17 16 15 In [9]: c = c.sort_index() In [10]: c Out[10]: 4 3 2 1 0 a 9 8 7 6 5 b 19 18 17 16 15 c 4 3 2 1 0 d 14 13 12 11 10
- .sort_values()方法在指定轴上根据数值进行排序,默认升序
Series.sort_values(axis=0, ascending=True) DataFrame.sort_values(by, axis=0, ascending=True) # by:axis轴上的某个索引或索引列表
In [11]: c = b.sort_values(2,ascending=False) In [12]: c Out[12]: 0 1 2 3 4 b 15 16 17 18 19 d 10 11 12 13 14 a 5 6 7 8 9 c 0 1 2 3 4 In [13]: c = c.sort_values('a',axis=1,ascending=False) In [14]: c Out[14]: 4 3 2 1 0 b 19 18 17 16 15 d 14 13 12 11 10 a 9 8 7 6 5 c 4 3 2 1 0
Nan统一放到排序末尾
In [15]: a = pd.DataFrame(np.arange(12).reshape(3,4), index=['a','b','c']) In [16]: a Out[16]: 0 1 2 3 a 0 1 2 3 b 4 5 6 7 c 8 9 10 11 In [17]: c = a + b In [18]: c Out[18]: 0 1 2 3 4 a 5.0 7.0 9.0 11.0 NaN b 19.0 21.0 23.0 25.0 NaN c 8.0 10.0 12.0 14.0 NaN d NaN NaN NaN NaN NaN In [19]: c.sort_values(2,ascending=False) Out[19]: 0 1 2 3 4 b 19.0 21.0 23.0 25.0 NaN c 8.0 10.0 12.0 14.0 NaN a 5.0 7.0 9.0 11.0 NaN d NaN NaN NaN NaN NaN In [20]: c.sort_values(2,ascending=True) Out[20]: 0 1 2 3 4 a 5.0 7.0 9.0 11.0 NaN c 8.0 10.0 12.0 14.0 NaN b 19.0 21.0 23.0 25.0 NaN d NaN NaN NaN NaN NaN
数据的基本统计分析
基本的统计分析函数
适用于Series和DataFrame类型
| 方法 | 说明 |
|---|---|
| .sum() | 计算数据的总和,按0轴计算,下同 |
| .count() | 非Nan值得数量 |
| .mean() .median() | 计算数据的算术平均值、算术中位数 |
| .var() .std() | 计算数据的方差、标准差 |
| .min() .max() | 计算数据的最小值、最大值 |
适用于Series类型
| 方法 | 说明 |
|---|---|
| .argmin() .argmax() | 计算数据最大值、最小值所在位置的索引位置(自动索引) |
| .idxmin() .idxmax() | 计算数据最大值、最小值所在位置的索引(自定义索引) |
适用于Series和DataFrame类型
| 方法 | 说明 |
|---|---|
| .describe() | 针对0轴(各列)的统计汇总 |
In [21]: a = pd.Series([9,8,7,6], index=['a','b','c','d']) In [22]: a Out[22]: a 9 b 8 c 7 d 6 dtype: int64 In [23]: a.describe() Out[23]: count 4.000000 mean 7.500000 std 1.290994 min 6.000000 25% 6.750000 50% 7.500000 75% 8.250000 max 9.000000 dtype: float64 In [24]: type(a.describe()) Out[24]: pandas.core.series.Series In [25]: a.describe()['count'] Out[25]: 4.0 In [26]: a.describe()['max'] Out[26]: 9.0 In [27]: b.describe() Out[27]: 0 1 2 3 4 count 4.000000 4.000000 4.000000 4.000000 4.000000 mean 7.500000 8.500000 9.500000 10.500000 11.500000 std 6.454972 6.454972 6.454972 6.454972 6.454972 min 0.000000 1.000000 2.000000 3.000000 4.000000 25% 3.750000 4.750000 5.750000 6.750000 7.750000 50% 7.500000 8.500000 9.500000 10.500000 11.500000 75% 11.250000 12.250000 13.250000 14.250000 15.250000 max 15.000000 16.000000 17.000000 18.000000 19.000000 In [28]: type(b.describe()) Out[28]: pandas.core.frame.DataFrame In [29]: In [30]: b.describe().ix['max'] __main__:1: DeprecationWarning: .ix is deprecated. Please use .loc for label based indexing or .iloc for positional indexing See the documentation here: http://pandas.pydata.org/pandas-docs/stable/indexing.html#ix-indexer-is-deprecated Out[30]: 0 15.0 1 16.0 2 17.0 3 18.0 4 19.0 Name: max, dtype: float64 In [31]: b.describe()[2] Out[31]: count 4.000000 mean 9.500000 std 6.454972 min 2.000000 25% 5.750000 50% 9.500000 75% 13.250000 max 17.000000 Name: 2, dtype: float64
数据的累计统计分析
累计统计分析函数
适用于Series和DataFrame类型,累计计算
| 方法 | 说明 |
|---|---|
| .cumsum() | 依次给出前1、2、… 、n个数的和 |
| .cumprod() | 依次给出前1、2、… 、n个数的积 |
| .cummax() | 依次给出前1、2、… 、n个数的最大值 |
| .cummin() | 依次给出前1、2、… 、n个数的最小值 |
In [32]: b.cumsum() Out[32]: 0 1 2 3 4 c 0 1 2 3 4 a 5 7 9 11 13 d 15 18 21 24 27 b 30 34 38 42 46 In [33]: b.cumprod() Out[33]: 0 1 2 3 4 c 0 1 2 3 4 a 0 6 14 24 36 d 0 66 168 312 504 b 0 1056 2856 5616 9576 In [34]: b.cummin() Out[34]: 0 1 2 3 4 c 0 1 2 3 4 a 0 1 2 3 4 d 0 1 2 3 4 b 0 1 2 3 4 In [35]: b.cummax() Out[35]: 0 1 2 3 4 c 0 1 2 3 4 a 5 6 7 8 9 d 10 11 12 13 14 b 15 16 17 18 19
适用于Series和DataFrame类型,滚动计算(窗口计算)
| 方法 | 说明 |
|---|---|
| .rolling(w).sum() | 依次计算相邻w个元素的和 |
| .rolling(w).mean() | 依次计算相邻w个元素的算术平均值 |
| .rolling(w).var() | 依次计算相邻w个元素的方差 |
| .rolling(w).std() | 依次计算相邻w个元素的标准差 |
| .rolling(w).min() .max() | 依次计算相邻w个元素的最小值和最大值 |
In [36]: b.rolling(2).sum() Out[36]: 0 1 2 3 4 c NaN NaN NaN NaN NaN a 5.0 7.0 9.0 11.0 13.0 d 15.0 17.0 19.0 21.0 23.0 b 25.0 27.0 29.0 31.0 33.0 In [37]: b.rolling(3).sum() Out[37]: 0 1 2 3 4 c NaN NaN NaN NaN NaN a NaN NaN NaN NaN NaN d 15.0 18.0 21.0 24.0 27.0 b 30.0 33.0 36.0 39.0 42.0
数据的相关分析
两个事物,表示为X和Y,如何判断它们之间的存在相关性?
相关性
- X增大,Y增大,两个变量正相关
- X增大,Y减小,两个变量负相关
- X增大,Y无视,两个变量不相关
协方差
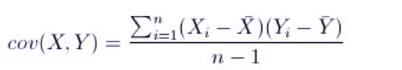
- 协方差>0, X和Y正相关
- 协方差<0, X和Y负相关
- 协方差=0, X和Y独立无关
Pearson相关系数
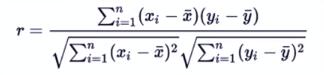
r取值范围[-1, 1]
- 0.8 - 1.0 极强相关
- 0.6 - 0.8 强相关
- 0.4 - 0.6 中等程度相关
- 0.2 - 0.4 弱相关
- 0.0 - 0.2 极弱相关或无相关
适用于Series和DataFrame类型
| 方法 | 说明 |
|---|---|
| .cov() | 计算协方差矩阵 |
| .corr() | 计算相关系数矩阵,Pearson、Spearman、Kendall等系数 |
In [38]: import pandas as pd In [39]: hprice = pd.Series([3.04, 22.93, 12.75, 22.6, 12.33], index=['2008', '2009', '2010', '2011', '2012']) In [40]: m2 = pd.Series([8.18, 18.38, 9.13, 7.82, 6.69], index=['2008', '2009', '2010','2011', '2012']) In [41]: hprice.corr(m2) Out[41]: 0.5239439145220387


 浙公网安备 33010602011771号
浙公网安备 33010602011771号