BUAA OO 第一单元作业总结

BUAA OO 第一单元作业总结

一、题目简介

​ 第一次作业为最多含有一层深度括号的单变量表达式恒等变形展开所有括号，包含加、减、乘和乘方运算。

​ 第二次作业在第一次作业基础上增加了三角函数、求和函数以及自定义函数调用。

​ 第三次作业增加了多层嵌套的要求，包括括号的嵌套以及函数调用的嵌套。

二、程序结构分析

总体思路为将表达式递归下降解析为后缀表达式，再根据后缀表达式进行运算。

（一）类图及分析

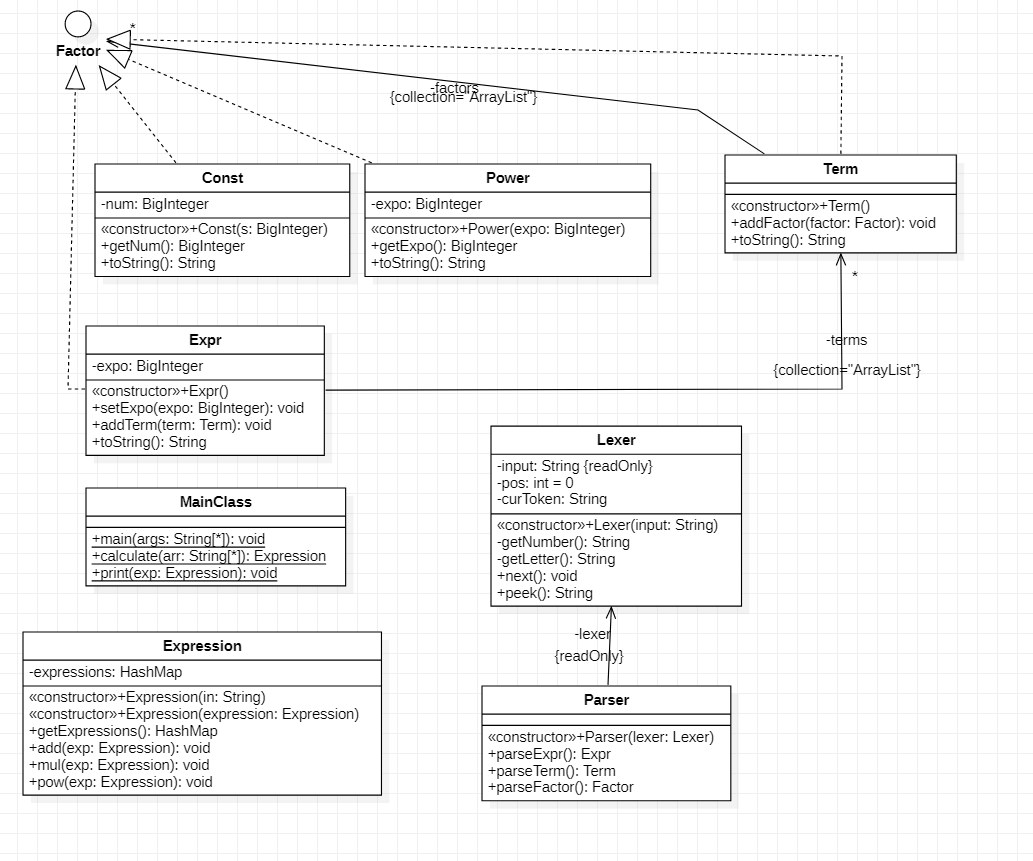
1. 第一次作业

• MainClass

  负责读入数据，对分析后的表达式进行计算，最后进行输出

• Parser

  语法分析器，以运算符为分割解析表达式

• Lexer

  词法分析器，分析输入表达式中变量、常数、运算符、括号等等

• Factor

  底层接口，为表达式中因子

  • Const

    常数因子

  • Power

    幂函数因子

  • Term

    项，由因子构成

  • Expr

    表达式，由项构成，同时也可以为因子

• Expression

  计算时表达式存储类，用一个HashMap来存储

优点：

1. 运用递归下降思想，在此次作业中定下了适用三次作业的架构，之后不用重构

2. 将表达式解析和运算分离开来，便于分开调试

缺点：

1. 将解析和运算分离，可以将运算整合在各个类里，代码冗余

2.第二次作业

• MainClass

  对分析后的表达式进行计算

• Input

  负责读入数据，对表达式进行预处理

• Output

  负责最后的输出格式整理

• Parser

  语法分析器，以运算符为分割解析表达式

• Lexer

  词法分析器，分析输入表达式中变量、常数、运算符、括号等等

• Factor

  底层接口，为表达式中因子

  • Const

    常数因子

  • Power

    幂函数因子

  • Sin、Cos

    三角函数因子

  • Sum

    求和函数，直接返回一个处理后的表达式

  • CustomFunc

    自定义函数存储，用来进行函数调用

  • Term

    项，由因子构成

  • Expr

    表达式，由项构成，同时也可以为因子

• Expression

  计算时表达式存储类，用一个HashMap来存储

优点：

1. 用HashMap中嵌套HashMap存储表达式，减少了存储和输出时的各种错误

缺点：

1. 将解析和运算分离，代码冗余

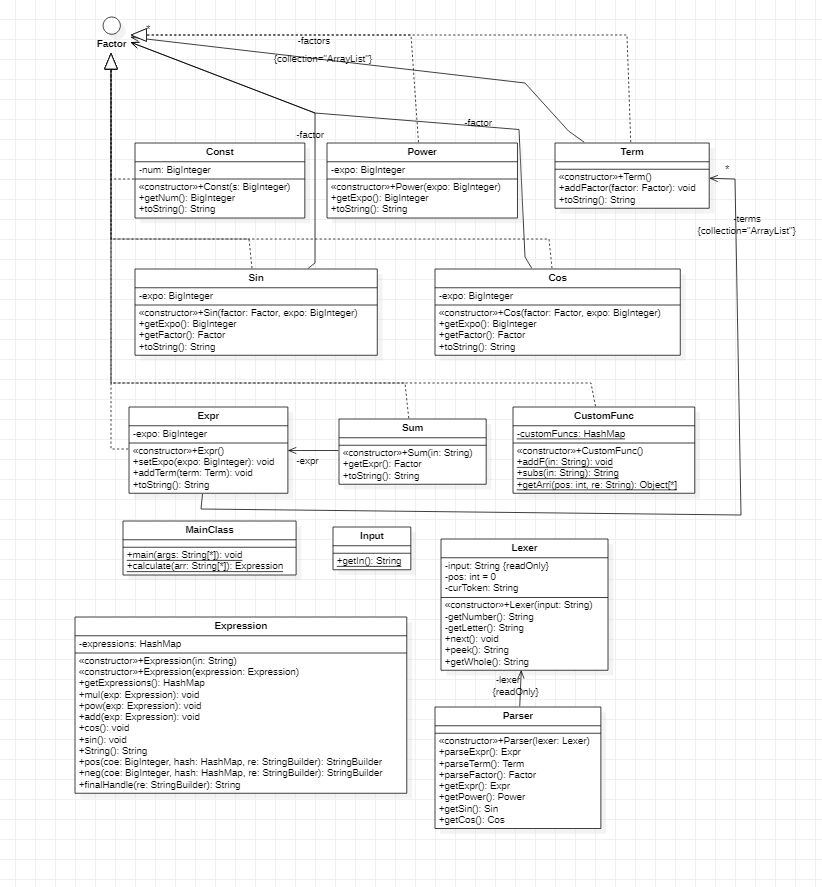
3.第三次作业

• MainClass

  对分析后的表达式进行计算

• Input

  负责读入数据，对表达式进行预处理

• Parser

  语法分析器，以运算符为分割解析表达式

• Lexer

  词法分析器，分析输入表达式中变量、常数、运算符、括号等等

• Factor

  底层接口，为表达式中因子

  • Const

    常数因子

  • Power

    幂函数因子

  • Sin、Cos

    三角函数因子

  • Sum

    求和函数，直接返回一个处理后的表达式

  • CustomFunc

    自定义函数存储，用来进行函数调用

  • Term

    项，由因子构成

  • Expr

    表达式，由项构成，同时也可以为因子

• Expression

  计算时表达式存储类，用一个HashMap来存储。

  整合toString方法。

优点：

1. 沿用前两次的递归下降架构，便于进行嵌套处理

缺点：

1. 同前两次作业，将解析和运算分离，代码冗余

（二）度量分析

1.第一次作业

Class	OCavg	OCmax	WMC
Const	1	1	3
Expr	1.75	4	7
Expression	2.83	5	17
Lexer	2.2	6	11
MainClass	7.33	14	22
Parser	3.5	9	14
Power	1.33	2	4
Term	1.67	3	5
Total			83
Average	2.677419355	5.5	10.375

第一次的代码复杂度总体还可以，除了MainClass类承担了全部运算导致复杂度上升，Parser类承担了对表达式的语法解析，需要大量使用，复杂度较高，Expression类用来存储表达式导致复杂度较高

2.第二次作业

Class	OCavg	OCmax	WMC
Const	1	1	3
Cos	1.25	2	5
CustomFunc	1.33	2	4
CustomFunc.F	1	1	1
Expr	1.75	4	7
Expression	3.25	5	26
Input	2	2	2
Lexer	3	8	18
MainClass	6	11	12
Output	6.25	9	25
Parser	3.5	8	28
Power	1.33	2	4
Sin	1.25	2	5
Sum	2	4	6
Term	1.67	3	5
Total			151
Average	2.649122807	4.266666667	10.06666667

类似于第一次作业，复杂度较高的类为MainClass、Output、Expression、Parser，在此次作业中，将MainClass中输出部分拆分成Output类，输出中条件判断较多导致Output类复杂度较高

3.第三次作业

Class	OCavg	OCmax	WMC
Const	1	1	3
Cos	1.25	2	5
CustomFunc	3	4	12
CustomFunc.F	1	1	1
Expr	1.75	4	7
Expression	4.25	9	51
Input	2	2	2
Lexer	3	8	18
MainClass	6	11	12
Parser	3.5	8	28
Power	1.33	2	4
Sin	1.25	2	5
Sum	2	4	6
Term	1.67	3	5
Total			159
Average	2.74137931	4.357142857	11.35714286

类似于前两次作业，复杂度较高的类为MainClass、Expression、Parser、Lexer、CustomFunc，其中Expression类整合入了toString方法，相当于将第二次作业中的输出整合到了类中，导致复杂度上升，Lexer类中由于因子种类增多且增加嵌套要求，导致取各个因子时的条件判断增多，复杂度升高，CustomFunc类对于函数调用时的替换对逗号的分隔较为复杂，导致复杂度高

（三）方法圈复杂度分析

1.第一次作业

Method	CogC	ev(G)	iv(G)	v(G)
Const.Const(BigInteger)	0	1	1	1
Const.getNum()	0	1	1	1
Const.toString()	0	1	1	1
Expr.Expr()	0	1	1	1
Expr.addTerm(Term)	0	1	1	1
Expr.setExpo(BigInteger)	0	1	1	1
Expr.toString()	4	1	4	4
Expression.Expression(Expression)	0	1	1	1
Expression.Expression(String)	5	1	3	3
Expression.add(Expression)	8	1	4	4
Expression.getExpressions()	0	1	1	1
Expression.mul(Expression)	12	1	5	5
Expression.pow(Expression)	4	1	3	3
Lexer.Lexer(String)	0	1	1	1
Lexer.getLetter()	0	1	1	1
Lexer.getNumber()	2	1	3	3
Lexer.next()	5	2	5	6
Lexer.peek()	0	1	1	1
MainClass.calculate(List)	7	1	3	6
MainClass.main(String[])	0	1	1	1
MainClass.print(Expression)	36	1	13	14
Parser.Parser(Lexer)	0	1	1	1
Parser.parseExpr()	1	1	2	2
Parser.parseFactor()	21	5	9	9
Parser.parseTerm()	1	1	2	2
Power.Power(BigInteger)	0	1	1	1
Power.getExpo()	0	1	1	1
Power.toString()	2	1	2	2
Term.Term()	0	1	1	1
Term.addFactor(Factor)	0	1	1	1
Term.toString()	3	1	3	3
Total	111	36	78	83
Average	3.580645161	1.161290323	2.516129032	2.677419355

由上表可以看出，方法整体复杂度与类的耦合度都较低，但是存在个别方法的复杂度过高。Expression类的add()mul()两个运算方法因为考虑到存储关系的原因导致复杂度较高；MainClass类中的print()方法因为涉及到优化输出、简化等，判断条件嵌套较多，且if-else分支较多，不便于维护；Parser类中的parseFactor()因为需要解析的因子类型较多，所以判断条件if-else分支较多，且较难减弱。

2.第二次作业

Method	CogC	ev(G)	iv(G)	v(G)
Const.Const(BigInteger)	0	1	1	1
Const.getNum()	0	1	1	1
Const.toString()	0	1	1	1
Cos.Cos(Factor, BigInteger)	0	1	1	1
Cos.getExpo()	0	1	1	1
Cos.getFactor()	0	1	1	1
Cos.toString()	1	1	2	2
CustomFunc.CustomFunc()	0	1	1	1
CustomFunc.F.F(String)	0	1	1	1
CustomFunc.addF(String)	0	1	1	1
CustomFunc.subs(String)	1	1	2	2
Expr.Expr()	0	1	1	1
Expr.addTerm(Term)	0	1	1	1
Expr.setExpo(BigInteger)	0	1	1	1
Expr.toString()	4	1	4	4
Expression.Expression(Expression)	0	1	1	1
Expression.Expression(String)	5	1	3	3
Expression.add(Expression)	8	1	4	4
Expression.cos()	9	1	5	5
Expression.getExpressions()	0	1	1	1
Expression.mul(Expression)	6	1	4	4
Expression.pow(Expression)	4	1	3	3
Expression.sin()	9	1	5	5
Input.getIn()	1	1	2	2
Lexer.Lexer(String)	0	1	1	1
Lexer.getLetter()	2	1	3	3
Lexer.getNumber()	2	1	3	3
Lexer.getWhole()	5	1	4	4
Lexer.next()	8	2	7	8
Lexer.peek()	0	1	1	1
MainClass.calculate(List)	11	1	4	9
MainClass.main(String[])	0	1	1	1
Output.finalHandle(StringBuilder)	2	1	2	3
Output.neg(BigInteger, HashMap<String, BigInteger>, StringBuilder)	16	1	9	9
Output.pos(BigInteger, HashMap<String, BigInteger>, StringBuilder)	16	1	9	9
Output.string(Expression)	4	1	4	4
Parser.Parser(Lexer)	0	1	1	1
Parser.getCos()	6	1	4	4
Parser.getExpr()	7	1	4	4
Parser.getPower()	4	2	3	3
Parser.getSin()	6	1	4	4
Parser.parseExpr()	1	1	2	2
Parser.parseFactor()	9	8	8	8
Parser.parseTerm()	1	1	2	2
Power.Power(BigInteger)	0	1	1	1
Power.getExpo()	0	1	1	1
Power.toString()	2	1	2	2
Sin.Sin(Factor, BigInteger)	0	1	1	1
Sin.getExpo()	0	1	1	1
Sin.getFactor()	0	1	1	1
Sin.toString()	1	1	2	2
Sum.Sum(String)	7	1	4	4
Sum.getExpr()	0	1	1	1
Sum.toString()	0	1	1	1
Term.Term()	0	1	1	1
Term.addFactor(Factor)	0	1	1	1
Term.toString()	3	1	3	3
Total	161	66	144	151
Average	2.824561404	1.157894737	2.526315789	2.649122807

同第一次，整体复杂度与类的耦合度都较低，但是存在个别方法的复杂度过高。Expression类的mul()两个运算方法因为存储形式变化，复杂度有所降低，增加sin()cos()方法，涉及toString方法条件较多；MainClass类中的calculate方法包含所有计算，有较多判断分支；Output类中对正负系数的分析输出因需考虑优化导致判断条件分支及嵌套多；Parser类中的方法复杂度分摊到各个分方法中，但仍因为需要解析的因子类型较多且解析较为复杂，方法圈复杂度仍较高。

3.第三次作业

Method	CogC	ev(G)	iv(G)	v(G)
Const.Const(BigInteger)	0	1	1	1
Const.getNum()	0	1	1	1
Const.toString()	0	1	1	1
Cos.Cos(Factor, BigInteger)	0	1	1	1
Cos.getExpo()	0	1	1	1
Cos.getFactor()	0	1	1	1
Cos.toString()	1	1	2	2
CustomFunc.CustomFunc()	0	1	1	1
CustomFunc.F.F(String)	0	1	1	1
CustomFunc.addF(String)	0	1	1	1
CustomFunc.getArri(int, String)	6	1	6	6
CustomFunc.subs(String)	7	1	6	8
Expr.Expr()	0	1	1	1
Expr.addTerm(Term)	0	1	1	1
Expr.setExpo(BigInteger)	0	1	1	1
Expr.toString()	4	1	4	4
Expression.Expression(Expression)	0	1	1	1
Expression.Expression(String)	5	1	3	3
Expression.add(Expression)	8	1	4	4
Expression.cos()	5	1	5	5
Expression.finalHandle(StringBuilder)	2	1	2	3
Expression.getExpressions()	0	1	1	1
Expression.mul(Expression)	6	1	4	4
Expression.neg(BigInteger, HashMap<String, BigInteger>, StringBuilder)	16	1	9	9
Expression.pos(BigInteger, HashMap<String, BigInteger>, StringBuilder)	16	1	9	9
Expression.pow(Expression)	4	1	3	3
Expression.sin()	5	1	5	5
Expression.string()	4	1	4	4
Input.getIn()	1	1	2	2
Lexer.Lexer(String)	0	1	1	1
Lexer.getLetter()	2	1	3	3
Lexer.getNumber()	2	1	3	3
Lexer.getWhole()	5	1	4	4
Lexer.next()	8	2	7	8
Lexer.peek()	0	1	1	1
MainClass.calculate(List)	11	1	4	9
MainClass.main(String[])	0	1	1	1
Parser.Parser(Lexer)	0	1	1	1
Parser.getCos()	6	1	4	4
Parser.getExpr()	7	1	4	4
Parser.getPower()	4	2	3	3
Parser.getSin()	6	1	4	4
Parser.parseExpr()	1	1	2	2
Parser.parseFactor()	9	8	8	8
Parser.parseTerm()	1	1	2	2
Power.Power(BigInteger)	0	1	1	1
Power.getExpo()	0	1	1	1
Power.toString()	2	1	2	2
Sin.Sin(Factor, BigInteger)	0	1	1	1
Sin.getExpo()	0	1	1	1
Sin.getFactor()	0	1	1	1
Sin.toString()	1	1	2	2
Sum.Sum(String)	7	1	4	4
Sum.getExpr()	0	1	1	1
Sum.toString()	0	1	1	1
Term.Term()	0	1	1	1
Term.addFactor(Factor)	0	1	1	1
Term.toString()	3	1	3	3
Total	165	67	154	163
Average	2.844827586	1.155172414	2.655172414	2.810344828

同前一次，整体复杂度与类的耦合度都较低，但是存在个别方法的复杂度过高。Expression类中对正负系数的分析输出因需考虑优化导致判断条件分支及嵌套多；CustomFunc类中的取实参以及替换涉及到括号匹配导致方法较长且循环次数较多。

三、Bug分析

（一）第一次作业

第一次作业中在测试中出现的bug主要为对大数的分析以及对负号的处理，最后通过BigInteger和将负号替换为+-进行解析。

（二）第二次作业

第二次作业出现的bug为在求和函数里忽略了对i的两个边界的符号解析，在强测中错了两个点，在互测中因为没有自定义函数和求和函数所以没被找出bug。

（三）第三次作业

第三次作业出现的bug为对sin(0)的错误化简，将其化为1，导致在强测和互测中收到围殴。

四、Hack策略

在此单元的互测中，并没有很仔细对其他人的程序进行测试，只是将自己在测试时遇到的错误样例以及自己认为易错的点提交，导致互测中并没有怎么hack别人。

五、架构设计体验

在第一单元，在第一次作业中，对如何完成作业迟迟没有想法，直到受到训练的启发，在训练的基础上对表达式进行解析，完成了对表达式的递归下降解析，之后在第二次第三次作业中体现了这个架构的成功性，在之后的作业中不用进行重构就可以较好的完成作业，一个好的架构对完成任务是事半功倍的。

六、心得体会

因为在假期较好的完成了pre2、pre3的作业，在对java基础语法方面有了一定的了解，对面向对象思想有了一定的了解和应用，在经过了第一单元的作业后，也是明白了面向对象课程组为我们设置预习作业的良苦用心。同时也是首次经历课程中设置的这类研讨课，给我们提供了交流平台，对完成作业的优秀方案也能有效促进对课下作业的完成。

七、对课程的想法

据助教和往届学长透露的消息，下一单元设计线程的设计，但在即将开始的两三天前仍不知道线程该如何使用、设计等等，我觉得这是课程组可以提供部分资料供我们提前学习，避免因接触全新的东西导致每单元的第一次作业给人造成较大困扰。