2. 二叉查找树
一、二叉查找树是二叉树在查找领域的扩展,它既具有二分查找的高效性,又具有链表插入的灵活性
- 二分查找的高效性:每迭代一次,查找的范围就缩小一半。对于二叉查找树来说,每次查找的范围减少一棵子树(理想的情况是少一半结点)。
- 链式插入的灵活性:二叉查找树是链式结构,故插入结点不需要移动大段的内存数据,具备链表插入与删除的O(1)时间效率。
注:如下图所示的二叉查找树,每次迭代后,查找的范围只减少一个结点,查找的时间效率为O(n)。而二分查找的时间效率为O(logn),所以,二叉查找树的时间效率视具体树形而定,既可能为O(logn),也可能为O(n)。

图 1
图1展现了二叉查找树退化成链表这一问题,所以为了保持二叉查找树的高效性,将引出带有平衡条件的二叉树——平衡二叉树。
二、查找操作
1. 递归查找
BinaryTreeNode* find(BinaryTreeNode *pRoot, int x)
{
if(pRoot == nullptr)
return nullptr;
if(pRoot->value == x)
return pRoot;
else if(pRoot->value > x)
return find(pRoot->lChild, x);
else
return find(pRoot->rChild, x);
}
2. 非递归查找
BinaryTreeNode* find(BinaryTreeNode *pRoot, int x)
{
if(pRoot == nullptr)
return nullptr;
while(pRoot != nullptr && pRoot->value != x) {
if(pRoot->value > x)
pRoot = pRoot->lChild;
if(pRoot->value < x)
pRoot = pRoot->rChild;
}
return pRoot;
}
三、插入操作
1. 不含重复结点
BinaryTreeNode* insert(BinaryTreeNode *pRoot, int x)
{
if(pRoot == nullptr) {
pRoot = new BinaryTreeNode;
pRoot->value = x;
pRoot->lChild = nullptr;
pRoot->rChild = nullptr;
}
else {
if(pRoot->value > x)
pRoot->lChild = insert(pRoot->lChild, x);
if(pRoot->value < x)
pRoot->rChild = insert(pRoot->rChild, x);
// 如果要插入的结点已存在,则直接返回该已存在的结点
}
// 每次递归后就要返回当前的root值,以备上一层使用,最后返回整棵树的根结点
return pRoot;
}
分析:该代码存在纰漏,当传入的是一个空树时,该段代码并不会完成插入操作。究其原因,当我们往一个空链表插入一个结点时,新插入的结点就是链表的头指针,由于此时会改动头指针,因此必须把pRoot参数设为指向指针的指针,否则出了该函数pRoot仍然是一个空指针。总而言之,对于凡是涉及改动头指针的函数,传入的均应为指向头指针的指针。
BinaryTreeNode* insert(BinaryTreeNode **pRoot, int x) // pRoot为指向指针的指针
{
if(*pRoot == nullptr) {
*pRoot = new BinaryTreeNode;
(*pRoot)->value = x;
(*pRoot)->lChild = nullptr;
(*pRoot)->rChild = nullptr;
}
else {
if((*pRoot)->value > x)
(*pRoot)->lChild = insert(&((*pRoot)->lChild), x);
if((*pRoot)->value < x)
(*pRoot)->rChild = insert(&((*pRoot)->rChild), x);
}
return *pRoot;
}
2. 含重复的结点
若二叉查找树中含有重复的元素,则可以通过在结点结构体中保留一个辅助变量以指示发生的频率来处理重复的元素。
struct BinaryTreeNode {
int value;
unsigned int occur;
BinaryTreeNode *lChild;
BinaryTreeNode *rChild;
};
BinaryTreeNode* insert(BinaryTreeNode **pRoot, int x) // pRoot为指向指针的指针
{
if(*pRoot == nullptr) {
*pRoot = new BinaryTreeNode;
(*pRoot)->value = x;
(*pRoot)->occur = 1;
(*pRoot)->lChild = nullptr;
(*pRoot)->rChild = nullptr;
}
else {
if((*pRoot)->value > x)
(*pRoot)->lChild = insert(&((*pRoot)->lChild), x);
if((*pRoot)->value < x)
(*pRoot)->rChild = insert(&((*pRoot)->rChild), x);
if((*pRoot)->value == x)
(*pRoot)->occur++;
}
return *pRoot;
}
四、删除操作
BinaryTreeNode* DeleteNode(BinaryTreeNode *pRoot, int x)
{
if(pRoot == nullptr)
return nullptr;
if(pRoot->value > x)
pRoot->lChild = DeleteNode(pRoot->lChild, x);
if(pRoot->value < x)
pRoot->rChild = DeleteNode(pRoot->rChild, x);
if(pRoot->value == x) {
// 被删除的结点具有两个孩子
if(pRoot->lChild && pRoot->rChild) {
BinaryTreeNode *temp = findMin(pRoot->rChild);
pRoot->value = temp->value;
pRoot->lChild = DeleteNode(pRoot->rChild, x);
}
// 被删除的结点有零个或一个孩子
else {
BinaryTreeNode *pNode = pRoot;
if(pRoot->lChild == nullptr)
pRoot = pRoot->rChild;
else if(pRoot->rChild == nullptr)
pRoot = pRoot->lChild;
delete pNode;
}
}
return pRoot;
}
分析:删除操作比较复杂,需分情况进行讨论。如果结点没有孩子,则可直接删除;如果结点有一个孩子,则需调整其父结点的指针绕过该结点,然后再删除该结点;如果结点有两个孩子,一般的策略是用其右子树的最小的数据代替该结点的数据并递归地删除那个结点。
【摘抄】
假设p是要删除的结点,则分以下三种情况:
(1)p是叶子结点
若p是父母的左右孩子,设置p.parent结点的left/right为空,即删除p结点。
(2)p是1度结点
删除p结点并用p的孩子顶替作为其父母孩子,分以下情况:
①若p是父母的左孩子,且p只有左孩子,则设置p.parent.left指向p的左孩子,包含p是叶子。
②若p是父母的有孩子,且p只有右孩子,则设置p.parent.right指向p的右孩子,包含p是叶子。
(3)p是2度结点
为了减少对二叉查找树形态的影响,不直接删除一个2度结点p,而是先用p在中序次序下的后继结点q的值代替p结点值,再删除那个后继结点q。这样便将删除2度结点问题转化为删除1度结点或叶子结点。因为,q是p的右子树在中序次序下的第一个访问结点,若p的右孩子为叶子结点,则q是p的右孩子;否则q是p的右孩子的最左边的一个子孙结点,q的度为0或1。
五、完整代码
#include <iostream>
#include <stack>
#include <queue>
using namespace std;
struct BinaryTreeNode {
int value;
BinaryTreeNode *lChild;
BinaryTreeNode *rChild;
};
/* 建立一棵二叉查找树 */
BinaryTreeNode* create(int InOrder[], int PostOrder[], int n)
{
if(InOrder == nullptr || PostOrder == nullptr || n == 0)
return nullptr;
BinaryTreeNode *pRoot = new BinaryTreeNode;
pRoot->value = PostOrder[n-1];
int lChildNum = 0, rChildNum = 0;
for(; lChildNum < n; ++lChildNum) {
if(InOrder[lChildNum] == pRoot->value)
break;
}
rChildNum = n - lChildNum - 1;
pRoot->lChild = create(InOrder, PostOrder, lChildNum);
pRoot->rChild = create(InOrder + lChildNum + 1, PostOrder + lChildNum, rChildNum);
return pRoot;
}
/* 中序遍历二叉查找树 */
void InOrderTraverse(BinaryTreeNode *pRoot)
{
if(pRoot) {
InOrderTraverse(pRoot->lChild);
cout << pRoot->value;
InOrderTraverse(pRoot->rChild);
}
}
/* 查询某个结点 */
BinaryTreeNode* find(BinaryTreeNode *pRoot, int x)
{
if(pRoot == nullptr)
return nullptr;
while(pRoot != nullptr && pRoot->value != x) {
if(pRoot->value > x)
pRoot = pRoot->lChild;
if(pRoot->value < x)
pRoot = pRoot->rChild;
}
return pRoot;
}
/* 查找最小元 */
BinaryTreeNode* findMin(BinaryTreeNode *pRoot)
{
if(pRoot == nullptr)
return nullptr;
while(pRoot->lChild != nullptr) {
pRoot = pRoot->lChild;
}
return pRoot;
}
/* 查找最大元 */
BinaryTreeNode* findMax(BinaryTreeNode *pRoot)
{
if(pRoot == nullptr)
return nullptr;
while(pRoot->rChild != nullptr) {
pRoot = pRoot->rChild;
}
return pRoot;
}
/* 插入操作 */
BinaryTreeNode* insert(BinaryTreeNode **pRoot, int x) // pRoot为指向指针的指针
{
if(*pRoot == nullptr) {
*pRoot = new BinaryTreeNode;
(*pRoot)->value = x;
(*pRoot)->lChild = nullptr;
(*pRoot)->rChild = nullptr;
}
else {
if((*pRoot)->value > x)
(*pRoot)->lChild = insert(&((*pRoot)->lChild), x);
if((*pRoot)->value < x)
(*pRoot)->rChild = insert(&((*pRoot)->rChild), x);
}
return *pRoot;
}
/* 删除操作 */
BinaryTreeNode* DeleteNode(BinaryTreeNode *pRoot, int x)
{
if(pRoot == nullptr)
return nullptr;
if(pRoot->value > x)
pRoot->lChild = DeleteNode(pRoot->lChild, x);
if(pRoot->value < x)
pRoot->rChild = DeleteNode(pRoot->rChild, x);
if(pRoot->value == x) {
// 被删除的结点具有两个孩子
if(pRoot->lChild && pRoot->rChild) {
BinaryTreeNode *temp = findMin(pRoot->rChild);
pRoot->value = temp->value;
pRoot->lChild = DeleteNode(pRoot->rChild, x);
}
// 被删除的结点有零个或一个孩子
else {
BinaryTreeNode *pNode = pRoot;
if(pRoot->lChild == nullptr)
pRoot = pRoot->rChild;
else if(pRoot->rChild == nullptr)
pRoot = pRoot->lChild;
delete pNode;
}
}
return pRoot;
}
int main()
{
int InOrd[7] = {1, 2, 3, 4, 6, 8};
int PostOrd[7] = {1, 3, 4, 2, 8, 6};
BinaryTreeNode *pTree = create(InOrd, PostOrd, 6);
cout << "提示:二叉查找树创建完毕!" << endl;
cout << "提示:中序遍历二叉查找树..." << endl;
InOrderTraverse(pTree);
cout << endl;
BinaryTreeNode *pNode = nullptr;
// 查找元素值为4的结点
pNode = find(pTree, 4);
if(pNode == nullptr)
cout << "提示:要找的结点不存在" << endl;
else
cout << "提示:要找的结点已找到" << endl;
// 插入元素值为7的结点
pNode = insert(&pTree, 7);
cout << "提示:要插入的结点已插入" << endl;
cout << "提示:中序遍历二叉树..." << endl;
InOrderTraverse(pTree);
cout << endl;
// 删除元素值为3的结点
pNode = DeleteNode(pTree, 3);
cout << "提示:要删除的结点已删除" << endl;
cout << "提示:中序遍历二叉树..." << endl;
InOrderTraverse(pTree);
cout << endl;
return 0;
}
测试结果:
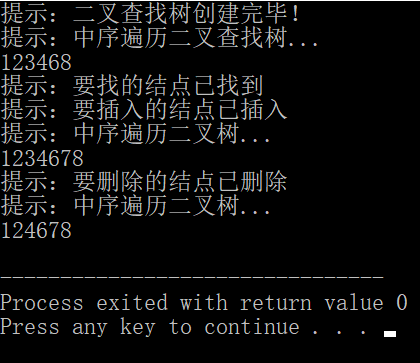
【建立的二叉查找树】
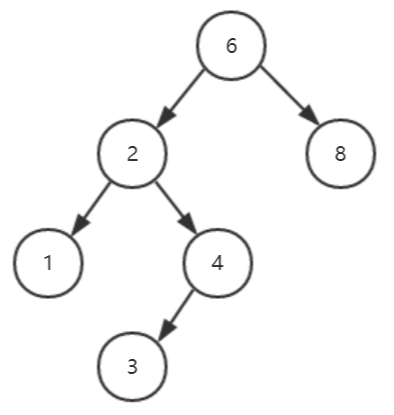
【插入结点7后的二叉查找树】
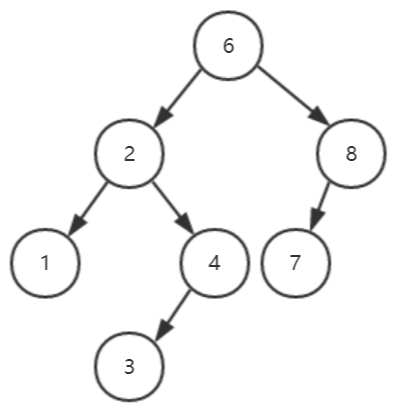
【删除结点3后的二叉查找树】



 浙公网安备 33010602011771号
浙公网安备 33010602011771号