强化学习 - Agent、状态、动作、奖励、Markov 决策过程

强化学习 - 基本概念

智能体与状态、动作

下面引入一个经典的网格世界的例子：

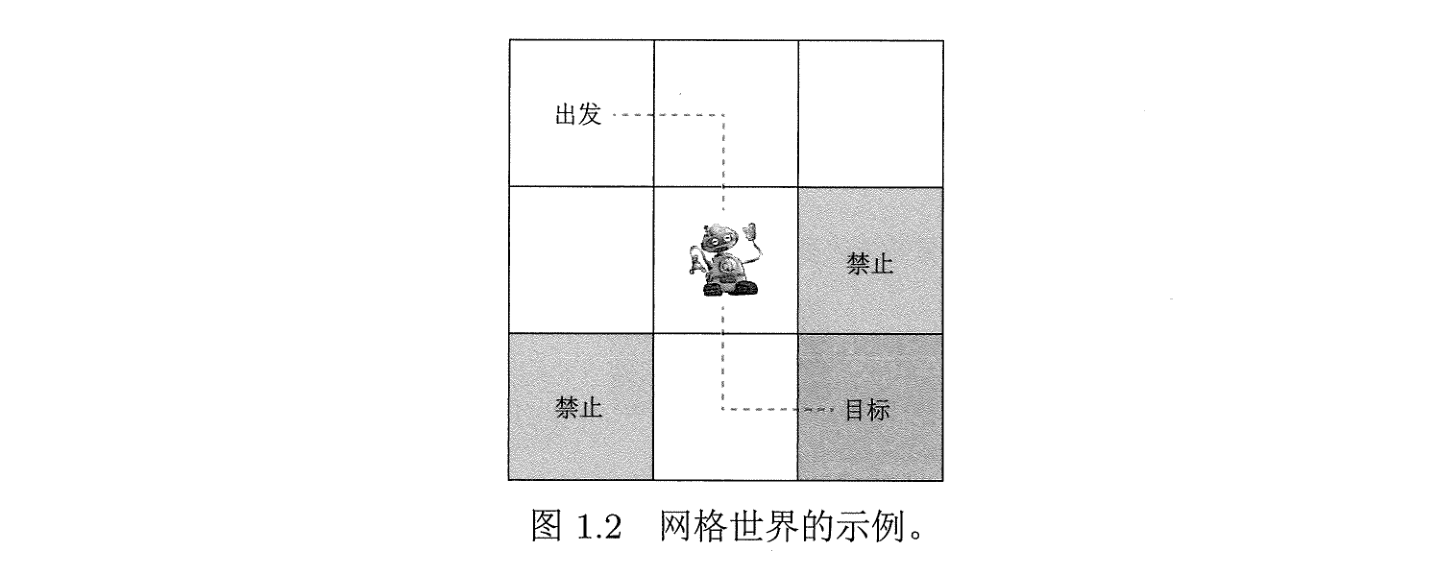
一般而言，强化学习研究的对象是智能体 (agent)，它在环境当中进行行动，并得到外界的反馈.

我们有第一个概念为状态 (state) ，它表示智能体与环境的相对状况，在网格世界当中，有九个格子，我们可以给出 9 个状态 \(s_{1},\cdots,s_{9}\) ，在此基础上，状态的全体构成一个集合：

\[\mathcal{S} = \left\lbrace s_{1},s_{2},\cdots, s_{9} \right\rbrace \]

这个集合称为状态空间，注意这个空间单纯就只是集合，没有加入别的运算规则.

然后，agent 在这个网格世界当中可以有很多动作 (action)，例如上下左右移动，也可以待在原地不动，共有五个动作分别为上、右、下、左、不动： \(a_{1},\cdots,a_{5}\) ，它们的全体构成集合：

\[\mathcal{A} = \left\lbrace a_{1},\cdots, a_{5} \right\rbrace \]

这个集合称为动作空间.

不同的状态可能有不同的动作空间，例如第一个格子就无法往上或者往左，那么此时就用 \(\mathcal{A}(s_{1})\) 来表示对应的动作空间.

状态转移 (state transition)

确定性状态转移

一般而言，采取一个动作之后，就会发生状态的转移，例如从 \(s_{1}\) 往右，就会得到 \(s_{2}\) ，那么符号表示为 \(s_{1}\xrightarrow{a_{2}}s_{2}\) .

对于特殊区域，我们下面分为两种情况讨论：

• 如果 \(s_{1}\) 往左，那么将会跳出状态空间，这显然是禁止的，因此我们设定经过 \(a_{4}\) 动作后有 \(s_{1}\xrightarrow{a_{4}}s_{1}\) .
• 对于网格世界的禁止区域，有两种方式：
  • 第一种：完全禁止进入，此时和刚刚的跳出状态空间的处理方法一致；
  • 第二种：允许进入，但施加惩罚，这个方法有的时候能让 agent 给出一些出人意料的方案.

不确定性状态转移

很多时候，agent 选择一个动作之后，它的状态转移是随机的，假设一个这样的场景：agent 投骰子来决定自己得到的分数，那么此时的分数状态就是随机的，为了描述这种场景，就考虑使用条件概率来描述：假设点数为多少就是多少分，\(s_{i}\) 表示有 \(i\) 分的状态，\(a_{1}\) 表示投骰子，那么

\[p(s_{1}\mid s_{0}, a_{1}) = \frac{1}{6}, \cdots , p(s_{6}\mid s_{0}, a_{1}) = \frac{1}{6} \]

在网格世界的例子当中，我们只考虑确定性的状态转移.

策略 (Policy)

策略可以理解为一种行动可能性，可以通过如下所示的轨迹来说明网格世界里面的策略.

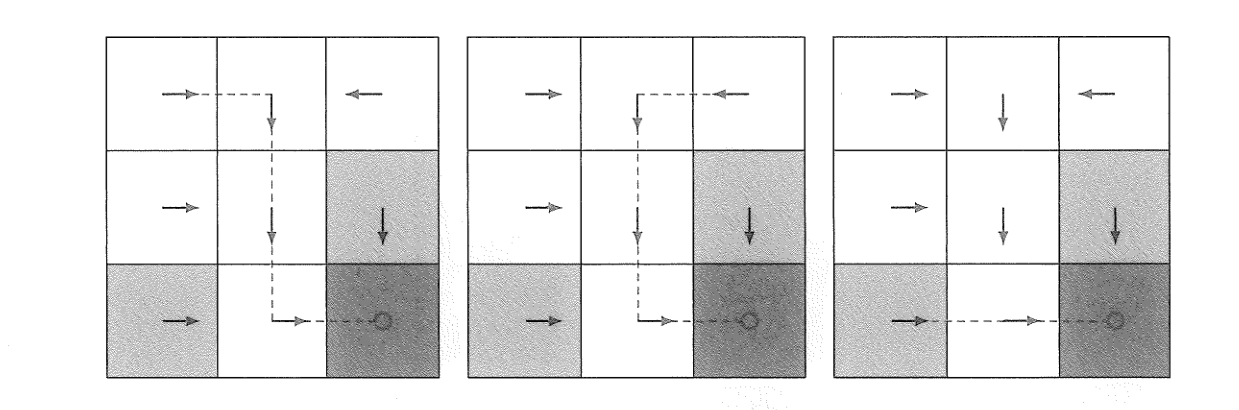
数学上，策略通过一种概率函数 \(\pi\) 来说明，用 \(\pi(a\mid s)\) 表示在状态 \(s\) 下，采用动作 \(a\) 的概率是多少.

\(\pi\) 也分为确定性和随机性策略，确定性就是在 \(s\) 固定时，\(\pi\) 会在某个动作 \(a\) 下输出概率 \(1\) ，随机性策略可以参考下图：

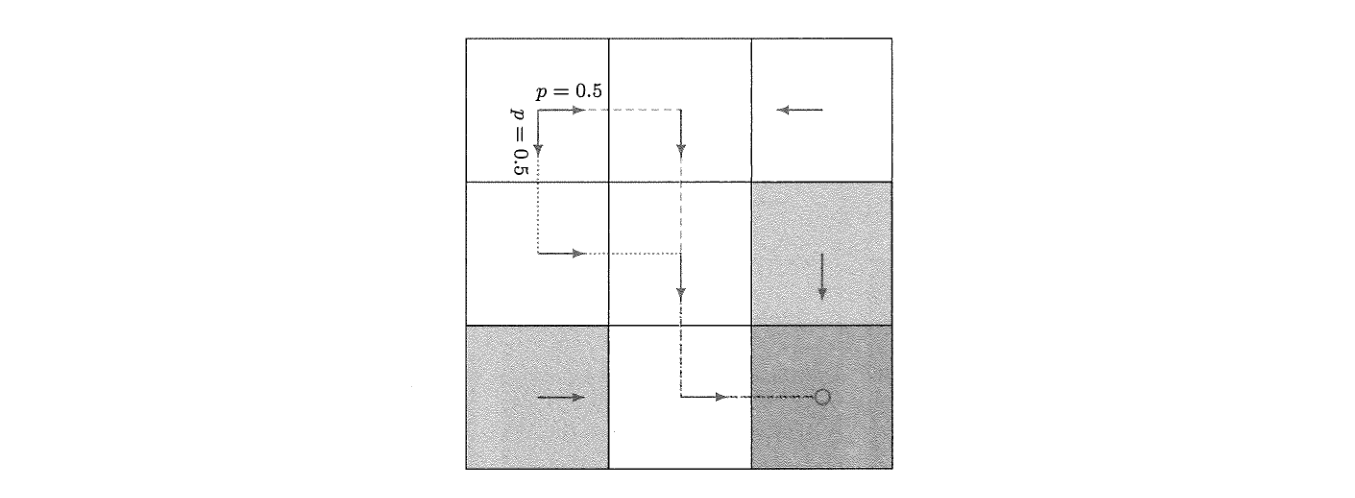
这个时候就可以说 \(\pi(a_{2}\mid s_{1}) = 0.5\) ，\(\pi(a_{3}\mid s_{1})=0.5\) .

我们也可以用表格表示一个策略：

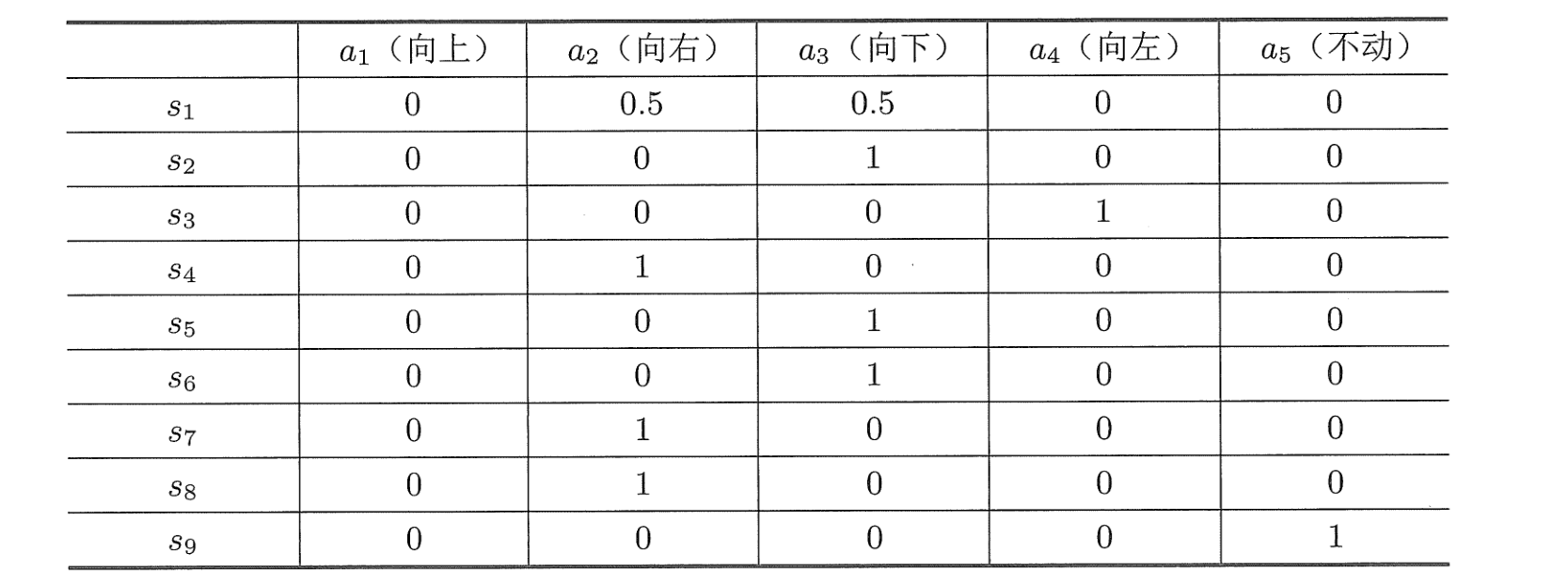
奖励 (reward)

奖励是 RL 当中最独特的概念，一般而言，当 agent 进行一个动作之后，可以人为给它奖励（惩罚）\(r\) ，当 \(r>0\) 时就是奖励，\(r<0\) 时就是惩罚，一般统一称为奖励.

例如：当 agent 状态转移到 \(s_{9}\) ，也就是目标区域时，就给 \(r=1\) 的奖励，进入禁止区域或者试图超出边界时，就给定 \(r=-1\) 的惩罚，其余情况下 \(r=0\) .

在这种情况下，agent 可能会到达目标后就停留在目标区域一直 +1+1+1..... .

更一般化的奖励过程还是可以用概率来说明，例如：

\[p(r\mid a_{1},s_{1}) \]

这个时候奖励也可能是随机的，agent 将会从中学习如何应对.

一个自然的问题就是：\(p(r\mid a_{1},s_{1})\) 是否还会是下一个状态的函数，换言之假如说 \(s_{1}\xrightarrow{a_{2}}s_{2}\) ，那么 \(p(r\mid a_{2},s_{1})\) 是否应该写为 \(p(r\mid a_{1},s_{1},s_{2})\) ？

这个问题实际上是非常有意义的，\(r\) 确实依赖于三者，但是 \(s_{2}\) 也同样依赖于 \(a_{1},s_{1}\) ，因此我们可以等效的建立起等式：
\(p(r\mid s,a) = \sum\limits_{s'}p(r\mid s,a,s')p(s'\mid s,a)\) .

轨迹、回报、回合

一条轨迹 (trajectory) 就是一个状态转移序列：

\[s_{1}\xrightarrow{a_{2}}s_{2}\xrightarrow{a_{3}}s_{5}\xrightarrow{a_{3}}s_{8}\xrightarrow{a_{2}}s_{9} \]

回报 (return) 就是这些即时奖励的求和，上面的轨迹的回报就是：

\[\mathrm{return} = 0+0+0+1 = 1 \]

轨迹也有可能无限长，例如

\[s_{1} \xrightarrow{a_{5}}s_{1}\xrightarrow{a_{5}}\cdots \]

一直停留在原地，此时的回报就是 \(\mathrm{return} = 0\) ，回报在此时可能会发散，例如：

\[s_{1}\xrightarrow{a_{2}}s_{2}\xrightarrow{a_{3}}s_{5}\xrightarrow{a_{3}}s_{8}\xrightarrow{a_{2}}s_{9} \xrightarrow{a_{5}} s_{9}\xrightarrow{a_{5}} \cdots \]

此时回报就会发散到 \(\infty\) . 为了解决这个问题，我们设定折扣因子 (discount rate) ，第 \(i\) 次动作的奖励就会施加 \(\gamma^{i-1}\) 的折扣因子，因此上述的回报就是

\[0 + \gamma 0+ \gamma^{2}0 + \gamma^{3}1 + \gamma^{4}1+\cdots = \gamma^{3} \frac{1}{1-\gamma} \]

然后，从初始状态到终止状态，这一套过程称为回合 (episode).

• 终止状态可以是一种吸收状态，比如设定 \(\mathcal{A}(s_{9}) = \left\lbrace a_{5} \right\rbrace\) ，也就是终点处只能够原地不动；
• 终止状态也可以设定为普通状态，这样就有可能出现“反复横跳”的情况.

Markov 决策过程 (Markov Decision Process, MDP)

Markov 决策过程是一种一般框架，它由如下的要素组合而成：

• 集合
  • 状态空间：\(\mathcal{S}\) .
  • 动作空间：\(\mathcal{A}(s), s\in \mathcal{S}\) .
  • 奖励集合：\(\mathcal{R}(s,a), s\in \mathcal{S}, a\in \mathcal{A}\) .
• 模型
  • 状态转移概率：从状态 \(s\) 采取动作 \(a\) ，转移到 \(s'\) 的概率为 \(p(s'\mid s,a)\) ，对于任意 \((s,a)\) ，都有 \(\sum\limits_{s'\in \mathcal{S}}p(s'\mid s,a)=1\) .
  • 奖励概率：在状态 \(s\) 采取动作 \(a\) 时，智能体获得奖励 \(r\) 的概率是 \(p(r\mid s,a)\) ，对于任意 \((s,a)\) ，都有 \(\sum\limits_{r\in \mathcal{R}(s,a)}p(r\mid s,a)=1\) 成立.
• 策略
  • 状态 \(s\) 下，agent 采取动作 \(a\) 的概率是 \(\pi(a\mid s)\) ，对于任意 \(s\in \mathcal{S}\) ，都有 \(\sum\limits_{a\in \mathcal{A}(s)}\pi(a\mid s)=1\) .
• Markov 性质
  • 即状态、奖励都有无记忆性，例如对于状态，\(p(s_{t+1}\mid s_{t},a_{t},s_{t-1},a_{t-1},\cdots,s_{1},a_{1}) = p(s_{t+1}\mid s_{t},a_{t})\) .

MDP 是 RL 当中最重要的一类框架，这里面 \(p(s'\mid s,a)\) 和 \(p(r\mid s,a)\) 称为模型 (model) ，模型可以是平稳的 (stationary) 或者非平稳的. 平稳的含义是模型不随时间变化而变化.