论文解读：EMNLP 2021-SimCSE: Simple Contrastive Learning of Sentence Embeddings

论文
代码

对于这篇经典论文的讲解已经有很多，这里推荐两个感觉讲的很清楚的讲解1、讲解2，相信看了这两篇论文后对整体的内容已经大致清楚，但是对于SimCSE如何减少各向异性的证明可能还会比较模糊（公式太多了/(ㄒoㄒ)/~~）。因此本文将会这部分进行比较详细的说明。参考自参考1、参考2

目录

• 各向异性说明
• 琴生不等式(Jensen's Inequality)
• alignment和uniformity
• 降低各向异性证明
• 损失函数的改进

各向异性说明

参考1中进行了很形象的说明，这里在重复一遍。

• 各向异性：词向量是有维度的，每个维度上基向量单位向量长度不一样，就是各向异性的。这样就会造成我们计算向量相似度的时候产生偏差，如下图是举例：
  

• 上图中，基向量是非正交(x,y)，且各向异性（基向量单位向量长度不一样），计算向量x1与x2的cos相似度为0，x1与x3的cos相似度为0(正交)，但是我们从几何角度上看，其实x1是与x3更相似的，所以导致计算相似度结果也会有问题。

琴生不等式(Jensen's Inequality)

• 举个很简单的例子，如果一个凹函数，例如\(y=x^2\).和一个凸函数例如\(y=log(x)\)
  

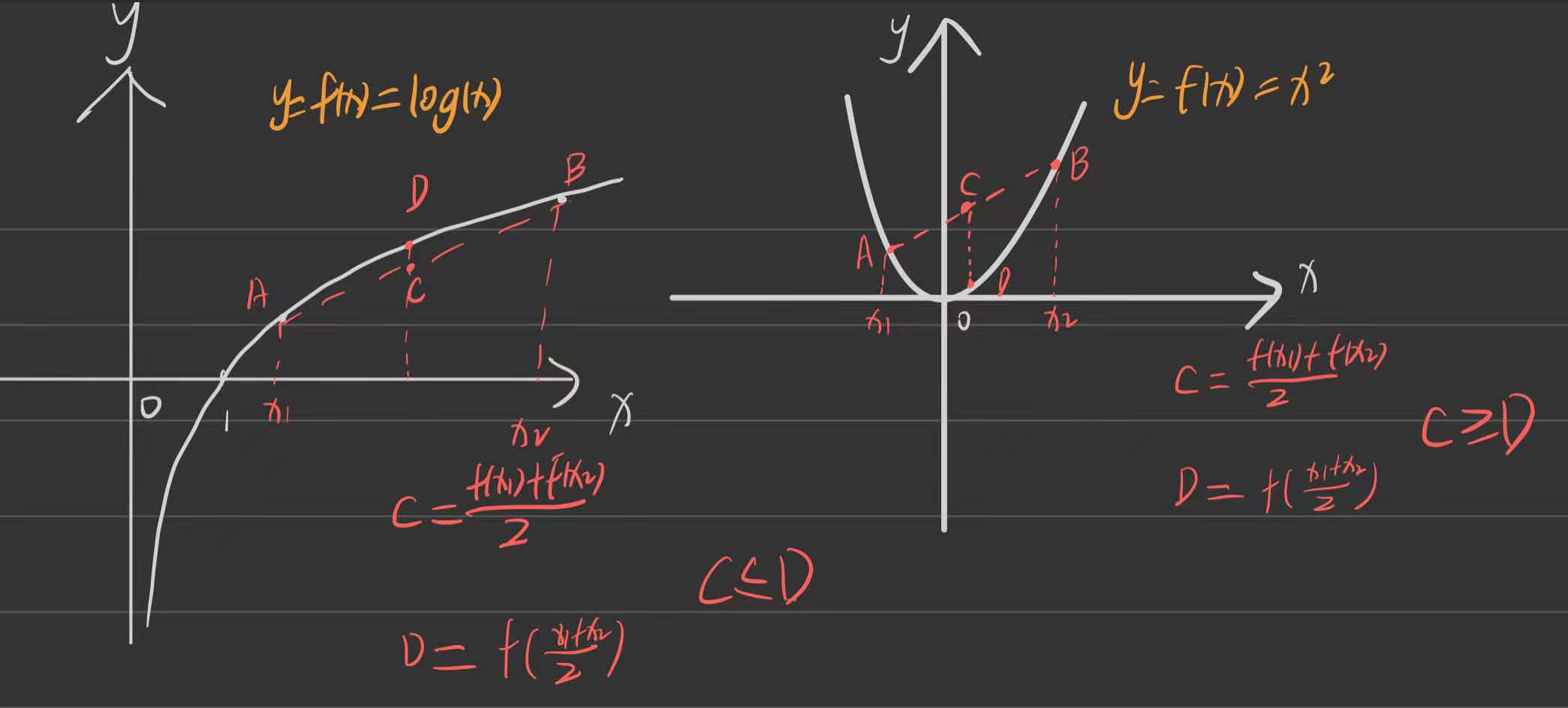
上图中，很显然对于凹函数：\(\frac{f(x1)+f(x2)}{2}\ge f(\frac{x1+x2}{2})\)，而对于凸函数正相反。将这个原理扩展到n个变量，就是琴生不等式。

alignment和uniformity

对比学习的目标是从数据中学习到一个优质的语义表示空间，那么如何评价这个表示空间的质量呢？在讲解1和讲解2已经介绍了所采用的alignment和uniformity，即对齐和均匀性两个标准。alignment计算距离正样本间的距离，而uniformity计算向量整体分布的均匀程度。我们希望这两个指标都尽可能低，也就是一方面希望正样本要挨得足够近，另一方面语义向量要尽可能地均匀分布在超球面上，因为均匀分布信息熵最高，分布越均匀则保留的信息越多，“拉近正样本，推开负样本”实际上就是在优化这两个指标。

• 对于alignment和uniformity分别可以用以下两个函数进行定义。

\[\ell_{\text {align }} \triangleq \underset{\left(x, x^{+}\right) \sim p_{\text {pos }}}{\mathbb{E}}\left\|f(x)-f\left(x^{+}\right)\right\|^{2} \]

\[\ell_{\text {uniform }} \triangleq \log \underset{x, y \stackrel{i . i d}{\sim} p_{\text {data }}}{\mathbb{E}} \quad e^{-2\|f(x)-f(y)\|^{2}} \]

降低各向异性证明

• 本文作者提出可以通过随机采样dropout mask来生成\({x^+_i}\)，在标准的Transformer中，dropout mask被放置在全连接层和注意力求和操作上，由于dropout mask是随机生成的，所以在训练阶段，将同一个样本分两次输入到同一个编码器中
  
  \(\begin{aligned} \ell_{i} &=-\log \frac{e^{\operatorname{sim}\left(\boldsymbol{h}_{i}^{(0)}, \boldsymbol{h}_{i}^{(1)}\right) / \tau}}{\sum_{j=1}^{N} e^{\operatorname{sim}\left(\boldsymbol{h}_{i}^{(0)}, \boldsymbol{h}_{j}^{(1)}\right) / \tau}} \\ &=-\log \left(e^{\operatorname{sim}\left(\boldsymbol{h}_{i}^{(0)}, \boldsymbol{h}_{i}^{(1)}\right) / \tau}\right)+\log \sum_{j=1}^{N} e^{\operatorname{sim}\left(\boldsymbol{h}_{i}^{(0)}, \boldsymbol{h}_{j}^{(1)}\right) / \tau} \\ &=-\frac{1}{\tau} \operatorname{sim}\left(\boldsymbol{h}_{i}^{(0)}, \boldsymbol{h}_{i}^{(1)}\right)+\log \sum_{j=1}^{N} e^{\operatorname{sim}\left(\boldsymbol{h}_{i}^{(0)}, \boldsymbol{h}_{j}^{(1)}\right) / \tau} \end{aligned}\)

上式就是模型的训练目标（损失函数），经过化简(log与e抵消)可以得到上面的结果，上面的结果可以进一步进行如下变形。

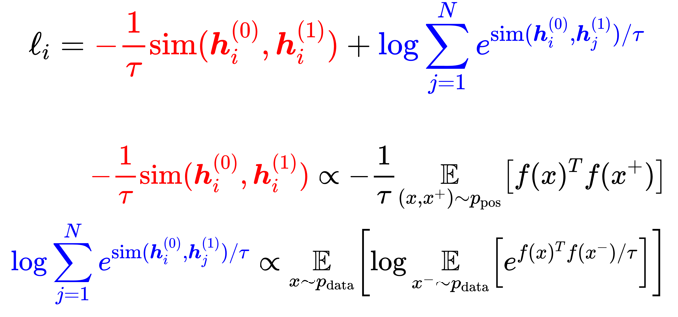
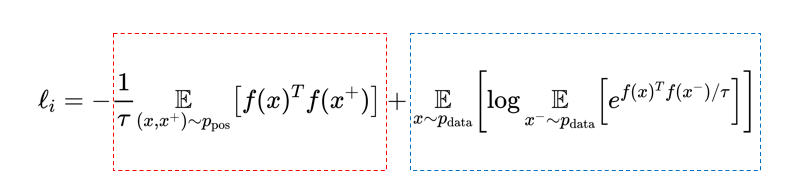
• 如上式，Wang and Isola (2020)证明了当负样本数量趋于无穷大时，对比学习的训练目标可以分别正比于如上两个式子，渐近表示为下式，其中E代表的是求期望。
  

• 其中第一项表示拉近正样本，第二项表示推开负样本，其中两个f相乘代表着两个向量之间的内积，那么内积越大就代表着距离越近。所以红线框中的内容是代表的是与正样本之间的距离，因此要足够大(即两个向量相近)，同理蓝色线框要足够的小。借助Jensen不等式进一步推导第二项的下界，结果如下：

• 我们只需把f(x)看作凸函数log(x)即可化解出结果。其中hi代表的是一个句向量，体现在矩阵中代表某一行。我们希望蓝色框越小越好，那么两个内积和一定越来越小

但是需要指出，其实\(h^T_i h_j\)位置并不对，但是只需最后可以用矩阵内积来表示即可。更详细的内容可以看参考2。

损失函数的改进

这是我在阅读arxiv论文时发现的一篇文章，通过很简单的加入高斯噪声的方法，解决对比学习对增加batchsize不敏感的问题。

• 目标：理论上在 unsup-SimCSE 中使用更大的批次以获得更充分的样本比较并避免过度拟合。但是，增加批量大小并不总是会带来改进，反而会在批量大小超过阈值时导致性能下降。通过统计观察，我们发现这可能是由于增加批量大小后引入了低置信度负对。为了缓解这个问题，我们在 InfoNCE 损失函数上引入了一种简单的平滑策略，称为高斯平滑 InfoNCE（GS-InfoNCE）。

• 方法：作者认为这个原因是由于增加batchsize后加入了很多重复的样本，而当这些样本互为负样本时(因为实际上的损失函数要对一个batchsize内的所有取平均值)会造成混乱(因为实际上是很相似的)。作者通过高斯噪声的加入(相当于加入一个绝对负样本)，确保了即使有重复样本的加入，也可以达到互相远离的效果。

\[\ell_{i}=-\log \frac{e^{\operatorname{sim}\left(\mathbf{h}_{i}, \mathbf{h}_{i}^{+}\right) / \tau}}{\sum_{j=1}^{N} e^{\operatorname{sim}\left(\mathbf{h}_{j}, \mathbf{h}_{i}\right) / \tau}+\lambda \cdot \sum_{k=1}^{M} e^{\operatorname{sim}\left(\mathbf{g}_{k}, \mathbf{h}_{i}\right) / \tau}} \]

• 代码：
  

• 结果显示确实比原本的有所提高，由于实现比较简单，可以供大家尝试一下。