树链剖分

将树上问题转到序列上，转而方便用数据结构维护

重子节点：表示其子节点中子树最大的子结点

如果有多个子树最大的子结点，取其一

如果没有子节点，就无重子节点

轻子节点：表示剩余的所有子结点

重边：从这个结点到重子节点的边为

轻边：到其他轻子节点的边为

重链：若干条首尾衔接的重边构成

把落单的结点也当作重链，那么整棵树就被剖分成若干条重链

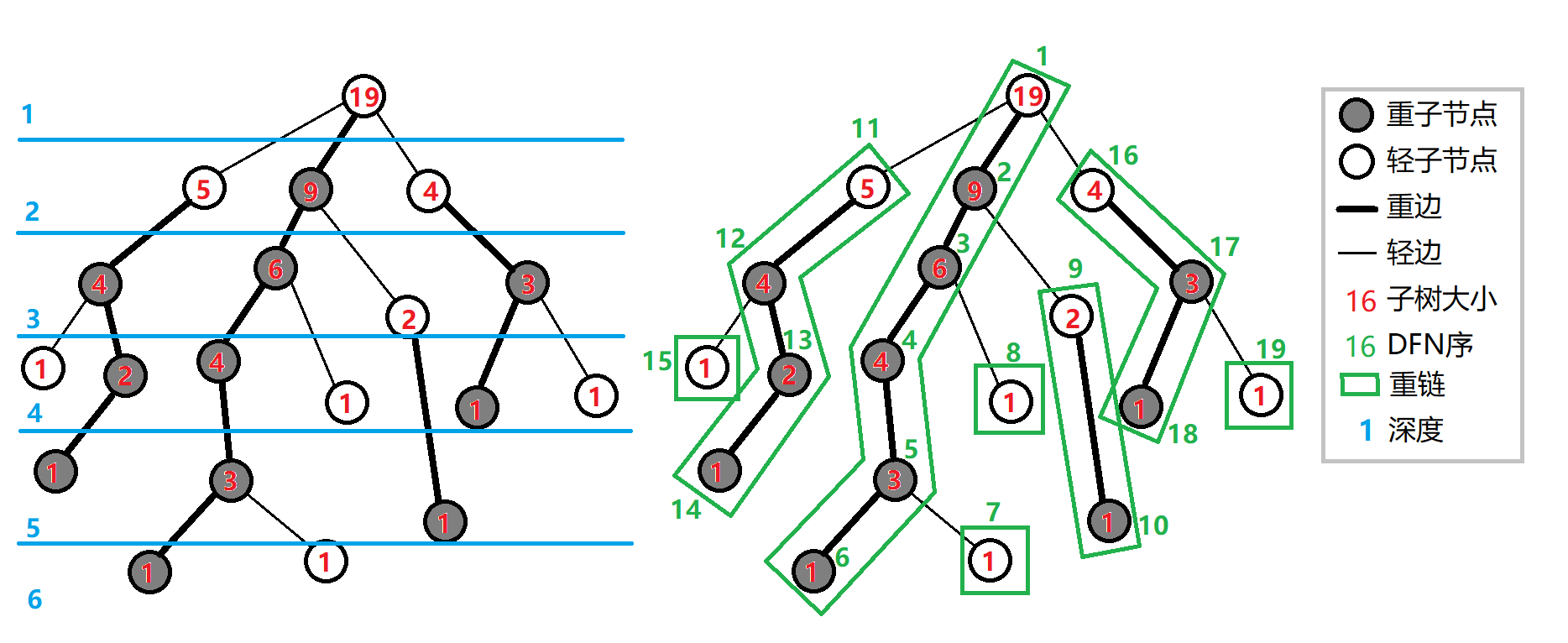
树上每个节点都属于且仅属于一条重链

在剖分时，重边优先遍历，最后树的 \(DFS\) 序上，重链内的 \(DFS\) 序是连续的

记 \(son_x\) 表示重儿子，\(top_x\) 表示 \(x\) 所在重链的 \(top\) 节点（\(dep\) 最浅的）

我们向下经过一条轻边时，所在子树的大小至少会除以二！！

blog1

P3384 【模板】重链剖分/树链剖分

第一次 \(dfs\)，处理 \(dep\)，\(fa\)，\(sz\)，\(son\)
第二次 \(dfs\)，处理 \(dfn\)，\(top\)
对 \(dfn\) 建立线段树

\(1\) 中重儿子判定为 \(son_v^{max}\)

\(2\) 中注意处理 \(dfn\) 的时候，要把节点的权值复制到 \(w\)，这样建树才是 \(dfn \Leftrightarrow tr\) 的正确映射

\(3\) 中对于修改子树和查询子树是显然的

对于路径修改和查询，我们不妨考虑 \(lca\) 的过程，并在找 \(lca\) 时完成对路径的修改和查询

若 \(x,y\) 在不同重链中，选取链头深度较大的点，让其跳过链头到达链头的父亲

若 \(x,y\) 在同一重链中，深度小的点即为 \(LCA\)

下面为找 \(lca\) 的简易代码

int lca(int x,int y)
{
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y]) swap(x,y);
	return x;
}

每次跳链重/轻链，子树 \(sz\) \(\times 2\)，复杂度 \(O(\log n)\)，每次修改查询 \(O(\log n)\)

\(O(n\log n+m\log^2 n)\)

#include<bits/stdc++.h>
#define int long long
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x])
using namespace std;

const int N=1e5+10;
int n,m,T,Q,op,u,v,x,y,z,stm;
int a[N],w[N],fa[N],dep[N],son[N],sz[N],top[N],dfn[N];
vector<int> as[N];
struct node{
	int l,r;
	int v,add;
}tr[N*4];

int fr(){
    int x=0,flag=1;
    char ch=getchar();
    while(ch<'0' || ch>'9'){
        if(ch=='-') flag=-1;
        ch=getchar();
    }
    while(ch>='0' && ch<='9'){
        x=x*10+(ch-'0');
        ch=getchar();
    }
    return x*flag;
}
void fw(int x){
	if(x<0) putchar('-'),x=-x;
    if(x>9) fw(x/10);
    putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}

void init(int x,int rt)
{
	dep[x]=dep[rt]+1;
	fa[x]=rt,sz[x]=1;
	
	go(v)
	{
		if(v==rt) continue;
		init(v,x);
		sz[x]+=sz[v];
		if(sz[son[x]]<sz[v]) son[x]=v;
	}
}

void dfs(int x,int Top)
{
	dfn[x]=++stm;
	w[stm]=a[x];
	top[x]=Top;
	if(!son[x]) return;
	dfs(son[x],Top);
	go(v) if(!dfn[v]) dfs(v,v);
}

void chf(int idx)
{
	node &t=tr[idx],&ls=tr[idx<<1],&rs=tr[idx<<1|1];
	t.v=(ls.v+rs.v)%Q;
}

void chs(int idx)
{
	node &t=tr[idx],&ls=tr[idx<<1],&rs=tr[idx<<1|1];
	if(t.add)
	{
		(ls.add+=t.add)%=Q,(rs.add+=t.add)%=Q;
		(ls.v+=(ls.r-ls.l+1)*t.add)%=Q;
		(rs.v+=(rs.r-rs.l+1)*t.add)%=Q;
		t.add=0;
	}
}

void build(int ql,int qr,int idx)
{
	tr[idx]={ql,qr};
	if(ql==qr)
	{
		tr[idx].v=w[ql]%Q;
		return;
	}
	int mid=(ql+qr)>>1;
	build(ql,mid,idx<<1);
	build(mid+1,qr,idx<<1|1);
	chf(idx);
}

void modify(int ql,int qr,int idx,int x)
{
	node &t=tr[idx];
	if(ql<=t.l && qr>=t.r)
	{
		(t.add+=x)%=Q;
		(t.v+=(t.r-t.l+1)*x)%=Q;
		return;
	}
	chs(idx);
	int mid=(t.l+t.r)>>1;
	if(ql<=mid) modify(ql,qr,idx<<1,x);
	if(qr>mid) modify(ql,qr,idx<<1|1,x);
	chf(idx);
}

int query(int ql,int qr,int idx)
{
	node &t=tr[idx];
	if(ql<=t.l && qr>=t.r)
		return t.v;
	chs(idx);
	int mid=(t.l+t.r)>>1,s=0;
	if(ql<=mid) (s+=query(ql,qr,idx<<1))%=Q;
	if(qr>mid) (s+=query(ql,qr,idx<<1|1))%=Q;
	return s;
}

void modify(int x,int y,int v)
{
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		modify(dfn[top[x]],dfn[x],1,v);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y]) swap(x,y);
	modify(dfn[x],dfn[y],1,v);
}

int query(int x,int y)
{
	int res=0;
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		(res+=query(dfn[top[x]],dfn[x],1))%=Q;
		x=fa[top[x]];
	}
	if(dep[x]>dep[y]) swap(x,y);
	(res+=query(dfn[x],dfn[y],1))%=Q;
	return res;
}

signed main()
{
	n=fr(),m=fr(),T=fr(),Q=fr();
	for(int i=1;i<=n;i++) a[i]=fr();
	for(int i=1;i<n;i++)
	{
		u=fr(),v=fr();
		as[u].pb(v),as[v].pb(u);
	}
	
	init(T,0);
	dfs(T,T); //根的链头设成自己
	
	build(1,n,1);
	for(int i=1;i<=m;i++)
	{
		op=fr();
		if(op==1) x=fr(),y=fr(),z=fr(),modify(x,y,z%Q);
		else if(op==2) x=fr(),y=fr(),fw(query(x,y)),nl;
		else if(op==3) x=fr(),z=fr(),modify(dfn[x],dfn[x]+sz[x]-1,1,z%Q);
		else x=fr(),fw(query(dfn[x],dfn[x]+sz[x]-1,1)),nl;
	}

	return 0;
}

P2146 [NOI2015] 软件包管理器

模板题

线段树的 \(add\) 标记可以先初始化设为 \(-1\)，方便判断

判断改变的量，就是两次 \(tr[1].v\) 的差值！！

\(dfs\) 的时候一定要判断 \(!dfn_v\)

P3979 遥远的国度

没有操作 \(1\) 就是裸的树剖

考虑换根的影响

首先路径修改不受影响

子树最小值需要分情况讨论

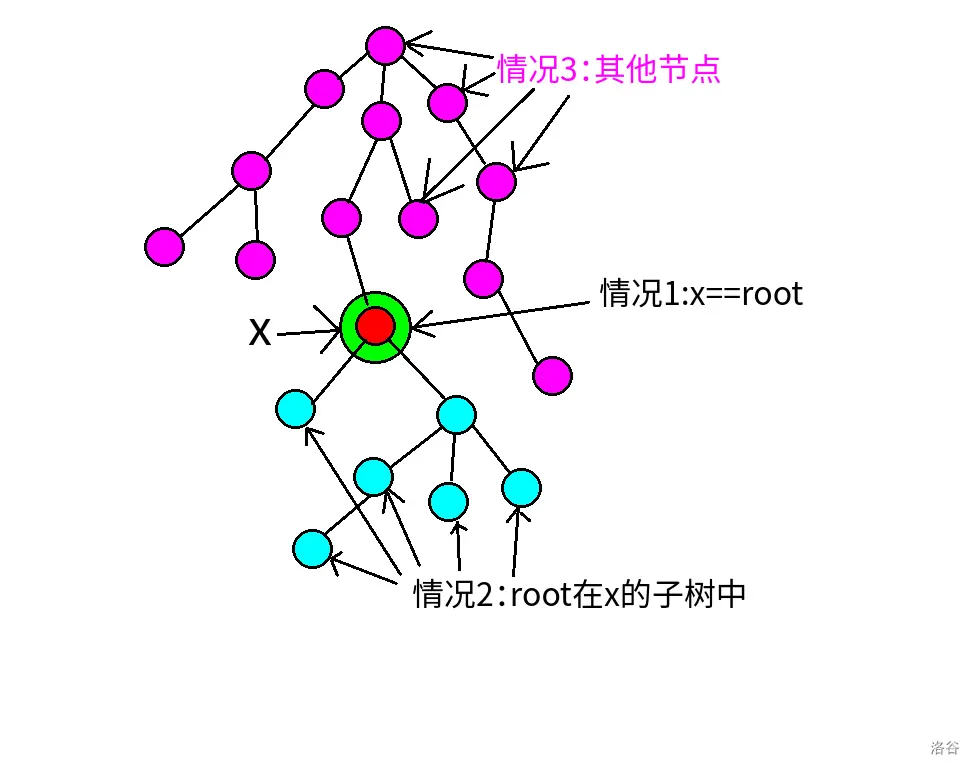
tr[1].v
\(x\) 的真正子树是包括除了 \(root\) 方向上的子树之外其他所有节点
没有影响

如何判断是否在子树内部？\(LCA\) 即可

#include<bits/stdc++.h>
#define int long long
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x])
using namespace std;

const int N=3e5+10;
int n,m,u,v,T,R,op,x,y,z,stm;
int a[N],w[N],fa[N],dep[N],son[N],sz[N],top[N],dfn[N];
vector<int> as[N];
struct node{
	int l,r;
	int v,add;
}tr[N*4];

int fr(){
    int x=0,flag=1;
    char ch=getchar();
    while(ch<'0' || ch>'9'){
        if(ch=='-') flag=-1;
        ch=getchar();
    }
    while(ch>='0' && ch<='9'){
        x=x*10+(ch-'0');
        ch=getchar();
    }
    return x*flag;
}
void fw(int x){
	if(x<0) putchar('-'),x=-x;
    if(x>9) fw(x/10);
    putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}

void init(int x,int rt)
{
	dep[x]=dep[rt]+1;
	fa[x]=rt,sz[x]=1;
	
	go(v)
	{
		if(v==rt) continue;
		init(v,x);
		sz[x]+=sz[v];
		if(sz[son[x]]<sz[v]) son[x]=v;
	}
}

void dfs(int x,int Top)
{
	dfn[x]=++stm;
	w[stm]=a[x];
	top[x]=Top;
	if(!son[x]) return;
	dfs(son[x],Top);
	go(v) if(!dfn[v]) dfs(v,v);
}

void chf(int idx)
{
	node &t=tr[idx],&ls=tr[idx<<1],&rs=tr[idx<<1|1];
	t.v=min(ls.v,rs.v);
}

void chs(int idx)
{
	node &t=tr[idx],&ls=tr[idx<<1],&rs=tr[idx<<1|1];
	if(t.add)
	{
		ls.v=rs.v=t.add;
		ls.add=rs.add=t.add;
		t.add=0;
	}
}

void build(int ql,int qr,int idx)
{
	tr[idx]={ql,qr};
	if(ql==qr)
	{
		tr[idx].v=w[ql];
		return;
	}
	
	int mid=(ql+qr)>>1;
	build(ql,mid,idx<<1);
	build(mid+1,qr,idx<<1|1);
	chf(idx);
}

void modify(int ql,int qr,int idx,int x)
{
	node &t=tr[idx];
	if(ql<=t.l && qr>=t.r)
	{
		t.v=t.add=x;
		return;
	}
	
	chs(idx);
	int mid=(t.l+t.r)>>1;
	if(ql<=mid) modify(ql,qr,idx<<1,x);
	if(qr>mid) modify(ql,qr,idx<<1|1,x);
	chf(idx);
}

int query(int ql,int qr,int idx)
{
	if(ql>qr) return 1e18;
	node &t=tr[idx];
	if(ql<=t.l && qr>=t.r)
		return t.v;
	
	if(t.add) return t.add;
	int mid=(t.l+t.r)>>1,mt=1e18;
	if(ql<=mid) mt=min(mt,query(ql,qr,idx<<1));
	if(qr>mid) mt=min(mt,query(ql,qr,idx<<1|1));
	return mt;
}

void modify(int x,int y,int v)
{
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		modify(dfn[top[x]],dfn[x],1,v);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y]) swap(x,y);
	modify(dfn[x],dfn[y],1,v);
}

int lca(int x,int y)
{
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y]) swap(x,y);
	return x;
}

int query(int x)
{
	if(x==R) return tr[1].v; //情况 1
	else if(lca(x,R)!=x) return query(dfn[x],dfn[x]+sz[x]-1,1);
	else {go(v) {if(v!=fa[x] && lca(v,R)==v) return min(query(1,dfn[v]-1,1),query(dfn[v]+sz[v],n,1));}}
}

signed main()
{
	n=fr(),m=fr();
	for(int i=1;i<n;i++)
	{
		u=fr(),v=fr();
		as[u].pb(v),as[v].pb(u);
	}
	for(int i=1;i<=n;i++) a[i]=fr();
	R=T=fr();
	
	init(T,0);
	dfs(T,T);
	build(1,n,1);
	
	for(int i=1;i<=m;i++)
	{
		op=fr();
		if(op==1) R=fr();
		else if(op==2) x=fr(),y=fr(),z=fr(),modify(x,y,z);
		else fw(query(fr())),nl;
	}
	
	return 0;
}

posted @ 2023-07-24 09:48 xyzfrozen 阅读(17) 评论(0) 收藏举报

刷新页面返回顶部

xyzfrozen

Everything and I are absurd silence

树链剖分

树链剖分

公告