BZOJ 2725 [Violet 6]故乡的梦

BZOJ 2725 [Violet 6]故乡的梦

如果不是这个题是 \(Violet\)，打死我也不会写这题的

去掉 \((u,v)\)，我们不难想到一个类似处理前缀和后缀的方法

首先无向图转有向图，我们跑出一条 \([S,T]\) 的最短路，定义为路径 \(P\)

对于边不在 \(P\) 上的情况是显然的，讨论在上面的

类似 [GXOI/GZOI2019] 旅行者 这个题的 \(O(\log n)\) 做法，[USACO15JAN] Grass Cownoisseur G 这个题两次 \(dij\) 的做法

先给 \(P\) 上的点编号

考虑答案路径一定是 \([S,a,x,y,b,T]\)

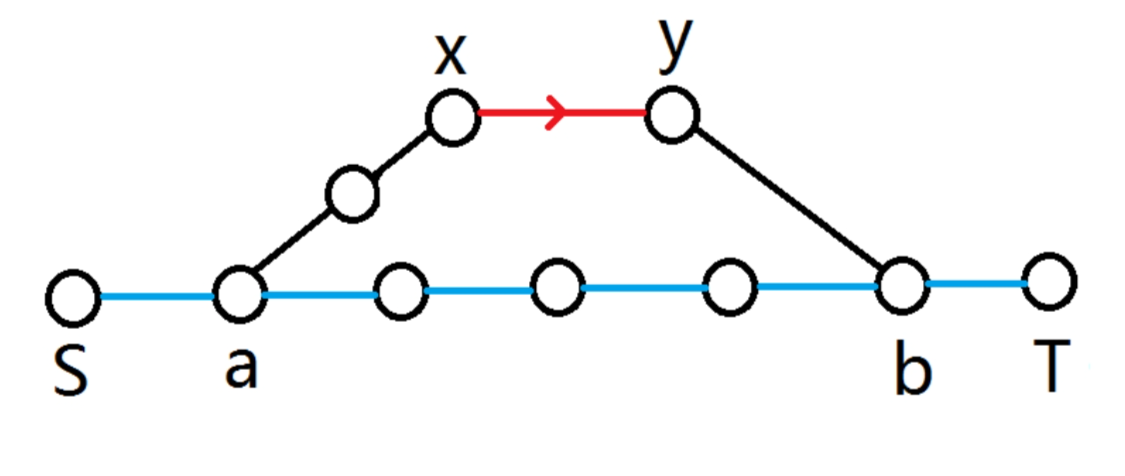
我们预处理枚举所有边 \((x,y)\)，强制让最短路经过它

这条边产生的贡献，即什么时候会被算入最短路

设 \(DS_i\;DT_i\) 表示 \(S\;T\) 到 \(i\) 的最短路

\(L_x\;R_x\) 表示 \(x\) 到 \(P\) 上离 \(S/T\) 最近的点的编号（从 \([S,T]\) 重新编过号后的）

对于 \((x,y)\)，相当于删掉 \([a,b]\) 之间的边它就有可能产生答案，我们把每条边转成点，绑定在它 \(id\) 较小的点上

每次枚举边相当于对 \([L_x,R_x-1]\) 的做区间 \(Min\)，每次询问相当于单点查询，用线段树来做

\(O(n\log n+m\log n+q)\)

注意 \(memset\) \(d_g\) 的时候是 \(sizeof\,d_g\) ！！！

#include<bits/stdc++.h>
#define int long long
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x])
using namespace std;

const int N=4e5+10;
int n,m,Q,u,v,w,S,T,len,inf=0x3f3f3f3f3f3f3f3f;
int d[4][N],p[N],pre[N],in[N],q[N];
int P[N],id[N],ans[N],L[N],R[N];
vector<pi> as[N];
vector<int> G[N];
struct Edge{int u,v,w;}E[N];
struct node{int l,r,v;}tr[N*4];

int fr(){
    int x=0,flag=1;char ch=getchar();
    while(ch<'0' || ch>'9'){
        if(ch=='-') flag=-1;
        ch=getchar();
    }
    while(ch>='0' && ch<='9') x=x*10+(ch-'0'),ch=getchar();
    return x*flag;
}
void fw(int x){
	if(x<0) putchar('-'),x=-x;
    if(x>9) fw(x/10);
    putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
bool ck(int x,int y){return id[x]&&id[y]&&(id[x]==id[y]+1 || id[y]==id[x]+1);}

void dij(int S,int g)
{
	priority_queue<pi,vector<pi>,greater<pi>> q;
	q.push({0,S});
	memset(d[g],0x3f,sizeof d[g]);
	memset(p,0,sizeof p);
	d[g][S]=0;
	
	while(q.size())
	{
		auto t=q.top();
		q.pop();
		
		int x=t.second;
		if(p[x]) continue;
		p[x]=1;
		
		go(it)
		{
			int v=it.first,w=it.second;
			if(d[g][v]>d[g][x]+w) d[g][v]=d[g][x]+w,pre[v]=x,q.push({d[g][v],v});
		}
	}
}

void get_path()
{
	dij(S,1);
	if(d[1][T]==inf)
	{
		Q=fr();
		while(Q--) puts("Infinity");
		exit(0);
	}
	
	for(int x=T;pre[x];x=pre[x]) P[++len]=x;
	P[++len]=S,reverse(P+1,P+1+len);
	for(int i=1;i<=len;i++) id[P[i]]=i;
	
	for(int i=1;i<=n;i++) L[i]=N;
	for(int i=1;i<=len;i++) L[P[i]]=i;
	for(int i=1;i<=m;i++)
	{
		u=E[i].u,v=E[i].v,w=E[i].w;
		if(d[1][u]+w==d[1][v]) in[v]++,G[u].pb(v);
		if(d[1][v]+w==d[1][u]) in[u]++,G[v].pb(u);
	}
	
	int hh=0,tt=-1;
	q[++tt]=S;
	while(hh<=tt)
	{
		int x=q[hh++];
		for(auto &v:G[x])
		{
			if(!id[v]) L[v]=min(L[v],L[x]);
			if(!(--in[v])) q[++tt]=v;
		}
	}
	
	dij(T,2);
	for(int i=1;i<=n;i++) G[i].clear(),in[i]=0;
	for(int i=1;i<=len;i++) R[P[i]]=i;
	for(int i=1;i<=m;i++)
	{
		u=E[i].u,v=E[i].v,w=E[i].w;
		if(d[2][u]+w==d[2][v]) in[v]++,G[u].pb(v);
		if(d[2][v]+w==d[2][u]) in[u]++,G[v].pb(u);
	}
	
	hh=0,tt=-1;
	q[++tt]=T;
	while(hh<=tt)
	{
		int x=q[hh++];
		for(auto &v:G[x])
		{
			if(!id[v]) R[v]=max(R[v],R[x]);
			if(!(--in[v])) q[++tt]=v;
		}
	}
}

void build(int ql,int qr,int idx)
{
	tr[idx]={ql,qr,inf};
	if(ql==qr) return;
	int mid=(ql+qr)>>1;
	build(ql,mid,idx<<1);
	build(mid+1,qr,idx<<1|1);
}

void modify(int ql,int qr,int idx,int x)
{
	node &t=tr[idx];
	if(ql<=t.l && qr>=t.r) {t.v=min(t.v,x);return;}
	int mid=(t.l+t.r)>>1;
	if(ql<=mid) modify(ql,qr,idx<<1,x);
	if(qr>mid) modify(ql,qr,idx<<1|1,x);
}

void chs(int idx)
{
	node &t=tr[idx];
	if(t.l==t.r) {ans[t.l]=t.v;return;}
	node &ls=tr[idx<<1],&rs=tr[idx<<1|1];
	ls.v=min(ls.v,t.v),rs.v=min(rs.v,t.v);
	chs(idx<<1),chs(idx<<1|1);
}

void solve()
{
	build(1,len-1,1);
	for(int i=1;i<=m;i++)
	{
		u=E[i].u,v=E[i].v,w=E[i].w;
		if(ck(u,v)) continue;
		if(L[u]!=N && R[v] && L[u]<R[v]) modify(L[u],R[v]-1,1,d[1][u]+w+d[2][v]);
		if(L[v]!=N && R[u] && L[v]<R[u]) modify(L[v],R[u]-1,1,d[1][v]+w+d[2][u]);
	}
	chs(1);
}

signed main()
{
	n=fr(),m=fr();
	for(int i=1;i<=m;i++)
	{
		u=fr(),v=fr(),w=fr();
		as[u].pb({v,w}),as[v].pb({u,w}),E[i]={u,v,w};
	}
	
	S=fr(),T=fr();
	if(S==T)
	{
		Q=fr();
		while(Q--) puts("0");
		return 0;
	}
	get_path();
	solve();
	
	Q=fr();
	for(int i=1;i<=Q;i++)
	{
		u=fr(),v=fr();
		if(ck(u,v))
		{
			if(ans[min(id[u],id[v])]==inf) puts("Infinity");
			else fw(ans[min(id[u],id[v])]),nl;
		}
		else fw(d[1][T]),nl;
	}

	return 0;
}