LOJ535「LibreOJ Round #6」花火

LOJ535「LibreOJ Round #6」花火

不难发现最小交换次数就是你逆序对数

哪次用这个随便交换和答案无关，我们考虑第一次用

暴力就是 \(O(n^2\log n)\)

直接枚举点对 \((i,j)\,[a_i \lt a_j][i \lt j]\)

能减少的逆序对数就是 \(2\) 倍，\([i+1,j-1]\) 区间内 \([a_j+1,a_i-1]\) 的个数

这个证明显然 \([1,i-1]\;[j+1,n]\) 都无影响，\([i,j]\) 不用考虑比 \(a_i\) 大的数，比 \(a_j\) 小的数，剩下的推下即可

考虑降到 \(O(n\log n)\)

不妨把每个点放到一个平面直角坐标系上！！！

类似下图这种情况，枚举矩形两角，求包含点数最多的矩形包含的点数

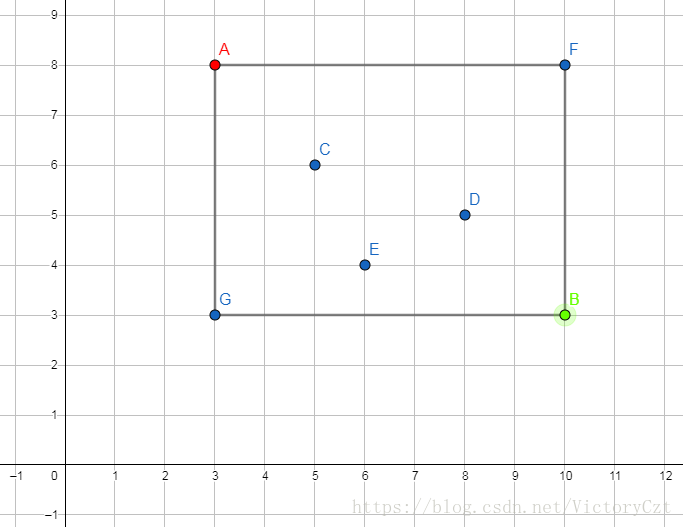
我们考虑如何 \(O(n\log n)\) 内求答案

对于下图这种情况，\(C\) 比 \(A\) 更优

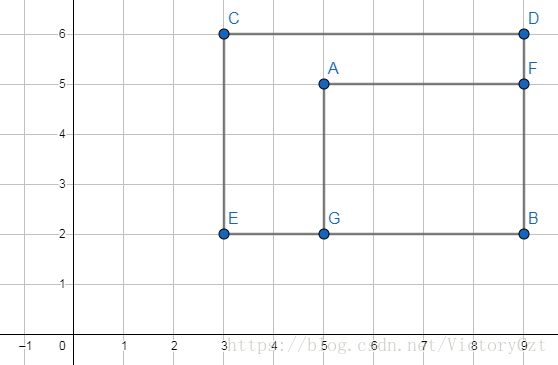
\(E\) 比 \(C\) 更优

则被选择的左上角和右下角一定形似

这个预处理 \(O(n)\)，可以单调栈也可以维护左侧最大值和右侧最小值，证明显然，如左侧只要下降，肯定不如之前上升的峰值的点

我们记这些点形成的序列为 \(L\;R\)

没法枚举矩形，但我们可以枚举点

这个点对哪些矩形产生贡献？左上方的点（矩阵左上角），右下方的点（矩阵右下角）这样的组合方案有贡献

这样的点数 \(L\) \(R\) 上一段连续的点，设左上方最左侧能成为左端点的点为 \(l\) 右端点为 \(r\)

这只要矩形两角在 \([l,i-1]\)，\([i+1,r]\) 区间内的，都对矩形有贡献

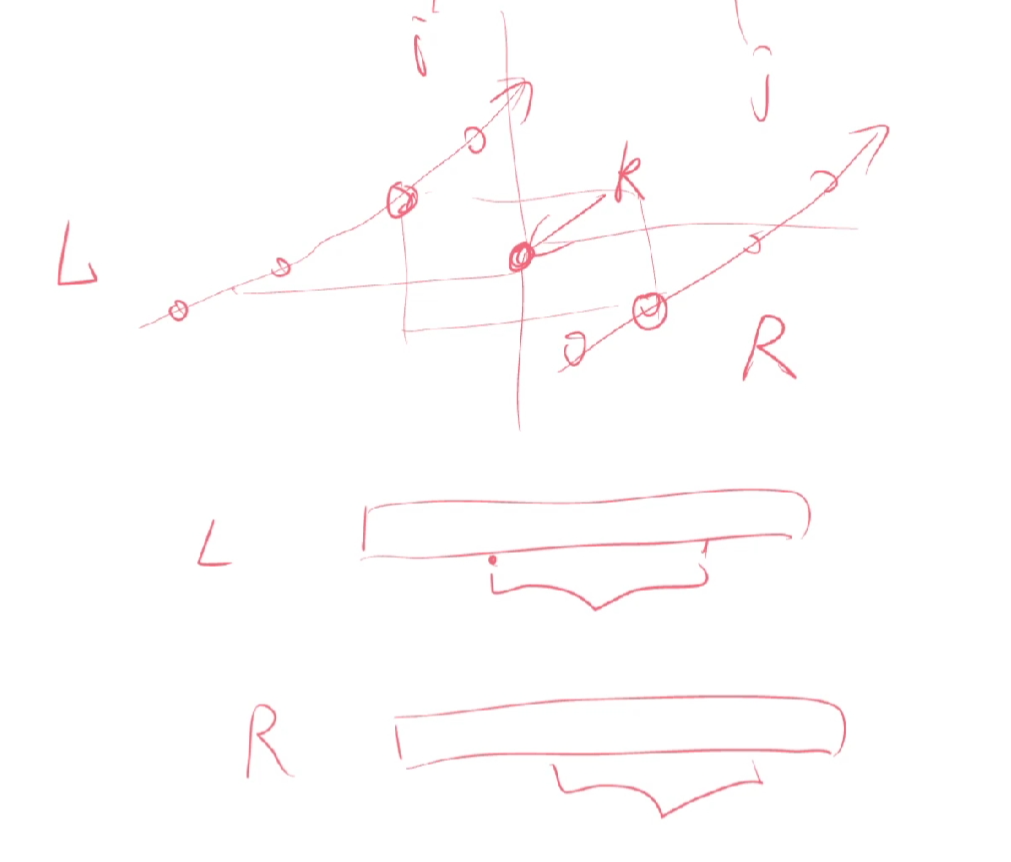
矩形不好计算，我们考虑再次对 \(L\)，\(R\) 建立平面直角坐标系

则用点对 \((x,y)\) 表述左上角在 \(x\) 右下角在 \(y\) 的矩形

则这个点产生的贡献作用在 \((l\sim i-1,i+1 \sim r)\) 内的点

转化为 \(L\;R\) 坐标系内，求一个点被矩形包含数量的最大值

二维点求最大矩形数，扫描线即可

const int N=3e5+10;
int n,ans,res;
int a[N],mxl[N],mnr[N];
struct Oper{int l,r,x;};
vector<Oper> op[N];

struct Bit{
	int s[N];
	void add(int i,int x){for(;i<=n;i+=i&(-i)) s[i]+=x;}
	int query(int i)
	{
		int res=0;
		for(;i;i-=i&(-i)) res+=s[i];
		return res;
	}
}bit;

struct Seg{
	struct node{
		int l,r;
		int maxt,add;
	}tr[N*4];
	
	void chf(int idx)
	{
	    node &t=tr[idx],&ls=tr[idx<<1],&rs=tr[idx<<1|1];
	    t.maxt=max(ls.maxt,rs.maxt);
	}
	
	void chs(int idx)
	{
	    node &t=tr[idx],&ls=tr[idx<<1],&rs=tr[idx<<1|1];
	    if(t.add)
	    {
			ls.add+=t.add,rs.add+=t.add;
		    ls.maxt+=t.add,rs.maxt+=t.add;
		    t.add=0;
		}
	}
	
	void build(int l,int r,int idx)
	{
	    tr[idx]={l,r};
	    if(l==r) return;
	    int mid=(l+r)>>1;
	    build(l,mid,idx<<1);
	    build(mid+1,r,idx<<1|1);
	    chf(idx);
	}
	
	void modify(int ql,int qr,int idx,int x)
	{
	    node &t=tr[idx];
	    if(ql<=t.l && qr>=t.r)
	    {
	        t.add+=x,t.maxt+=x;
	        return;
	    }
	    
	    chs(idx);
	    int mid=(t.l+t.r)>>1;
	    if(ql<=mid) modify(ql,qr,idx<<1,x);
	    if(qr>mid) modify(ql,qr,idx<<1|1,x);
	    chf(idx);
	}
}seg;

signed main()
{
	n=fr();
	for(int i=1;i<=n;i++) a[i]=fr();
	for(int i=1;i<=n;i++) mxl[i]=max(mxl[i-1],a[i]);
	mnr[n]=a[n];
	for(int i=n-1;i;i--) mnr[i]=min(mnr[i+1],a[i]);
	
	for(int i=1;i<=n;i++)
		res+=bit.query(n)-bit.query(a[i]),bit.add(a[i],1);
	
	for(int i=1;i<=n;i++)
	{
		int l=lower_bound(mxl+1,mxl+i,a[i])-mxl;
		int r=lower_bound(mnr+i,mnr+n+1,a[i])-mnr;
		if(l<i && r>i) op[l].pb({i+1,r,1}),op[i].pb({i+1,r,-1});
	}
	
	seg.build(1,n,1);
	for(int i=1;i<=n;i++)
	{
		for(auto v:op[i]) seg.modify(v.l,v.r,1,v.x);
		ans=max(ans,seg.tr[1].maxt);
	}
	fw(res-(ans<<1));

	return 0;
}