康托展开与逆康托展开

康托展开

求 \(1\sim N\) 的一个给定全排列在所有 \(1\sim N\) 全排列中的排名。结果对 \(998244353\) 取模

排名为字典序表示比它小的排列数 \(+1\)

\(1\le N\le 1000000\)

考虑一个类似数位 \(dp\) 的方法

从最高位开始，设当前位为 \(x\)，那么后面比它小的就是 \([1,...,x][?????]\) 后面任选

那么排名就要加上 \(x-1-cnt \times rest!\)

\(cnt\) 为前面比它小的数的个数，每个数只能用一次，这个用树状数组 \(\log n\)

\(rest\) 表示 \(?\) 的个数

\(O(n\log n)\)

---

\(eg:\)

P5367 【模板】康托展开

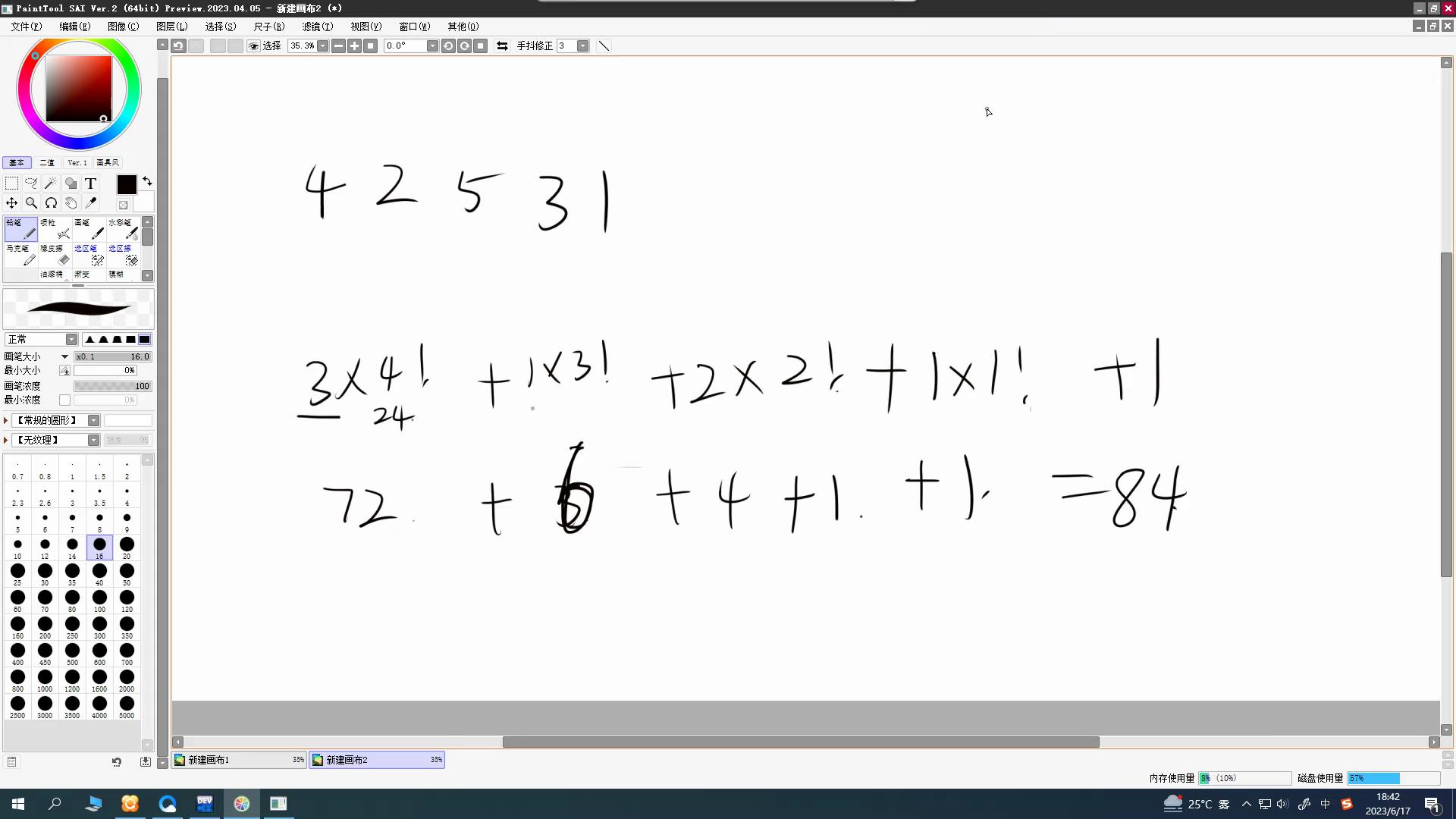
const int N=1e6+10,Q=998244353;
int n,ans;
int fac[N],s[N];

void add(int i,int x){for(;i<=n;i+=i&-i) s[i]+=x;}
int query(int i)
{
	int res=0;
	for(;i;i-=i&-i) res+=s[i];
	return res;
}

signed main()
{
	n=fr();
	fac[0]=1;
	for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%Q;
	for(int i=1;i<=n;i++)
	{
		int x=fr();
		int cnt=query(x-1),rest=n-i;
		ans=(ans+(x-1-cnt)*fac[rest]%Q)%Q;
		add(x,1);
	}
	fw(ans+1);
	return 0;
}

---

逆康托展开

Permutation

对于一个给定的 \(k\) ，求将自然数 \(1\) ~\(k\) 所有的排列按照字典序从小到大排序后位于第 \(n\) 的排列。排序从 \(0\) 开始编号

由于\(n\) 有可能很大，所以现在将给你 \(k\) 个数，分别为 \(S_1\) ，\(S_2\) ，……，\(S_k\) ，规定 \(n\) 的计算方式为

\[n=\sum_{i=1}^k S_i \times (k-i)! \]

输出对应的\(1\) ~\(n\) 的排列

\(1 \leq k \leq 50000\)

还是设当前第 \(i\) 位为 \(x\)，则 \(S_i=x-1-cnt\)

考虑把所有数加入集合，每次把用到的数删掉，每次求当前数是什么，等价于在这个集合中求区间第 \(k\) 大

即我们要维护的是 删除+区间第 \(k\) 大

考虑平衡树，也可以整体二分

#include<bits/stdc++.h>
#include<ext/rope>
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x]) //注意加了&
using namespace std;
using namespace __gnu_cxx;

const int N=5e4+10;
int n;
int b[N];
rope<int> a;

void solve()
{
	n=fr();
	b[0]=1;
	for(int i=1;i<=n;i++) b[i]=i;
	b[n+1]=0; //rope到0停止 注意清空
	a=rope<int>(b);
	
	for(int i=1;i<=n;i++)
	{
		int x=fr();
		int now=a[x+1];
		fw(now);
		if(i!=n) pt;
		a.erase(x+1,1);
	}
	nl;
}

int main()
{
	int T=fr();
	while(T--) solve();
	
	return 0;
}

---

P3014 [USACO11FEB]Cow Line S

如何从排名恢复序列？

我们考虑原来的过程，首先将排名--，就是比它小的排列数

每次除 \((n-i)!\) 得到的系数就是当前剩余数中比它小的数，然后剩下的 \(order\) 就是它的余数

const int N=25;
int n,m;
char op[2];
int fac[N],s[N],b[N];
rope<int> a;

void add(int i,int x){for(;i<=n;i+=i&-i) s[i]+=x;}
int query(int i)
{
	int res=0;
	for(;i;i-=i&-i) res+=s[i];
	return res;
}

void per(int id)
{
	b[n+1]=0; //rope到0停止 注意清空
	a=rope<int>(b);
	
	for(int i=1;i<=n;i++)
	{
		int x=id/fac[n-i]; //当前系数
		int now=a[x+1];
		fw(now),pt;
		a.erase(x+1,1);
		id-=x*fac[n-i]; //取余数
	}
	nl;
	b[n+1]=n+1;
}

void order()
{
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		int x=fr();
		int cnt=query(x-1),rest=n-i;
		ans+=(x-1-cnt)*fac[rest];
		add(x,1);
	}
	fw(ans+1),nl;
	memset(s,0,sizeof s);
}

signed main()
{
	n=fr(),m=fr();
	fac[0]=b[0]=1;
	for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i,b[i]=i;
	while(m--)
	{
		scanf("%s",op);
		if(op[0]=='P') per(fr()-1);
		else order();
	}
	
	return 0;
}

---

P6035 Ryoku 的逆序对

第一问每个 \(-1\) 的地方它的逆序对数可以是 \([0,n-i]\)，一个乘法原理即可，任意一种情况都可以构造

第二问我们让所有 \(-1\) 的点逆序对都为 \(0\) 即可，和区间第 \(k\) 大等价

const int N=1e6+10,Q=1e9+7;
int n;
int b[N],c[N];
rope<int> a;

int main()
{
	n=fr();
	c[0]=1;
	for(int i=1;i<=n;i++) b[i]=fr(),c[i]=i;
	long long ans=1;
	for(int i=1;i<=n;i++)
	{
		if(!(~b[i])) ans=ans*(n-i+1)%Q;
		else if(b[i]>n-i) {puts("0");return 0;}
	}
	printf("%lld\n",ans);
	
	a=rope<int>(c);
	for(int i=1;i<=n;i++)
	{
		int x;
		if(~b[i]) x=b[i]+1;
		else x=1;
		fw(a[x]),pt;
		a.erase(x,1);
	}
	return 0;
}