Problem Set(CF)
Problem Set(CF)
收录CF好题
T1 Aroma's Search
显然模拟是不行的 根据数据范围应该是直接计算
点的范围是极大的,估计只能走到一小部分点
哪怕纵坐标一直不变,极限情况下也就是 \(\log _a^t\)
而 \(\log _{2}^{10^{16}}\) 大约 \(50\) 个
图片来自题解 https://www.luogu.com.cn/blog/syksykCCC/solution-cf1292b
贪心从左向右选择 (当然自己在点上肯定要的)
假设先选离自己最近的点 Q
极限情况下 \(a_x=2\,b_x=0\,a_y=1\,b_y=0\)
\(dis(Q,Q+1)=(a_x \times x_i + b_x)-a_x=a_x = dis (Q,0)=a_x\)
极端情况下才相等
所以只要向右跑一定不如向左跑
直接枚举每个向左跑的点和第一个向右跑的点(可能没有)
因为不知道从哪个点开始向左最优,也可能直接向右就拿一个最优
134数据有点绝
\(code\)
#include<bits/stdc++.h>
#define int long long
#define pt putchar
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x])
using namespace std;
const int N=66;
int ax,ay,bx,by,xs,ys,t,n,ans;
int x[N],y[N];
int fr(){
int x=0,flag=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
return x*flag;
}
void fw(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) fw(x/10);
putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
int dis(int a,int b,int c,int d) {return llabs(a-b)+llabs(c-d);}
void init()
{
for(int i=2;;i++)
{
x[i]=ax*x[i-1]+bx;
y[i]=ay*y[i-1]+by;
if(x[i]>xs && y[i]>ys && dis(xs,x[i],ys,y[i])>t)
{
n=i;
break;
}
}
}
signed main()
{
x[1]=fr(),y[1]=fr(),ax=fr(),ay=fr(),bx=fr(),by=fr();
xs=fr(),ys=fr(),t=fr();
init();
for(int i=1;i<=n;i++)
{
int val=dis(xs,x[i],ys,y[i]),cnt=1; //自己
int nowx=x[i],nowy=y[i];
if(val>t) continue;
if(i>1) //turn left
{
for(int j=i-1;j;j--)
{
val+=dis(nowx,x[j],nowy,y[j]);
if(val>t) break;
cnt++;
nowx=x[j],nowy=y[j];
}
}
if(val<t) //turn right
{
for(int j=i+1;j<=n;j++)
{
val+=dis(nowx,x[j],nowy,y[j]);
if(val>t) break;
cnt++;
nowx=x[j],nowy=y[j];
}
}
ans=max(ans,cnt);
}
fw(ans);
return 0;
}
T2 Ehab the Xorcist
构造题
这里用的技巧也是先假设答案序列
性质1 : \(sum(xor) \leq sum(add)\)
\(val(xor_{a_i}) \leq val(a_i)\)
很好理解 原来 \(sum\) 与当前数二进制某一位重复了,则该位贡献没有
\(xor\) 就是不完全加法
性质2 \(sum(xor)\) 与 \(sum(add\)) 奇偶性相同
序列 \(x\) 个奇数 \(x\) 为奇 \(sum(xor)\) 也为奇 \(sum(add)\) 同理
为偶同理
所以无解为上述情况
如何构造?
当 \(u == v\) 直接特判即可
显然的 \(sum(xor)\) 不太好构造
那么干脆直接放个 \(u\) 上去 剩下两两配对 \(xor\) 完直接为0
反正 \(u \lt v\)
这样就保证了 \(sum(xor)\) 接下来保证 \(sum(add)\)
剩下的 \(xor\) 起来为0,为了使序列最短,就整两个就行了
那么这样 就构造成功了 \(n=3\) 的情况
\(w[i]=[a=u,b=(v-u)/2,c=(v-u).2]\)
其实应该从 \(\frac{(v-u)}{2}\) 如果 \(v\;mod\;2\,!=\,u\;mod\;2\) 构造不合理来推断无解情况的
特判下 组合的情况 因为这个时候 \(u,v\) 都保证了可以尝试缩成2
#include<bits/stdc++.h>
#define int long long
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x])
using namespace std;
const int N=5e6+10;
int u,v;
int fr(){
int x=0,flag=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
return x*flag;
}
void fw(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) fw(x/10);
putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
signed main()
{
u=fr(),v=fr();
if(!u && !v) puts("0");
else if(u>v || (u&1)!=(v&1)) puts("-1");
else if(u==v) puts("1"),fw(u);
else
{
int a=u,b=(v-u)/2,c=(v-u)/2;
if((a^(b+c))==u)
{
puts("2");
fw(a),pt,fw(b+c);
}
else if(((a+b)^c)==u)
{
puts("2");
fw(a+b),pt,fw(c);
}
else
{
puts("3");
fw(a),pt,fw(b),pt,fw(c);
}
}
return 0;
}
T3 Absolute Sorting
题目给了一个 \(x\) 的大致范围,暴力的话直接枚举肯定超时
想办法把这个区间缩小一下,直到枚举不会超时
考虑最终的序列,只用保证相邻两项单调不减即可 即 \(|a_i-x| \leq |a_{i+1}-x|\)
-
\(a_i \lt a_{i+1}\)
\(0 \leq x \leq \lfloor \frac{a_i+a_{i+1}}{2} \rfloor\)
-
\(a_i \gt a_{i+1}\)
\(\lceil \frac{a_i+a_{i+1}}{2} \rceil \leq x\)
-
\(a_i == a_{i+1}\)
\(0 \to + \infty\)
不断缩小边界 \(l\) \(r\) 求得一解
注意上取整不要用ceil 用+1的形式
max(c,ceil((a+b)/2) -> max(c,(a+b+1)/2)
复杂度 \(O(n)\)
\(code\)
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+10;
int t,n;
int a[N];
int fr(){
int x=0,flag=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
return x*flag;
}
void fw(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) fw(x/10);
putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
int solve(int l,int r)
{
for(int i=1;i<n;i++)
{
if(a[i]==a[i+1]) continue;
if(a[i]<a[i+1]) r=min(r,(a[i]+a[i+1])/2);
else l=max(l,(a[i]+a[i+1]+1)/2);
}
return (l<=r)?l:-1;
}
signed main()
{
t=fr();
while(t--)
{
n=fr();
for(int i=1;i<=n;i++) a[i]=fr();
fw(solve(0,1e9)),puts("");
}
return 0;
}
T4 Permutation Game
一眼 贪心 or 数学
注意:两个人不会将所有的数染色,只会染那些位置错误的数。
肯定不能模拟,所以需要计算一个什么来直接判断
定义
\(p1:a_i ==i\,\,and\,\,a_i\not= n-i+1\)
\(p2:a_i==n-i+1\,\,and\,\,a_i\not=i\)
\(p3:a_i\not=i\,\,and\,\,a_i \not= n-i+1\)
这里注意 \(p1\,\,and\,\,p2\) 需要同时满足两项,才需要染色
刚开始只能染色,先手显然先染色 \(p2\) 染色 \(p1\) 是傻了 染色 \(p3\) 给后手坐享其成
同样后手先染色 \(p1\)
染完 \(p1\,p2\) 接着染色 \(p3\)
如果中途哪个抽风排列,另一个人可以直接换回来
等价于没变
如果 \(p2+p3 \leq p1\) 先手赢
如果 \(p1+p3 \lt p2\) 后手赢
剩下的两个人可以靠反复拉扯变成平局
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int n,t,p1,p2,p3,x;
int fr(){
int x=0,flag=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
return x*flag;
}
void fw(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) fw(x/10);
putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
int main()
{
t=fr();
while(t--)
{
n=fr();
p1=p2=p3=0;
for(int i=1;i<=n;i++)
{
x=fr();
p1+=(x==i && x!=n-i+1);
p2+=(x==n-i+1 && x!=i);
p3+=(x!=i && x!=n-i+1);
}
if(p2+p3<=p1) puts("First");
else if(p1+p3<p2) puts("Second");
else puts("Tie");
}
return 0;
}
T5 Yet Another Tournament
题面非常难懂
建议看下题解的题目大意 link
对于这种没有思路的题,先假设答案,观察性质,反推思路即可
考虑自己第 \(k\) 名
原来的 \(i\) 选手 最多排名 \(-1\) ,当且仅当 \(i+1\) 选手输了
排到第 \(k\)
-
赢 \(n-k+1\) 场 即使不打 \(n-k\) 也能排到第 \(k\) 名
-
赢 \(n-k\) 场 但是必须打赢 \(n-k+1\)
eg:要第一名 赢 \(n\) 场 或者 赢 \(n-1\) 场 但是必须赢 \(n\)
至于剩下的人 排名高的你大不到,排名低的威胁不到你
发现具有二分性 考虑二分答案
另外, 把 \(a_i\) 从小到大排序 贪心选择
2的情况细分
- 如果原最小组合包含了 \(n-k+1\) 成立
- 贪心选择原最小组合中最大的 \(a_i\) 与 \(a_{n-k+1}\) 交换 看强选是否成功
\(code\)
#include<bits/stdc++.h>
#define int long long
#define pi pair<int,int>
#define val first
#define id second
using namespace std;
const int N=5e5+10;
int n,m,t;
pi w[N];
int to[N],s[N];
int fr(){
int x=0,flag=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
return x*flag;
}
void fw(int x){
if(x>9) fw(x/10);
putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
bool check(int mid)
{
if(s[n-mid+1]<=m) return 1; //情况1
if(s[n-mid]<=m && to[n-mid+1]<=n-mid) return 1; //情况2.1 最小的组合包含n-mid
if(s[n-mid]<=m && (mid==n?0:s[n-mid-1])<=m-w[to[n-mid+1]].val) return 1; //情况2.2 强选
return 0;
}
signed main()
{
t=fr();
while(t--)
{
n=fr(),m=fr();
for(int i=1;i<=n;i++)
w[i]={fr(),i};
sort(w+1,w+1+n);
for(int i=1;i<=n;i++)
{
s[i]=s[i-1]+w[i].val;
to[w[i].id]=i;
}
int l=1,r=n+1,ans=n+1;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1,ans=mid;
else l=mid+1;
}
fw(ans),puts("");
}
return 0;
}
T6 Different Arrays
多段转移 \(\to\) dp
口胡容斥一下 不重复就是 \(2^{n-2}\)
口胡性质 :在进行第 \(i\) 次操作时,当\(a_{i+1} \not= 0\) 时产生两次贡献,为0时加减等价产生一次贡献。
因为每次操作转移的时候只会影响 \(a_{i+2}\) 和 \(a_i\)
对后面的影响仅在 \(a_{i+2}\)
划分集合:
每一种操作序列 按照操作数为 \(i-2\) 时,第 \(i+1\) 位的值划分集合。
\(f[i][j]\) 指针为 \(i-1\),序列 \(a_{i+1}\) 位为 \(j\)
此时 \(a_{i+1}\) 相对 \(i-1\) 为 \(i+2\)
每次递归必然为搜索树中的一种,复杂度为 \(O(nT)\)
\(T\) 为搜索的值域
大概为 \(-300 \times 300 \to 300 \times 300\)
注意值域可能为负数,加上数组偏移量 \(S\)
\(code\)
#include<bits/stdc++.h>
using namespace std;
const int N=310,Q=998244353,S=90005;
int n;
int w[N],f[N][2*N*N];
int fr(){
int x=0,flag=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
return x*flag;
}
void fw(int x){
if(x>9) fw(x/10);
putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
int dfs(int now,int val) //当前指针为 now-1 当前 a(now)==val a(now-1+2)+-a(now)
{
if(now==n) return 1; //进行了 n-2 次操作
if(~f[now][val+S]) return f[now][val+S]; //记忆化
return f[now][val+S]=(dfs(now+1,w[now+1]+val)%Q+(val!=0)*dfs(now+1,w[now+1]-val)%Q)%Q;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) w[i]=fr();
memset(f,-1,sizeof f);
cout<<dfs(2,w[2]); //未进行一次操作 当前i=1 a(i+1)=a2
return 0;
}
T7 Doremy's Experimental Tree
容斥+最小生成树
源自大佬思路 https://zhuanlan.zhihu.com/p/587885558
题意
-
给定一棵树带权树
-
定义一种操作为任取两个树上的点 用长度为1的边连接
-
给出所有点到环上距离自己最小的点的距离之和
-
假设两点为\(i\;j\) 则距离和 \(d\) 记为 \(f(i,j)\)
-
给定所有 \(f(i,j)\) 还原出整棵树
性质1
从 \(f(x,x)\)入手 显然是剩下树上点到自己的最短路。
如何求两点间的距离 考虑每一条边的贡献。
任取树上两个点 \(u\;v\)
图中数字为每条边被在最短路上的次数。
下为大佬图片 已授权。
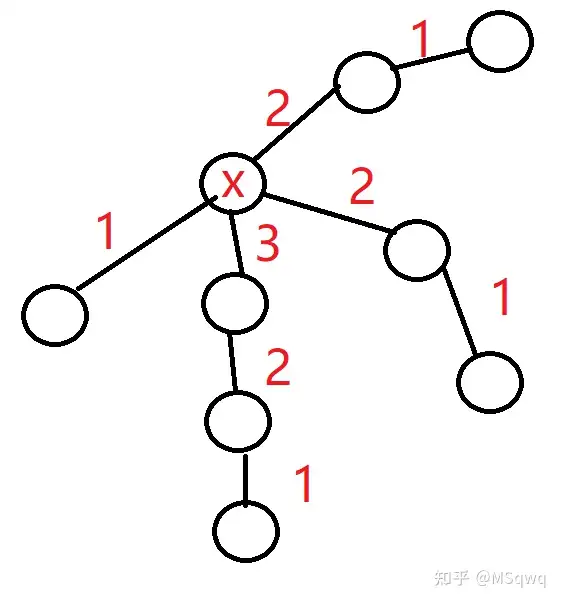
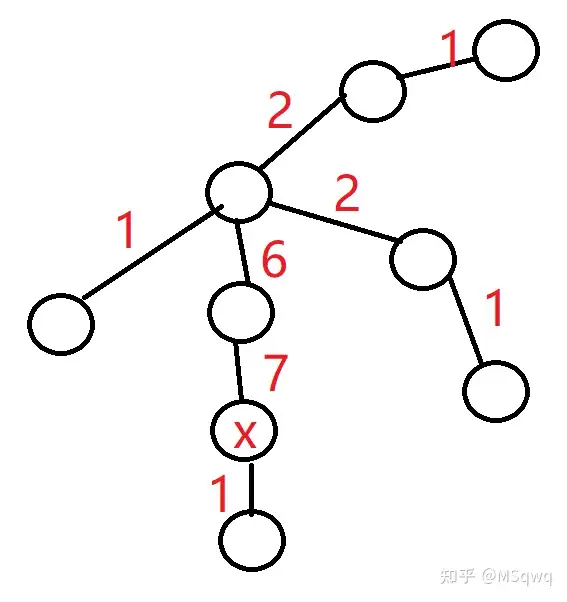
性质2
所有环之外的点 到达 \(u\;v\) 的边提供的贡献相同。
比如最右上角的那条边 两个x的情况 都只被算了一遍。
性质3
\(d(u,u)+d(v,v)\) 和中 环内的每条边被计算 \(n\) 次。
上图两个 \(x\) 之间 \(6+3=2+7=9=n\)
形象理解 记第一个图中 \(x\) 为 \(u\) 第二个中 \(x\) 为 \(v\),\(u\;v\) 中间的点为 \(c\)
\(u\) 上面 \(v\) 下面 数量相同。
这里算的时 \(d(u,u)+d(v,v)\) 每条边总和被遍历次数 下同。
\(u \to c\) 第一个图中 这条边被 \(c\) 下面(含 \(c\) ) 每个点加一次。
\(c \to u\) 第二个图中 这条边被 \(u\) 上面(含 \(u\) ) 每个点加一次。
\(c\) 下面的点,\(u\) 上面的点 \(+\,u + c =n\)
得证。
环之外的点产生的边权贡献全部减掉。
即 \(edge(u,v)\) = \(\frac{f(u,u)+f(v,v)-2 \times f(u,v)}{n}\)
跑最小生成树 去掉无用边。
证明 一条无用边 \(u \to v\) 且 \(u \to i \to ... \to j \to v\)
即 \(u\;v\) 之间至少有一个点。
那么按照 kru 算法 排序后 \(u \to i\),\(i \to ...\;j \to v\) 的边一定先被选 。
轮到 \(u \to v\) 这条边时已经联通。
得证。
流程
1 预处理任意两点距离
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i!=j) ed[++m]={i,j,(f[i][i]+f[j][j]-2*f[i][j])/n};
2 kru 最小生成树
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2010;
int n,m;
int p[N];
ll f[N][N];
struct node{
int u,v;
ll w;
bool operator<(const node&Q)const
{
return w<Q.w;
}
}ed[N*N];
ll fr()
{
ll x=0;
char ch=getchar();
while(ch<'0' || ch>'9') ch=getchar();
while(ch>='0' && ch<='9')
{
x=x*10+(ch-'0');
ch=getchar();
}
return x;
}
int find(int x)
{
if(x!=p[x]) p[x]=find(p[x]);
return p[x];
}
void kru()
{
for(int i=1;i<=n;i++) p[i]=i;
sort(ed+1,ed+1+m);
int cnt=0;
for(int i=1;i<=m;i++)
{
int a=ed[i].u,b=ed[i].v;
ll c=ed[i].w;
int pa=find(a),pb=find(b);
if(pa!=pb)
{
p[pa]=pb;
cnt++;
printf("%d %d %lld\n",a,b,c);
}
if(cnt==n-1) break;
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
f[i][j]=f[j][i]=fr();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
ed[++m]={i,j,(f[i][i]+f[j][j]-2*f[i][j])/n};
kru();
return 0;
}
T8 All Possible Digits
左侧为最高位,右侧为最低位 \(2 \leq p \leq 1e9\)
\(p=5 \; \;a=[2,3,4]\;\;x=2 \times 5^2 +3 \times 5^1+4 \times 5^0\)
虽然 \(p\) 很大,但是操作只有 \(+1\) 一种!
考虑最低位贡献 \(a[1] \to p-1\)
剩下的贡献就是 \(a[i]\) 本身
一旦 \(a[0]\) 进位,可以产生 \(0 \to p-1\) 的贡献
找到最右侧最左侧空缺点,然后分类讨论下就行了
注意 \(a[1]\) 会变,要先记下来
\(code\)
#include<bits/stdc++.h>
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x])
using namespace std;
const int N=110;
int n,t,p;
int a[N];
unordered_set<int> s;
int fr(){
int x=0,flag=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
return x*flag;
}
void fw(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) fw(x/10);
putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
void solve()
{
s.clear();
memset(a,0,sizeof a);
n=fr(),p=fr();
for(int i=n;i;i--)
a[i]=fr(),s.insert(a[i]);
if(s.size()==p) {puts("0");return;}
int l=0,r=p-1;
while(s.count(l)) l++;
while(s.count(r)) r--;
if(a[1]<l) {fw(r-a[1]),nl;return;} //不进位
int t=a[1];
for(int i=1;i<=n;i++) //进位
{
a[i]=0,a[i+1]++;
if(a[i+1]!=p) break;
}
for(int i=1;i<=n;i++) s.insert(a[i]);
if(a[n+1]) s.insert(a[n+1]); //特判下全进位情况
a[1]=t,l=a[1]-1;
while(s.count(l)) l--;
fw(p-a[1]+max(l,0)),nl;
}
signed main()
{
t=fr();
while(t--) solve();
return 0;
}
T9 Restore the Permutation
首先根据样例推测,偶数位放 \(b[i]\)
然后考虑基数位
为了保证字典序最小,可以贪心的从后往前放,这样无后效性,方便了很多
这样构造有一个显然的无解,就是 \(b\) 数组有重复的数
把 \(b\) 数组的数放完之后,剩下的数存到一个 \(set\) 里面去
每次二分找恰好 \(\leq\) 自己的数,给前面留更多空间,避免了前面选了小数字,后面放不了的情况
当然这里也有一个无解情况,因为后面是时刻最优,当匹配不了的时刻就是无解
\(code\)
#include<bits/stdc++.h>
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define val first
#define id second
#define pb push_back
#define go(it) for(auto &it:as[x]) //注意加了&
using namespace std;
const int N=2e5+10;
int n,t;
int p[N],b[N];
unordered_set<int> s;
set<int> rest;
int fr(){ //double 不能快读!!!!
int x=0,flag=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
return x*flag;
}
void fw(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) fw(x/10);
putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
void solve()
{
n=fr();s.clear();rest.clear();
for(int i=1;i<=(n>>1);i++) b[i]=fr();
for(int i=1;i<=n;i++) p[i]=0;
//首先保证max 偶数位放原数
for(int i=2;i<=n;i+=2)
{
if(!s.count(b[i/2]))
{
p[i]=b[i/2];
s.insert(p[i]);
}
else {puts("-1");return;} //无解1
}
//基数位贪心放
for(int i=1;i<=n;i++)
if(!s.count(i)) rest.insert(i);
for(int i=n-1;i>=1;i-=2)
{
auto it=rest.lower_bound(p[i+1]);
if(it==rest.begin()) {puts("-1");return;} //无解2
it--;
p[i]=*it;
rest.erase(it);
}
for(int i=1;i<=n;i++) fw(p[i]),pt;
nl;
}
int main()
{
t=fr();
while(t--) solve();
return 0;
}
T10 Air Conditionern
维护温度值域,每次求交集即可,类似之前缩范围的一个题
\(init:L=R=m\)
\(L-=t_{i+1}-t_i\;R+=t_{i+1}-t_i\)
\(R=min(R,r_i)\;L=max(L,l_i)\)
这样保证了每次都满足要求
T11 a-Good String
首先 \(2^k\) 考虑分治
要想直接变这个字符串有点困难
为什么不枚举所有情况,然后直接和原串对比,看看需要该多少呢
发现一个很好的性质 每次递归减半 \(O(nlogn)\)
直接爆搜,然后决策把那一边变成 \(aaaa\) 这种形式,再加个最优性剪枝就行了
void dfs(int l,int r,char now,int cnt)
{
if(cnt>=ans) return;
if(l==r) {ans=min(ans,cnt+(s[l]!=now));return;}
int cnt1=0,cnt2=0,mid=(l+r)>>1;
for(int i=l;i<=mid;i++) cnt1+=(s[i]!=now);
for(int i=mid+1;i<=r;i++) cnt2+=(s[i]!=now);
dfs(l,mid,now+1,cnt2+cnt),dfs(mid+1,r,now+1,cnt1+cnt);
}
T12 Edge Weight Assignment
所有叶子节点到根路径的异或值相同
先设置一个度不为 \(1\) 的点为根,方便考虑
首先明显两个问题
最少值
根据样例,不是 \(1\),就是 \(3\)
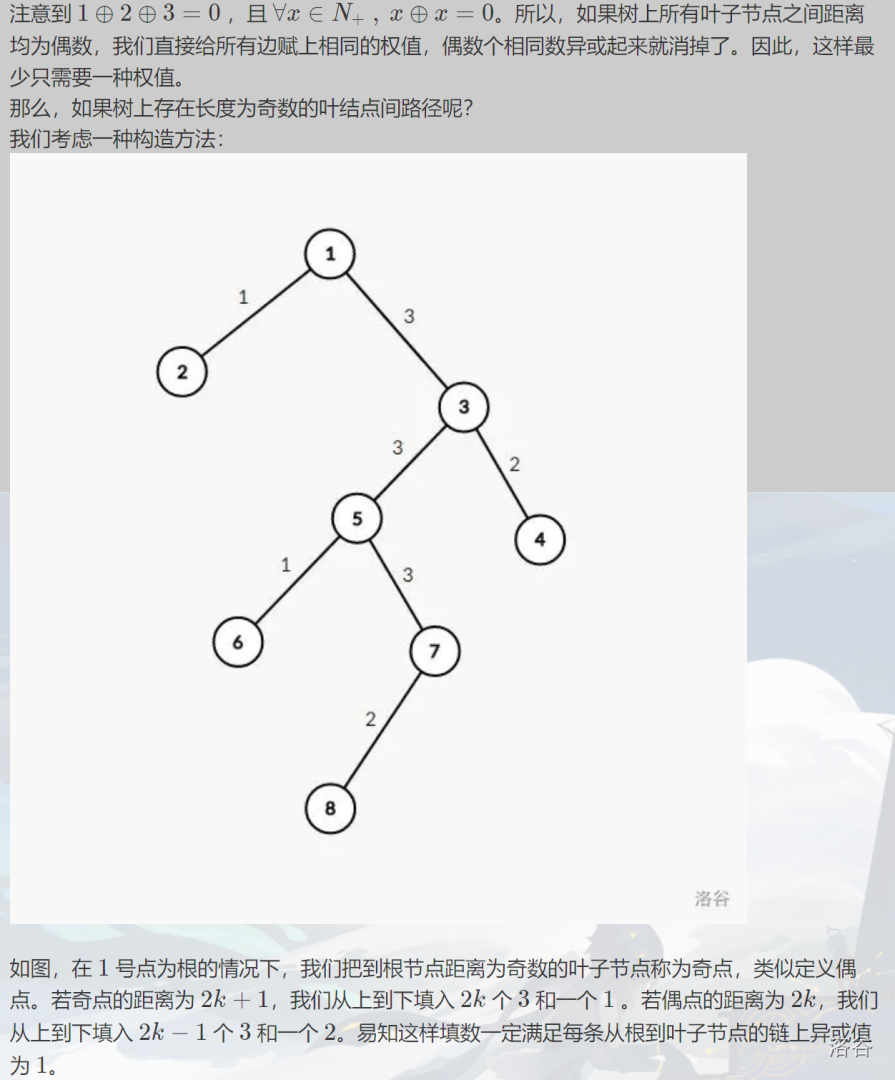
最大值 \(dp\) 口胡容斥下
首先,极致贪心,每条边都不一样,然后考虑哪些情况必须边权相等.
到了倒数第二层的节点,所有儿子都是叶子节点,就一条边,必须相等
因为边权是任意的,所以可以构造一种方案使剩下的边都不相同,每个叶子节点到根节点异或和为 \(0\)
\(ans=\Sigma edge - \Sigma (cnt_x-1)\;\;[\,\forall\;son_x=leaf]\)
#include<bits/stdc++.h>
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x])
using namespace std;
const int N=1e5+10;
int n,u,v,g;
int f[N];
vector<int> as[N];
vector<int> leaf;
int fr(){
int x=0,flag=1;
char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=x*10+(ch-'0');
ch=getchar();
}
return x*flag;
}
void fw(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) fw(x/10);
putchar(x%10+'0');
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
void dfs(int x,int rt,int dep)
{
if(as[x].size()==1)
{
f[rt]++;
leaf.pb(dep),g=dep&1;
return;
}
go(it) if(it!=rt) dfs(it,x,dep+1);
}
int main()
{
n=fr();
for(int i=1;i<n;i++)
{
u=fr(),v=fr();
as[u].pb(v);
as[v].pb(u);
}
for(int i=1;i<=n;i++)
if(as[i].size()!=1) {dfs(i,-1,0);break;}
int res=1,ans=n-1;
for(auto it:leaf) if(g!=(it&1)) {res=3;break;}
fw(res),pt;
for(int i=1;i<=n;i++) if(f[i]) ans-=f[i]-1;
fw(ans);
return 0;
}
T13 Sad powers
首先 \(p \geq 3\) 的直接算就可以了
然后 \(p==2\) 本来是 \(sqrtl(n)\) 但是 \(p \geq 3\) 的中的还有平方数,会重复
那么就把 \(x=a^p (p \geq 3)\;and\;x=b^2\) 的数容斥去掉就可以了
\(l,r\) 就前缀和一下就行了
#include<bits/stdc++.h>
#define int long long
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x]) //注意加了&
using namespace std;
const int N=1e18;
int n,q,cnt;
vector<int> as;
int fr() //double不能快读
{
int x=0,flag=1;
char ch=getchar();
while(ch<'0' || ch>'9')
{
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
{
x=x*10+(ch-'0');
ch=getchar();
}
return x*flag;
}
void fw(int x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) fw(x/10);
putchar(x%10+'0');
}
int calc(int x)
{
return sqrtl(x)+(upper_bound(as.begin(),as.begin()+cnt,x)-as.begin());
//upper找的就是这个数下标从0开始 0 1 2 3 4 5 比如下标是5 前面就是有5个数
}
signed main()
{
for(int i=2;i*i*i<=N;i++)
{
int x=i*i;
while(x<=N/i)
{
x*=i;
int t=sqrtl(x);
if(abs(t*t-x)>1e-8) as.pb(x); //平方数去掉
}
}
sort(as.begin(),as.end());
cnt=unique(as.begin(),as.end())-as.begin(); //排序去重下
q=fr();
for(int i=1;i<=q;i++)
{
int l=fr(),r=fr();
fw(calc(r)-calc(l-1)),nl;
}
return 0;
}
T14 Binary Cards
\(n\ leq 40\) 我们考虑如何省去一半然后搜索解决
首先每个 \(2^k\) 最多选一次,否则不如 \(2^{k+1}\)
\(2^k\) 和 \(-2^k\) 等价于 \(-2^k\) 和 \(2^{k+1}\),没必要同时选 \(2^k\) 和 \(-2^k\)
按二进制位考虑,有 \(1\) 必选 \(2^k\) 或者 \(-2^k\) 搜索即可,相当于用个 \(1\) 消去这些
没有 \(1\) 必不选,直接到下一层去,这样一定可以保证所有数全部消干净
每层都去重,因为二进制位的减少,每层的不同类数都在减少
\(O(n\log w)\)
const int N=1e5+10,M=19;
int n;
vector<int> num;
vector<int> dfs(int dep)
{
if(dep>20) return vector<int>(0); //返回一个 size=0 的vector
sort(num.begin(),num.end());
auto it=unique(num.begin(),num.end()); //返回第一个重复元素的下标
num.erase(it,num.end()); //前闭后开
bool fl=0;
for(auto v:num) fl|=v&1;
if(!fl)
{
for(auto &v:num) v>>=1; //注意要用 & !!! 否则 num 里面还是没变
return dfs(dep+1);
}
vector<int> base=num;
num.clear();
for(auto v:base)
{
if(v&1) num.pb((v-1)>>1); //选正的凑
else num.pb(v>>1); //没有 1 不用凑
}
vector<int> ans1=dfs(dep+1);
ans1.pb(1<<dep);
num.clear();
for(auto v:base)
{
if(v&1) num.pb((v+1)>>1); //选负的相当于接下来需要消去 2^{k+1} 就进到上一位
else num.pb(v>>1);
}
vector<int> ans2=dfs(dep+1);
ans2.pb(-(1<<dep));
return (ans1.size()<ans2.size())?ans1:ans2;
}
int main()
{
n=fr();
for(int i=1;i<=n;i++) num.pb(fr());
vector<int> ans=dfs(0);
fw(ans.size()),nl;
for(auto v:ans) fw(v),pt;
return 0;
}
T15 Rest In The Shades
考虑任意 \(AB\) 上一点和所求点的连线,设改点为 \(C\),连起来就是三角形 \(ABC\)
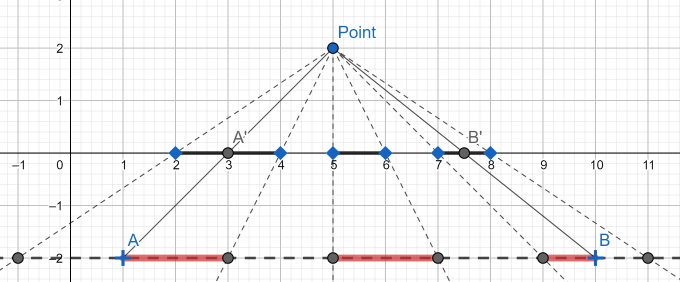
设连线交点 \(A'\;B'\) 我们预处理 \(A'\) \(B'\) 中间这些,如图就是 \([5,6]\)(前缀和预处理即可),然后二分 \(A'\) 所在线段处理这个不整段
再根据相似三角形找出来这些 \(x\) 轴上的投影
const int N=2e5+10;
int n,xa,xb,sy,q;
double s[N],segl[N],segr[N];
set<pair<double,int>> dot;
double calc(int l,int r){return (r>=l)?(s[r]-s[l-1]):0.0;}
signed main()
{
sy=fr(),xa=fr(),xb=fr(),n=fr();
for(int i=1;i<=n;i++)
{
scanf("%lf%lf",&segl[i],&segr[i]);
s[i]=s[i-1]+segr[i]-segl[i];
dot.insert({1.0*segl[i],i}),dot.insert({1.0*segr[i],i});
}
q=fr();
while(q--)
{
int x=fr(),y=fr();
double len1=1.0*y/(y-sy)*fabs(x-xa);
double l=(x<xa)?(x+len1):(x-len1);
double len2=1.0*y/(y-sy)*fabs(x-xb);
double r=(x<xb)?(x+len2):(x-len2);
auto it1=dot.lower_bound({l,0});
auto it2=dot.lower_bound({r,0});
if(it1==dot.end())
{
puts("0.0000000000"); //注意输出
continue;
}
int L=it1->second;
if(it2==dot.end()) it2--,r=segr[n];
int R=it2->second;
double val=0;
if(L==R)
{
if(r>segl[L] && l>=segl[L]) val=r-l;
else if(l<segl[L] && r>=segl[L]) val=r-segl[L];
else val=0;
}
else val=segr[L]-max(l,segl[L])+max(0.0,r-segl[R]);
double ans=calc(L+1,R-1)+val;
ans*=1.0*(y-sy)/y;
printf("%.10lf\n",ans);
}
return 0;
}
T16 Rain of Fire
首先二分答案 \(x\)
考虑直接 \(O(n^2)\) 建边,然后 \(dsu\) 判联通性
分类讨论一下,新加一个点,如果在那种十字路口的话,可以最多连接 \(4\) 个连通块,设连通块个数为 \(cnt\),新点为 \(now\)
\(cnt==1\) \(ok\)
\(cnt==2\)
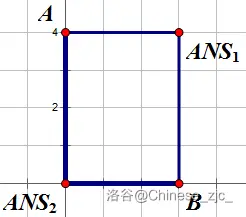
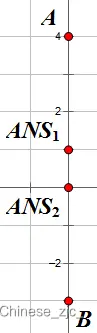
\(cnt==3\)
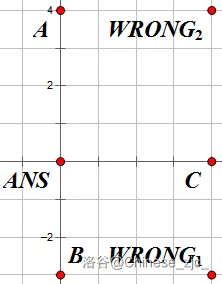
\(cnt==4\)
考虑新增点,只要该位置可以和某个连通块联通,等价于拥有了这个连通块的"颜色",一个点拥有的颜色多少就可以判断能联通几个连通块
因为这个新点的位置坐标肯定是由两个原来的点控制的,我们再次 \(O(n^2)\) 枚举出新点即可
\(cnt \leq 2\) 直接枚举即可
\(3\leq cnt \leq 4\) 时
用 \(g_{i,j}\) 表示 \(i\) 号连通块和 \(j\) 号连通块联通,然后给它一个编号,到时候 \(1<<id\) 就代表
考虑到不同的 \(x\) 和 \(y\) 分别都只有 \(n\) 种,我们直接离散化,这样就可以开下一个 \(n \times n\) 的数组,把每个点作为新点能拥有几种"颜色"记下来
const int N=1e3+10;
int n;
int x[N],y[N],p[N],col[N],link[N][N];
struct node{int x,y;}dot[N];
const int g[5][5]={ //状压数组
{0,0,0,0,0},
{0,0,1,2,3},
{0,1,0,4,5},
{0,2,4,0,6},
{0,3,5,6,0}
};
int find(int x)
{
if(x!=p[x]) p[x]=find(p[x]);
return p[x];
}
int count(int x)
{
int res=0;
while(x) x-=x&(-x),res++;
return res;
}
bool check(int T)
{
for(int i=1;i<=n;i++) p[i]=i,col[i]=0; //连通块编号
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
if(find(i)!=find(j))
{
if(dot[i].x==dot[j].x && abs(y[dot[i].y]-y[dot[j].y])<=T) p[find(i)]=find(j);
else if(dot[i].y==dot[j].y && abs(x[dot[i].x]-x[dot[j].x])<=T) p[find(i)]=find(j);
}
int cnt=0;
for(int i=1;i<=n;i++)
if(!col[find(i)]) col[find(i)]=++cnt;
if(cnt==1) return 1;
else if(cnt==2)
{
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
if(find(i)!=find(j))
{
if(dot[i].x==dot[j].x && abs(y[dot[i].y]-y[dot[j].y])<=(T<<1)) return 1;
else if(dot[i].y==dot[j].y && abs(x[dot[i].x]-x[dot[j].x])<=(T<<1)) return 1;
else if(abs(x[dot[i].x]-x[dot[j].x])<=T && abs(y[dot[i].y]-y[dot[j].y])<=T) return 1;
}
}
else if(cnt==3 || cnt==4)
{
memset(link,0,sizeof link);
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
if(find(i)!=find(j) && abs(x[dot[i].x]-x[dot[j].x])<=T && abs(y[dot[i].y]-y[dot[j].y])<=T)
{
link[dot[i].x][dot[j].y]|=1<<g[col[find(i)]][col[find(j)]];
link[dot[j].x][dot[i].y]|=1<<g[col[find(i)]][col[find(j)]];
}
if(cnt==3)
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(count(link[i][j])>=2) return 1;
}
else
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(count(link[i][j])>=4) return 1;
}
}
return 0;
}
signed main()
{
n=fr();
for(int i=1;i<=n;i++) x[i]=dot[i].x=fr(),y[i]=dot[i].y=fr();
sort(x+1,x+1+n),sort(y+1,y+1+n);
for(int i=1;i<=n;i++)
{
dot[i].x=lower_bound(x+1,x+1+n,dot[i].x)-x;
dot[i].y=lower_bound(y+1,y+1+n,dot[i].y)-y;
}
int l=1,r=1e18,ans=INT_MAX;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)) r=mid-1,ans=mid;
else l=mid+1;
}
if(ans!=INT_MAX) fw(ans);
else puts("-1");
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号