Problem Set(main)
Problem Set(main)
收录主题库内好题
T1 P8956 CGOI-3 招魂术
数学
打表发现 大概50个左右后,\(F_{X,Y}(i)\) 与 $ F_{X,Y}(i-2)$ 的差值为1
类似 \(3\;3\;4\;4\;5\;5\)
即 \(x \,\, x \,\to x+1\,\,x+1 \to x+2\,\,x+2 ....\)
非循环节部分直接暴力算即可,后面直接快速幂
判断错位情况
发现相隔一个的差值相同:
\(3\;3\;4\;4\;5\;5\)
\(7\;7\;8\;8\;9\;9\)
\(11\;12\;12\;13\;13\;14\)
分开算两个间隔的贡献即可
\(code\)
const int Q=998244353;
int t,n,a,b,x,y;
int qkw(int a,int k)
{
int ans=1,base=a;
while(k)
{
if(k&1) ans=ans*base%Q;
base=base*base%Q;
k>>=1;
}
return ans;
}
signed main()
{
cin>>t;
while(t--)
{
n=fr(),a=fr(),b=fr(),x=fr(),y=fr();
if(n==1) fw(((x-a)%Q+Q)%Q),nl;
else
{
int ans=(x-a)*(y-b)%Q;
for(int i=3;i<=min((ll)100,n);i++)
{
int c=(ll)sqrtl(a*b)+1,z=(ll)sqrtl(x*y)+1;
ans=ans*(z-c)%Q;
a=b,b=c,x=y,y=z;
}
if(n<=100) fw((ans%Q+Q)%Q),nl;
else
{
n-=100;
ans=ans*qkw(x-a,(n-1)/2+1)%Q;
ans=ans*qkw(y-b,(n-2)/2+1)%Q;
fw((ans%Q+Q)%Q),nl;
}
}
}
return 0;
}
T2 P8957 CGOI-3 巫泡弹弹乐
kru+优化建边 贪心
核心思想 \(edge(a \to c) > edge(a \to b) +edge(b \to c)\)
显然 \(edge(a \to c)\) 无需存在
先把每个点按 \(a\) 排序,每个点和前面最小的 \(b\) 的点连边
然后同理按 \(b\) 排序
这样首先保证了连通性,每个点必然向之前的点连了边
第一种情况保证了 \(a\) 连别的都没用
反证: \(edge(i,elsei(\not=mina))\)
用到这条边说明之前不存在更小的边连通这两个点
显然的 \(edge(elsei_{mina},elsei)\) 这里 \(a\) 更小,假设+b了更大
那么按了 \(b\) 排序了之后又在后面还是连了边
成立
贪心证明不了
注意排序之后就不是原来的编号了,还要记录一个 \(id\)
\(code\)
const int N=2e6+10;
int n,m;
int p[N];
struct path{
int u,v,w;
}ed[N];
struct query{
int a,b,id;
}q[N],ans[N];
bool cop(path a,path b) {return a.w<b.w;}
bool copa(query x,query y) {return x.a<y.a;}
bool copb(query x,query y) {return x.b<y.b;}
int find(int x)
{
if(x!=p[x]) p[x]=find(p[x]);
return p[x];
}
void kru()
{
sort(ed+1,ed+1+m,cop);
for(int i=1;i<=n;i++) p[i]=i;
int cnt=0,res=0;
for(int i=1;i<=m;i++)
{
int a=ed[i].u,b=ed[i].v,w=ed[i].w;
int x=find(a),y=find(b);
if(x!=y)
{
p[x]=y;
cnt++;
res+=w;
ans[cnt]={a,b};
}
if(cnt==n-1) break;
}
fw(res),nl;
for(int i=1;i<=n-1;i++) fw(ans[i].a),pt,fw(ans[i].b),nl;
}
void build()
{
int mina=1,minb=1;
sort(q+1,q+1+n,copa);
for(int i=2;i<=n;i++)
{
ed[++m]={q[mina].id,q[i].id,q[i].a+max(q[mina].b,q[i].b)};
if(q[i].b<q[mina].b) mina=i;
}
sort(q+1,q+1+n,copb);
for(int i=2;i<=n;i++)
{
ed[++m]={q[minb].id,q[i].id,max(q[minb].a,q[i].a)+q[i].b};
if(q[i].a<q[minb].a) minb=i;
}
}
signed main()
{
n=fr();
for(int i=1;i<=n;i++) q[i].a=fr();
for(int i=1;i<=n;i++) q[i].b=fr();
for(int i=1;i<=n;i++) q[i].id=i;
build();
kru();
return 0;
}
T3 P8958 CGOI-3 残暴圣所
数学
\(2n \to Catlan\)
把区间视为括号
考虑 \(val_{(l\,,\,r)}\)
因为 \(l\;r\) 必须把 \(1 \to 2n\) 占满
所以中间和外面必须填满括号!!!
中间任意天括号的方案 \(H(\frac{r-l-1}{2})\) 和 \(H(\frac{2n-(r-l+1)}{2})\)
\(H(n)\) 为 \(Catlan\)
综上 \(val_{(l\,,\,r)} = a_l \times a_r \times H(\frac{r-l-1}{2}) \times H(\frac{2n-(r-l+1)}{2})\)
直接枚举 \(l\;r\) 即可
如果没有条件2,就不是 \(Catlon\) 现在就是默认从左到右分配 \(idx\) 不然一个固定的括号序列 还需要考虑括号之间的编号
如果没有条件3,那么需要考虑 \(( ( ) )\) 是 1 4 2 3 两对 还是 1 3 2 4 两对
特殊性质单独处理下就行啦 枚举括号内长度为 len 的所有括号对即可
这样就拿到了前55分
\(code\)
const int N=1e6+10,Q=998244353;
int n,ans;
int a[N],H[N];
int qkw(int a,int k)
{
int ans=1,base=a;
while(k)
{
if(k&1) ans=ans*base%Q;
base=base*base%Q;
k>>=1;
}
return ans;
}
signed main()
{
n=fr();H[0]=1;
bool flag=1;
for(int i=1;i<=2*n;i++)
{
a[i]=fr();
if(a[i]!=1) flag=0;
}
for(int i=1;i<N;i++) H[i]=H[i-1]*(4*i-2)%Q*qkw(i+1,Q-2)%Q;
if(flag)
for(int len=0;len+2<=2*n;len+=2) ans=(ans+H[len/2]*H[(2*n-(len+2))/2]%Q*(2*n-(len+2)+1)%Q)%Q;
else
{
for(int l=1;l<=2*n;l++)
for(int r=l+1;r<=2*n;r+=2)
ans=(ans+(a[l]*a[r])%Q*H[(r-l-1)/2]%Q*H[(2*n-(r-l+1))/2]%Q)%Q;
}
fw(ans%Q);
return 0;
}
T4 P8971 GROI-R1 虹色的彼岸花
1
不添加没有边权的边
这样就成了一片森林,且任意两棵树之间,都没有关系
那么答案就是所有树相乘的结果
2
只要一棵树中任意一个点的点权确定了,那么剩下点的点权也可以确定!!
假设 \(val_{root}=x\)
那么每一种 \(x\) 的合法取值都对应一种该树的方案!!
所以方案数等价于 \(x\) 的范围 \(L \to R\)
\(ans*=R-L+1\)
如何计算 \(L\;R\) ?
保证每一个节点的取值在 \(l\;r\) 内
\(x \to w_1-x \to w2-w1+x \to ....\)
每个点的取值都是 \(L_i \to R_i\) 的形式
比如说 \(l \leq w_1-x \leq r\)
取交集即可
\(l \leq x+val \leq r\)
\(l \leq -x+val \leq r\)
两种情况求 \(l_i\;r_i\)
最后判断下无解的情况就行了
孤立点贡献是 \(r-l+1\) !!!!
dfs判断在递归外 是到了自己才判断 放在循环内 叶子结点没有判断!!!!
const int N=2e5+10,Q=1e9+7;
int t,n,l,r,op,u,v,w,L,R;
bool p[N];
vector<pi> as[N];
void dfs(int x,int rt,int cnt,int sum)
{
p[x]=1;
if(!(cnt&1)) L=max(L,l-sum),R=min(R,r-sum); //l-val <= x <= r-val
else L=max(L,sum-r),R=min(R,sum-l); //val-r <= x <= val-l
go(it)
{
if(it.id==rt) continue;
dfs(it.id,x,cnt^1,it.val-sum);
}
}
signed main()
{
t=fr();
while(t--)
{
n=fr(),l=fr(),r=fr();
for(int i=1;i<=n;i++) as[i].clear(),p[i]=0;
for(int i=1;i<n;i++)
{
op=fr(),u=fr(),v=fr();
if(op)
{
w=fr();
as[u].pb({v,w});
as[v].pb({u,w});
}
}
int ans=1;
for(int i=1;i<=n;i++)
{
if(!p[i])
{
L=l,R=r;
dfs(i,-1,0,0);
if(R<L) {ans=0;break;}
ans=ans*(R-L+1)%Q;
}
}
fw(ans),nl;
}
return 0;
}
T5 P8972 GROI-R1 一切都已过去
树上两点路径 \(\to\) \(Lca\)
思路很简单,维护每个节点到 \(rt=1\) 边的一个前缀乘即可
主要是这个分数比较恶心
我们知道任意分数可以写成 \(x=\frac{n}{10^m}\) 的形式
最简单的思路就是 \(pair\) 直接维护这个分数
每次约分下 有点像之前 \(CSP\) 的排污水的那个题
获得15pts高分
md3个小时+一页提交就整这破玩意
开下__int128 还是爆了
浮点数转分数:
long double w,eps=1e-5;
while(~scanf("%LF",&w))
{
int num1,num2;
if(fabsl(w-0.00)<eps) num1=0,num2=1; //==0 特判 0/1
else
{
int t=10000.0*(w+eps); //eg:0.72*10000 -> 7200 1.0001*10000 -> 100001
if(w>0.9999001) num1=t,num2=10000;//>=1
else //<1
{
int cnt=0;
while(!(t%10)) t/=10,cnt++; //cnt=2 num1=72 num2=pow(10,4-2)==100
num1=t,num2=pow(10,4-cnt); //turn(4-cnt)=pow(10,4-cnt);
}
int k=__gcd(num1,num2);
num1/=k,num2/=k;
}
fw(num1),pt,fw(num2);
}
const int N=2e5+10;
int n,q,u,v;
long double w,eps=1e-5;
ll fa[N][20],d[N];
struct qwq{
int v,nums,numf; //存边 nums 分子 numsf 分母
};
pi val[N],dot[N];
//first 分子 second 分母 val 从1到自己(包含自己)的所有边权乘积
vector<qwq> as[N];
int turn(int cnt){
if(cnt==1) return 10;
else if(cnt==2) return 100;
else if(cnt==3) return 1000;
else return 10000;
}
int gcd(int x,int y){
if(!y) return x;
else return gcd(y,x%y);
}
pi clac(int a,int b,int c,int d) // a/b * c/d 返回 a*c/b*d
{
if(!a || !c) return {0,1};
int k=gcd(a*c,b*d);
if(k) return {a*c/k,b*d/k};
else return {a*c,b*d};
}
void dfs(int x,int rt) //edge.分子 edge.分母
{
d[x]=d[rt]+1;
fa[x][0]=rt;
val[x]=clac(val[x].fi,val[x].se,val[rt].fi,val[rt].se); //乘上父亲的求前缀乘
for(int k=1;(1<<k)<=d[x];k++)
fa[x][k]=fa[fa[x][k-1]][k-1];
for(auto it:as[x])
{
if(it.v==rt) continue;
val[it.v]={it.nums,it.numf}; //儿子初始化 到儿子边的边
dfs(it.v,x); //edge
}
}
ll lca(ll x,ll y){
if(d[x]<d[y]) swap(x,y);
ll dh=d[x]-d[y],li=log2(d[x]-d[y]);
for(ll k=li;k>=0;k--) if(dh & (1<<k)) x=fa[x][k];
if(x==y) return x;
li=log2(d[x]);
for(ll k=li;k>=0;k--){
if(fa[x][k]!=fa[y][k]){
x=fa[x][k];
y=fa[y][k];
}
}
return fa[x][0];
}
void query(ll x,ll y)
{
ll z=lca(x,y);
pi ans=clac(val[x].fi,val[x].se,val[y].fi,val[y].se); //ans=x->1 * y->1
ans=clac(ans.fi,ans.se,val[z].se,val[z].fi); //ans/=lca->1
ans=clac(ans.fi,ans.se,val[z].se,val[z].fi); //除两次
ans=clac(ans.fi,ans.se,dot[x].fi,dot[x].se); //加上x的点权
// fw(ans.fi),pt,fw(ans.se),nl;
if(ans.se==1 || ans.fi==ans.se) puts("Yes");
else puts("No");
}
signed main()
{
n=fr(),q=fr();
for(int i=1;i<=n;i++) dot[i]={fr(),1}; //点权 val/1
for(int i=1;i<n;i++)
{
u=fr(),v=fr();
scanf("%Lf",&w);
int num1,num2;
if(fabsl(w-0.00)<eps) num1=0,num2=1; //==0 特判 0/1
else
{
int t=10000.0*(w+eps); //eg:0.72*10000 -> 7200 1.0001*10000 -> 100001
if(w>0.9999001) num1=t,num2=10000;//>=1
else //<1
{
int cnt=0;
while(!(t%10)) t/=10,cnt++; //cnt=2 num1=72 num2=pow(10,4-2)==100
num1=t,num2=turn(4-cnt); //turn(4-cnt)=pow(10,4-cnt);
}
int k=__gcd(num1,num2);
num1/=k,num2/=k;
}
as[u].pb({v,num1,num2});
as[v].pb({u,num1,num2});
}
val[0]=val[1]={1,1}; //边界 0->1 的边无贡献
dfs(1,0);
for(int i=1;i<=q;i++)
{
ll u,v;
u=fr(),v=fr();
query(u,v);
}
return 0;
}
正解:
只需要知道最终的答案是不是整数就行了!!!
简单来说:要消灭所有分母!!
但是10还是太大,考虑分解质因数继续优化
\(10=2 \times 5\)
维护下边前缀乘中 分解质因数了2的个数和5的个数即可
\(sum(son_2) \geq sum(father_2)\;\;and\;\;sum(son_5) \geq sum(father_5) \to Yes\)
md正解短多了
注意特判点权和边权为 \(0\) 的情况!!! 直接把 \(num2\;num5\) 设为 \(inf\) 即可
const int N=2e5+10;
int n,q,u,v,x,y,inf=1e12;
long double w,eps=1e-5;
int fa[N][20],d[N];
struct qwq{int v,num2,num5;};
pi val[N],dot[N];
vector<qwq> as[N];
int gcd(int x,int y){
if(!y) return x;
else return gcd(y,x%y);
}
void dfs(int x,int rt) //edge.分子 edge.分母
{
d[x]=d[rt]+1;
fa[x][0]=rt;
for(int k=1;(1<<k)<=d[x];k++)
fa[x][k]=fa[fa[x][k-1]][k-1];
for(auto it:as[x])
{
if(it.v==rt) continue;
val[it.v]={val[x].fi+it.num2,val[x].se+it.num5};
dfs(it.v,x); //edge
}
}
int lca(int x,int y){
if(d[x]<d[y]) swap(x,y);
int dh=d[x]-d[y],li=log2(d[x]-d[y]);
for(int k=li;k>=0;k--) if(dh & (1<<k)) x=fa[x][k];
if(x==y) return x;
li=log2(d[x]);
for(int k=li;k>=0;k--){
if(fa[x][k]!=fa[y][k]){
x=fa[x][k];
y=fa[y][k];
}
}
return fa[x][0];
}
signed main()
{
n=fr(),q=fr();
for(int i=1;i<=n;i++)
{
x=fr();
if(!x) {dot[i].fi=dot[i].se=inf;continue;}
while(!(x&1)) dot[i].fi++,x>>=1;
while(!(x%5)) dot[i].se++,x/=5;
}
for(int i=1;i<n;i++)
{
u=fr(),v=fr();
scanf("%Lf",&w);
int num1=-4,num2=-4; //先把分母的减去
if(fabsl(w-0.00)<eps) num1=inf,num2=inf; //==0 特判 0/1
else
{
int t=10000.0*(w+eps); //eg:0.72*10000 -> 7200 1.0001*10000 -> 100001
while(!(t&1)) num1++,t>>=1;
while(!(t%5)) num2++,t/=5;
}
as[u].pb({v,num1,num2});
as[v].pb({u,num1,num2});
}
dfs(1,0);
for(int i=1;i<=q;i++)
{
x=fr(),y=fr();
int z=lca(x,y);
pi ans={val[x].fi+val[y].fi-2*val[z].fi+dot[x].fi,val[x].se+val[y].se-2*val[z].se+dot[x].se};
puts(ans.fi>=0 && ans.se>=0?"Yes":"No");
}
return 0;
}
T6 P8954 VUSC Math Game
暴力+数学优化
\(N\) 的范围过大,如果直接建边显然是不行的。
根据数据范围,需要做到每次查询 \(\log\) \(n\) 级别,并且常数不能过大。
操作
操作 \(1\) :
既然不能直接建边,如何找到儿子:从自身找儿子不行,考虑从儿子找儿子。
找到每个数最小的 \(p\) ,定义为 \(p^k\) = \(q\) 且 \(k\) 最大, \(k≥2\) \(k∈N\) 。
比如 \(p(16)\) = \(2\),因为 \(2^4=16\) 。
从 \(p(x)\) 一直乘 \(p(x)\),统计 \(S(p(x))\) 集合中未被删除的数 。
模拟一个 \(16\) 。
$16 \to 2 $ 。
\(2 \to 4 \to 8 \to 16 \to 32 \to 64 \to .........\) 。
操作 \(2\) :
分析上述操作 \(1\),发现删除一个数的影响仅限于乘 \(p(x)\) 的时候统计个数会变少。
直接用 \(unorderedset\) 标记被删除的数,统计个数时判断即可。
经过一通分析,问题只剩如何找 \(p(x)\)。
考虑预处理:\(i\) 从2开始自乘,看它能更新哪些数。
用 \(unorderedmap\) 存下来所有数的 \(p(x)\) 。
如果预先存下的 \(p(x)\) 被删了,直接暴力找。
几个注意的点:
暴力找的时候精度误差会很大,对于二次根的情况可以特判。
判断根是否合法的时候,可以进行一定的增减,减小误差。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,q,op,x;
unordered_set<int> del;
unordered_map<int,int> minx; //p(x)
signed main()
{
cin>>n>>q;
for(int i=2;i<=32000;i++) //get sqrt4~sqrtmax
{
int now=i;
while(now<=n)
{
if(!minx.count(now)) minx[now]=i;
if(n/now<=i) break;
now*=i;
}
}
for(int i=1;i<=q;i++)
{
op=fr(),x=fr();
if(op==2) del.insert(x);
else
{
int k=x,cnt=0;
if(minx.count(x) && del.find(minx[x])==del.end()) k=minx[x]; //预先存的没被删
else if(abs((long long)sqrtl(x)*(long long)sqrtl(x)-x)<1e-8) k=sqrtl(x); //特殊判断下 可能二次根误差比较大
else //暴力找
{
for(int j=3;j<=60;j++)
{
if(pow(2,j)>x) break; //2^j都超过 肯定不行
int t=pow(x+0.59684,1.0/j); //增加0.5减小误差
if(abs(pow(t,j)-x)<1e-8 && del.find(t)==del.end()) k=min(k,t);
}
}
for(int j=k;j<=n;j*=k)
{
if(del.find(j)!=del.end())
{
if(n/j<k) break; //防越界
continue;
}
cnt++;
if(n/j<k) break;
}
fw(cnt);
puts("");
}
}
return 0;
}
T7 P8976 DTOI-4 排列
\(maxs=\frac{(\frac{n}{2}\,+1\,+\,n) \times \frac{n}{2}}{2}\)
无解情况: \(a>maxs\;||\;b>maxs\;||\;a+b>\frac{(n+1) \times n}{2}\)
先假定 \(a\;1\;2\;3\;4\) 这样顺着摆
\(gap = a\,-\, \frac{(1+\frac{n}{2}) \times \frac{n}{2}}{2}\)
如果 \(gap>0\) 说明还差
就把 \(1 \to \frac{n}{2}\) 每个数加上 \(\lfloor \frac{gap}{\frac{n}{2}} \rfloor\)
然后多的 从 \(\frac{n}{2}\) 逆序加 1 正序的话可能前面和后面重了
\(code\)
const int N=2e5+10;
int t,n,a,b;
int p[N];
void solve()
{
n=fr(),a=fr(),b=fr();
int maxs=(n/2+1+n)*n/4;
if(a>maxs || b>maxs || a+b>(1+n)*n/2) {puts("-1");return;}
if(!a && !b)
{
for(int i=1;i<=n;i++) fw(i),pt;
nl;return;
}
for(int i=1;i<=(n>>1);i++) p[i]=i;
int d=a-(1+n/2)*n/4;
if(d<=0) //a直接满足
{
for(int i=1;i<=n;i++) fw(i),pt;
nl;
}
else //少的加回来
{
int k=d/(n/2),idx=0;
for(int i=1;i<=(n>>1);i++) p[i]+=k;
d%=(n/2);
for(int i=n/2;i>=n/2-d+1;i--) p[i]++;
unordered_set<int> s;
for(int i=1;i<=(n>>1);i++) s.insert(p[i]);
if(s.size()!=(n>>1)) {puts("-1");return;}
for(int i=1;i<=n;i++) if(!s.count(i)) p[(n/2)+(++idx)]=i;
int res1=0,res2=0;
for(int i=1;i<=(n>>1);i++) res1+=p[i];
for(int i=(n>>1)+1;i<=n;i++) res2+=p[i];
if(res1<a || res2<b) {puts("-1");return;}
for(int i=1;i<=n;i++) fw(p[i]),pt;
nl;
}
}
signed main()
{
t=fr();
while(t--) solve();
return 0;
}
T8 P8977 DTOI-4 行走
看到这个 \(2^{i-1}\) 的东西,就像是二进制
首先 如果点权是 \(-1\) 一定不走,哪怕它的子树全是 \(1\) 都加不回来
如果有 \(1\) 一定走 \(0\) 需要特殊判断
然后字典序最小直接对 \(vector\) 排序就行了
先贪心把1排在前面,然后内部按字典序
用 \(q\) 数组记录当前走过的最优方案,\(q[i]\) 代表第 \(i\) 层选的是 1/0
如果当前层之前的最优方案 \(q[dep]=0\;and\;w[it]=1\) 直接更新,注意更新的时候,要清空原来的 \(q\)
比如原来是 \(1011\) 选了,然后清空 \(\to 1100\) 继续递归
否则还是递归 看当前子树剩下位选的 1 能不能更新最优方案
如果该层没有1,且之前的最优方案 \(q[dep]=0\) 继续递归看最优方案
记录路径就记录最后走到哪里了,然后向 \(fa[x]\) 递归判断
特判全都不选的情况!!
const int N=5e5+10;
int n,u,v,len,inf,ans;
int w[N],q[N],fa[N]; //q f[x]的类二进制表示
vector<int> as[N];
bool cop(int a,int b) {return w[a]!=w[b]?w[a]>w[b]:a<b;}
void dfs(int x,int rt,int dep)
{
fa[x]=rt;
bool one=0;
go(it)
{
if(it==rt) continue;
one|=w[it];
if(w[it]==1)
{
if(!q[dep+1]) //0 101 -> 1 000
{
q[dep+1]=1; //maxn+=(1<<dep)
ans=it;
for(int i=dep+2;i<=len;i++) q[i]=0;
len=dep+1;
//之前可能是 0 10110 现在第一个0改成1 要清空
}
dfs(it,x,dep+1); //继续递归 看当前子树是否能产生更大贡献
//因为是根据最终结尾的节点来判断的,如果当前子树能产生更大贡献
}
else if(!one && !q[dep+1]) dfs(it,x,dep+1); //没有0 尝试递归
}
}
void getpath(int x)
{
if(!(~x) || !x) return; //全部不选最优
getpath(fa[x]);
fw(x),pt;
}
signed main()
{
n=fr();
for(int i=1;i<=n;i++) w[i]=fr();
for(int i=1;i<n;i++)
{
u=fr(),v=fr();
if(w[u]==-1 || w[v]==-1) continue;
as[u].pb(v);
as[v].pb(u);
}
for(int i=1;i<=n;i++) sort(as[i].begin(),as[i].end(),cop);
//贪心把所有1放在0前面,同时按照字典序
if(w[1]==-1) return 0;
if(w[1]==1) q[1]=len=ans=1;
dfs(1,-1,1);
getpath(ans);
return 0;
}
T9 P8980 DROI Round 1 游戏
一眼数学题
\(n\) 巨大,显然是要靠数学优化
一眼样例,和质数有关,质数的个数是很少的,这样就把 \(n\) 降下来了
显然,只要一直选质数,就可以耗完小朋友,即 \(\varphi(n) \geq q\)
大致计算了下,\(\varphi(1e7)=4e6\) 够用了
考虑 \(\varphi(n) \lt q\) 的情况
找到 \(p^k \leq n\) 其中 \(k\) 为最大
出现 \(p^k\) 或其倍数则筛掉 \(p\) 这个因子,当 \([1,n]\) 内没有 任何质数的 \(k\) 次方时游戏结束
注意质数要晒到 3.3e7
const int N=3.3e7+10,Q=2e6+10;
ll n,q[Q];
int t,m,cnt;
int pr[Q<<1],phi[N];
int v[N]; //最小质因子
bool p[N],pk[N],used[N]; //是某个质数的 k 次方
void init(int x)
{
v[1]=pk[1]=1;
for(int i=2;i<=x;i++)
{
if(!p[i])
{
pr[++cnt]=i;
v[i]=i;
pk[i]=1;
}
for(int j=1;pr[j]<=x/i && j<=cnt;j++)
{
if(v[i]<pr[j]) break; //非最小质因子
int t=pr[j]*i;
v[t]=pr[j];p[t]=1;
pk[t]=(pk[i] && (v[i]==pr[j]));
}
phi[i]=phi[i-1]+(v[i]==i);
}
}
void solve()
{
n=fr(),m=fr();
for(int i=1;i<=m;i++) q[i]=fr();
if(pr[m+1]<=n)
{
puts("game won't stop");
return;
}
int res=0;
for(int i=1;i<=m;i++) used[pr[i]]=0;
for(int i=1;i<=m;i++)
{
while(q[i]*q[i]>n && !pk[q[i]]) q[i]/=v[q[i]];
//1 q[i]*q[i]<=n 求k
//2 5 x 2^2 -> 5 除成 p^k
if(q[i]*v[q[i]]>n)
{
res+=(used[v[q[i]]]==0);
used[v[q[i]]]=1;
}
//质数用完了
if(res==phi[n]) {fw(i),nl;return;}
else if(m-i+res<phi[n])
{
puts("game won't stop");
return;
}
}
}
signed main()
{
init(N-1);
t=fr();
while(t--) solve();
return 0;
}
T10 P8981「DROI」Round 1 距离
一眼dp
暴力代码 显然叶子节点才可能成为点对中的点,枚举点对,树上差分
const int N=5e6+10,Q=998244353;
int n,k,u,v,w,maxd;
int a[N],s[N],d[N],fa[N][27];
vector<int> as[N];
vector<int> leaf;
void dfs(int x,int rt)
{
d[x]=d[rt]+1;
maxd=max(maxd,d[x]);
fa[x][0]=rt;
for(int k=1;(1<<k)<=d[x];k++)
fa[x][k]=fa[fa[x][k-1]][k-1];
for(auto it : as[x])
if(it!=rt) dfs(it,x);
if(as[x].size()==1) leaf.pb(x);
}
int lca(int x,int y)
{
if(d[x]<d[y]) swap(x,y);
int dh=d[x]-d[y];
int li=log2(d[x]-d[y]);
for(int k=li;k>=0;k--) if(dh & (1<<k)) x=fa[x][k];
if(x==y) return x;
li=log2(d[x]);
for(int k=li;k>=0;k--){
if(fa[x][k]!=fa[y][k]){
x=fa[x][k];
y=fa[y][k];
}
}
return fa[x][0];
}
int dis(int x,int y)
{
int z=lca(x,y);
return d[x]+d[y]-(d[z]<<1);
}
void update(int x,int y) //差分
{
a[x]++,a[y]++;
int z=lca(x,y);
a[z]--,a[fa[z][0]]--;
}
int calc(int x,int rt)
{
int t=a[x]%Q;
go(it) if(it!=rt) t=(t+calc(it,x)%Q)%Q;
s[x]=(s[x]+t)%Q;
return t%Q;
}
int get1(int x,int rt)
{
int t=s[x]%Q;
go(it) if(it!=rt) t=(t+get1(it,x))%Q;
return t%Q;
}
int get2(int x,int rt)
{
int t=s[x]%Q*s[x]%Q;
go(it) if(it!=rt) t=(t+get2(it,x))%Q;
return t%Q;
}
signed main()
{
n=fr(),k=fr();
for(int i=1;i<n;i++)
{
u=fr(),v=fr();
as[u].pb(v);
as[v].pb(u);
}
if(n==1) {puts("1");return 0;}
if(n==2) {puts("2");return 0;}
//极远点对只可能在叶子结点产生
//求叶子结点树上差分
dfs(1,-1);
for(int i=0;i<=leaf.size()-1;i++) //枚举点对
{
for(int j=i+1;j<=leaf.size()-1;j++)
{
int x=leaf[i],y=leaf[j],flag=1,t=dis(x,y);
// if(lca(x,y)!=1) continue;
for(int k=0;k<=leaf.size()-1;k++)
{
int z=leaf[k];
if(z==x || z==y) continue;
if(dis(x,z)>t || dis(y,z)>t) {flag=0;break;}
}
if(flag) update(x,y); //极远点对
}
}
calc(1,-1);
if(k==1) fw(get1(1,-1)%Q);
else fw(get2(1,-1)%Q);
return 0;
}
正解 link
T11 P8982 DROI Round 1 下坠
1
\(f(y)=2^{a1} \times 3^{a2} \times 5^{a3} \times 7^{a4}\)
当且仅当 \(x\) 的质因子只有 2 3 5 7 时,\(x\) 为下坠数
此时 \(y= 1^{a1} \times 2^{a2} \times 4^{a3} \times 6^{a4}\)
任意 \(1 \to 10\) 的数质因子只有 2 3 5 7
2
\(y \in [1,10^{18}] \;\; f(y)_{max}=10^{18}\)
3
每个数递增因子,然后对因子组合成 \(y\)
组成 \(y\) 时候先贪心让位数最小,即比如 \(2 5\) 就变成 9 ,而不是 14。
\(code\)
const int N=1e6+10;
int n,m,q,k;
int idx[5],b[5],cost[15][5];
const int p[]={0,2,3,5,7};
struct node{
int val,res; //x y
int a[5]; //x 2 3 5 7 的指数
}f[N];
void find(int now)
{
memcpy(b,f[now].a,sizeof b);
vector<int> d;
for(int i=10;i>=2;i--)
{
bool flag=1;
while(flag) //注意是 while 能分解就一直分解
{
for(int j=1;j<=4;j++)
if(b[j]<cost[i][j]) {flag=0;break;}
if(!flag) break;
d.pb(i-1);
for(int j=1;j<=4;j++) b[j]-=cost[i][j];
}
}
reverse(d.begin(),d.end()); //贪心把小的放在前面
if(d.size()>18) f[now].res=-1;
else for(auto it:d) f[now].res=f[now].res*10+it;
}
void init()
{
for(int i=2;i<=10;i++) //对2~10质因数分解
{
int t=i;
for(int j=1;j<=4;j++)
{
while(!(t%p[j]))
{
t/=p[j];
cost[i][j]++;
}
}
}
//初始化第一个下坠数和 2 3 5 7 的指针
f[++n].val=idx[1]=idx[2]=idx[3]=idx[4]=1;
while(f[n].val<=1e18) //线性筛出1e18以内的所有下坠数
{
f[++n].val=2e18; //初始化,便于判断下面idx是否递增
for(int i=1;i<=4;i++) //转移
{
if(f[idx[i]].val*p[i]<=f[n].val) //递增最小的
{
f[n].val=f[idx[i]].val*p[i];
memcpy(f[n].a,f[idx[i]].a,sizeof f[n].a);
f[n].a[i]++;
}
}
find(n);
for(int i=1;i<=4;i++)
while(f[idx[i]].val*p[i]<=f[n].val) idx[i]++;
}
}
signed main()
{
init();
q=fr();
while(q--)
{
k=fr();
if(k>66061) fw(-1),pt;
else fw(f[k+1].res),pt;
}
return 0;
}
T12 P9008 入门赛
容斥一下,把不握手的减去
const int N=1e6+10;
int n,p,q,u,v;
unordered_set<int> f1[N],f2[N],s[N];
signed main()
{
n=fr(),p=fr(),q=fr();
int ans=n*(n-1)/2-q;
for(int i=1;i<=p;i++)
{
u=fr(),v=fr();
f1[u].insert(v),f1[v].insert(u);
}
for(int i=1;i<=q;i++)
{
u=fr(),v=fr();
f2[u].insert(v),f2[v].insert(u);
}
for(int i=1;i<=n;i++)
{
for(auto w:f1[i]) //w friend of u
{
for(auto j:f2[w])
{
if(j==i || f1[i].count(j) || f2[i].count(j)) continue;
if(!s[i].count(j) && !s[j].count(i))
{
s[i].insert(j),s[j].insert(i);
ans--;
}
}
}
for(auto w:f2[i]) //w enemy of u
{
for(auto j:f1[i])
{
if(j==i || f1[i].count(j) || f2[i].count(j)) continue;
if(!s[i].count(j) && !s[j].count(i))
{
s[i].insert(j),s[j].insert(i);
ans--;
}
}
}
}
cout<<ans;
return 0;
}
T13 P9035 KDOI-04 Pont des souvenirs
组合数学题。
首先,这种题目都要转成单增的,才可以用组合计数。
\(b_i=a_i+i-1\) 。
\(1 \leq b_1 \lt b_2 \lt b_3 \lt .... \lt b_n \leq k+n-1\) 。
显而易见 \(b_n=a_n+n-1 \geq n\) 。
每一种 \(b_n\) 的取值集合,都对应一类 \(a\) 序列方案
根据条件 \(2\) ,都满足就只需最大的满足即 \(a_{n-1}+a_n \leq k+1\) 。
\(a_{n-1} \leq \lfloor \frac{k+1}{2} \rfloor\) 。
考虑枚举最高位 \(a_n\),\(a_n\)绝对是求不了的只能枚举,\(a_n\) 的影响只在 \(a_{n-1}\)。
\(a_n=1\;a_{n-1}=1\;\;a_n=2\;a_{n-1}=1\,or\,2\;\;a_n=k\;a_{n-1}=1\)
\(a_n=\lceil \frac{k+1}{2} \rceil\;\;a_{n-1}=\lfloor \frac{k+1}{2} \rfloor\)
整个 \(a_{n-1}\) 取值类似 \(1\;2\;3\;4\;3\;2\;1\) 或者 \(1\;2\;3\;4\;4\;3\;2\;1\)
这里只算一半的方案即下取整的部分,或者说峰值左侧,因为 \(a_n\) 的取值对 \(a_{n-1}\) 的取值影响范围是确定的
所以 \(a_{n-1} \in [1,\lfloor \frac{k+1}{2} \rfloor]\),\(a_{n_{max}}= \lceil \frac{k+1}{2} \rceil\)
\(b_{n-1} \in [1,\lfloor \frac{k+1}{2} \rfloor]+n-2\)
$ans=\Sigma;C_{p+n-2}^{,n-1};;p \in [1, \lfloor \frac{k+1}{2} \rfloor] $
前面的所有数值域是 \(p+n-2\) 从值域中选 \(n-1\) 个数出来。
然后按从小到大填到序列 \(b\) 里面
根据以下公式,\(C_a^b =C_{a-1}^b + C_{a-1}^{b-1}\) 。
化简得 \(ans=C_{n-2+1}^{n}+C_{n-2+1}^{\,n-1}+C_{n-2+2}^{\,n-1}+C_{n-2+3}^{\,n-1}+...= C_{n-2+maxp+1}^{n}\)
由于 \(k\) 的奇偶性不知,这个 \(\lfloor \frac{k+1}{2} \rfloor\) 需要分类讨论一下
-
k为基:单峰值,\(a_n=a_{n-1}\) 先算 \(maxp\),再把 \(maxp\) -- 算剩下的部分也是 \(ans*2\)。
-
k为偶:双峰值,直接 \(ans*2\) 即可
至于基偶峰值,需要打表看
本题求组合数只能用阶层的方式,且求解逆元需要线性复杂度
\(code\)
const int N=2e7+10,Q=1e9+7;
int t,n,k;
int f[N],nf[N];
void init()
{
f[0]=nf[0]=f[1]=nf[1]=1; //注意1也要初始化
for(int i=2;i<N;i++)
{
f[i]=f[i-1]*i%Q;
nf[i]=nf[Q%i]*(Q-(Q/i))%Q;
}
for(int i=1;i<N;i++) nf[i]=nf[i-1]*nf[i]%Q; //转成阶层逆元
}
int C(int a,int b)
{
if(a<b) return 0;
return f[a]*nf[b]%Q*nf[a-b]%Q;
}
signed main()
{
init();
t=fr();
while(t--)
{
n=fr(),k=fr();
if(n==1) {fw(k),nl;continue;}
if(k&1)
{
int maxp=(k+1)/2;
int ans=C(n-2+maxp,n-1);
maxp--;
ans=(ans+2*C(n-2+maxp+1,n)%Q)%Q;
fw(ans),nl;
}
else
{
int maxp=(k+1)/2;
int ans=2*C(n-2+maxp+1,n)%Q;
fw(ans),nl;
}
}
return 0;
}
T14 P9036 KDOI-04 挑战 NPC III
问题等价于 \(k\) 个点的点覆盖所有边
直接二进制枚举肯定不行,得优化到 \(O(2^k),O(k^2)\) 等级别
首先贪心选度数大的点,先排序
然后度数 \(\gt k\) 的点必须选
证明:一条边如果不由 \(u\) 覆盖就得用 \(v\) 覆盖,显然不选 \(u\) 它连接的边必须由终点覆盖。
终点个数 \(=\) 度数 \(\gt k\) 不成立
考虑 \(set\) 动态维护出度, \(\gt k\) 全部删掉,然后 \(O(k)\) 更新所有相连的点,\(k--\)
等到没有点的度数 \(\gt k\) 之后,剩下的就可以随便选了,所以还得预处理一个组合数。
dfs 决策每个点删或者不删,然后贪心优化搜索顺序,同时方便判断边完全覆盖
const int N=2e5+10,K=22,Q=998244353;
int t,n,m,k,u,v,ans;
int f[N],nf[N],to[N],d[N],used[N]; //used 这个点选了
set<pi,greater<pi>> s; //存没删的点
unordered_set<int> as[N];
void init()
{
f[0]=nf[0]=1;
for(int i=1;i<N;i++)
{
f[i]=f[i-1]*i%Q;
nf[i]=nf[i-1]*qkw(i,Q-2)%Q;
}
}
int C(int a,int b)
{
if(a<b) return 0;
return f[a]*nf[b]%Q*nf[a-b]%Q;
}
void add(int x)
{
s.ins({d[x],x});
used[x]=0;
go(it)
{
if(used[it]) continue;
s.era({d[it],it});
d[it]++;
s.ins({d[it],it});
}
}
void del(int x)
{
s.era({d[x],x});
used[x]=1;
go(it)
{
if(used[it]) continue;
s.era({d[it],it});
d[it]--;
s.ins({d[it],it});
}
}
void dfs(int k,int rest) //还可以选的点数 还剩的点数
{
if(!s.size()) return; //n==k 的情况
if(!(s.begin()->first)) {ans=(ans+C(rest,k))%Q;return;} //边完全覆盖
if(!k) return; //边没有完全覆盖,但是没得选了
int x=s.begin()->second;
//1 起点覆盖
del(x);
dfs(k-1,rest-1);
add(x);
if(d[x]>k || k==rest) return;
//终点覆盖 度数又大于k 肯定不行
//k==rest 剩下的点全选,选x的方案在上面算了,下面是不选的方案
//2 终点覆盖
int q[K],st=0;
go(it) if(!used[it]) del(it),q[++st]=it;
dfs(k-st,rest-st-1); //去掉自己,避免重复计算
for(int i=st;i;i--) add(q[i]); //得倒着加 因为要判断used 否则顺序后面点的度数会变少
}
void solve()
{
n=fr(),m=fr(),k=fr();
memset(d,0,sizeof d);memset(used,0,sizeof used);
for(int i=1;i<=n;i++) as[i].clear(),to[i]=i;
s.clear(),ans=0;
for(int i=1;i<=m;i++)
{
u=fr(),v=fr();
if(!as[u].count(v))
{
as[u].ins(v),d[u]++;
as[v].ins(u),d[v]++;
}
}
sort(to+1,to+1+n,cop); //按度数排序
int idx=n;
while(k>=0 && d[to[idx]]>k)
{
for(auto it:as[to[idx]]) if(!used[it]) d[it]--; //更新终点
used[to[idx]]=1; //选这个点
idx--,k--; //注意--
}
if(k<0) {puts("0");return;} //k个点选完了都不行
for(int i=1;i<=n;i++) if(!used[i]) s.ins({d[i],i});
dfs(k,idx);
fw(ans),nl;
}
signed main()
{
init();
t=fr();
while(t--) solve();
return 0;
}
T15 P9007 入门赛

因为 \(\gcd(z,z-1)=1\) 所以转化为求 \((n-1)! \times (n-1)\) 的约数个数
简单的阶层分解 时间复杂度约为 \(O(TNlogN)\)
#include<bits/stdc++.h>
#define int long long
#define pt putchar(' ')
#define nl puts("")
#define pi pair<int,int>
#define pb push_back
#define go(it) for(auto &it:as[x]) //注意加了&
using namespace std;
const int N=1e6+10,Q=998244353;
int t,n,cnt;
int pr[N],p[N],ans[N];
void init(int n)
{
for(int i=2;i<=n;i++)
{
if(!p[i]) pr[++cnt]=i;
for(int j=1;pr[j]<=n/i;j++)
{
p[pr[j]*i]=1;
if(i%pr[j]==0) break;
}
}
}
void getdiv()
{
if(n==1)
{
puts("inf");
return;
}
unordered_map<int,int> as;
for(int i=1;i<=cnt;i++)
{
if(pr[i]>n-1) break;
int p=pr[i],k=n-1;
while(k)
{
as[p]+=k/p;
k/=p;
}
}
int x=n-1;
for(int i=1;i<=cnt;i++)
{
if(pr[i]>x) break;
if(!(x%pr[i]))
{
while(!(x%pr[i]))
{
as[pr[i]]++;
x/=pr[i];
}
}
}
int ans=1ll;
for(auto it:as) ans=ans*(it.second+1)%Q;
fw(ans),nl;
}
void solve()
{
n=fr();
getdiv();
}
signed main()
{
init(N-2);
t=fr();
while(t--) solve();
return 0;
}
考虑优化成 \(O(NlogN)\) 级别,即预处理
定义 \(f[i]=i! \times i\) 的约数个数
发现 \(f[i]\) 相比于 \(f[i-1]\) 就是多了两个 \(i\) 的因子,去掉 \(i-1\) 的因子
小技巧,质因数分解的时候 \(p\) 数组改为该数的最小质因子
const int N=1e6+10,Q=998244353;
int t,n,cnt;
int pr[N],p[N],f[N];
pi now[N];
int as[N];
void init(int n)
{
for(int i=2;i<=n;i++)
{
if(!p[i]) pr[++cnt]=p[i]=i;
for(int j=1;pr[j]<=n/i;j++)
{
p[pr[j]*i]=pr[j];
if(i%pr[j]==0) break;
}
}
}
void getdiv()
{
f[1]=1;
for(int i=1;i<N-1;i++)
{
int idx=0,x=i;
while(x)
{
if(x==1) break;
int v=p[x],s=0;
while(!(x%v))
{
x/=v;
s++;
}
now[++idx]={v,s};
}
//f[n]= f[n-1]/pr(n-1)*pr(n)*pr(n) = sum(div(n!*n))
//加上 n*n
for(int j=1;j<=idx;j++)
{
int v=now[j].first,s=now[j].second;
f[i]=f[i]*qkw(as[v]+1,Q-2)%Q;
as[v]+=s;
f[i]=f[i]*(as[v]+1+s)%Q;
}
f[i+1]=f[i];
//n+1 去除 n
for(int j=1;j<=idx;j++)
{
int v=now[j].first,s=now[j].second;
f[i+1]=f[i+1]*qkw(as[v]+1+s,Q-2)%Q;
f[i+1]=f[i+1]*(as[v]+1)%Q;
}
}
}
signed main()
{
init(N-2);
getdiv();
t=fr();
while(t--)
{
n=fr();
if(n==1) puts("inf");
else {fw(f[n-1]),nl;}
}
return 0;
}
T16 P5201 [USACO19JAN]Shortcut G
考虑最短路,发现每一头牛到牛棚的路径唯一,可以构成一颗最短路树
每次最短路更新的时候记录下是由哪个点转移的,即记录每个点的 \(pre\)
然后字典序特判一下,刚开始先 \(vector\) 排序,然后更新的时候如果 \(dis\) 相同,并且字典序更小,就更新 \(pre\) 注意,这里更新的时候不要入队!!
选择节点 \(x\) 连边,贡献只作用在自己和子树身上
记录每个点的 \(siz\),\(ans=max(ans,(d[x]-t) \times s[x])\)
const int N=1e4+10;
int n,m,u,v,w,t,ans;
int d[N],pre[N],p[N],s[N];
vector<pi> as[N];
vector<int> tr[N];
void dij()
{
priority_queue<pi,vector<pi>,greater<pi>> q;
q.push({0,1});
memset(d,0x3f,sizeof d);
memset(pre,0x3f,sizeof pre);
d[1]=0;
while(q.size())
{
auto t=q.top();
q.pop();
int num=t.second;
if(p[num]) continue;
p[num]=1;
for(auto it:as[num])
{
int id=it.first,val=it.second;
if(d[id]>d[num]+val)
{
d[id]=d[num]+val;
pre[id]=num;
q.push({d[id],id});
}
if(d[id]==d[num]+val && num<pre[id]) pre[id]=num;
}
}
}
void dfs(int x,int rt)
{
for(auto it:tr[x])
{
if(it==rt) continue;
dfs(it,x);
s[x]+=s[it];
}
ans=max(ans,(d[x]-t)*s[x]);
}
signed main()
{
n=fr(),m=fr(),t=fr();
for(int i=1;i<=n;i++) s[i]=fr();
for(int i=1;i<=m;i++)
{
u=fr(),v=fr(),w=fr();
as[u].pb({v,w});
as[v].pb({u,w});
}
for(int i=1;i<=n;i++) sort(as[i].begin(),as[i].end());
dij();
for(int i=2;i<=n;i++) tr[pre[i]].pb(i),tr[i].pb(pre[i]);
dfs(1,-1);
fw(ans);
return 0;
}
T17 P8865 [NOIP2022] 种花
当年考场上爆 \(0\),今日回首,不堪入目
首先这个求方案数,一眼 \(dp\) 然后划分集合,按 \(C\),\(F\) 的左上角 \((i,j)\) 划分集合
一个暴力代码,预处理每个点向能扩展多少,向下能扩展多少,用乘法原理算下就行了
然后几个注意的点:那个 \(C\),\(F\) 两个横之间至少要空一行,然后最后一行不能算!!
\(O(Tn^3)\)
const int N=1010,Q=998244353;
int n,m,C,F,ans1,ans2;
char op[N][N];
int down[N][N],rt[N][N];
void solve()
{
n=fr(),m=fr(),C=fr(),F=fr();
memset(down,0,sizeof down);
memset(rt,0,sizeof rt);
ans1=0,ans2=0;
for(int i=1;i<=n;i++) scanf("%s",op[i]+1);
for(int i=n;i;i--)
{
for(int j=m;j;j--)
{
if(op[i][j]=='1') {rt[i][j]=down[i][j]=0;continue;}
down[i-1][j]=(op[i][j]=='0'?down[i][j]+1:0);
rt[i][j-1]=(op[i][j]=='0'?rt[i][j]+1:0);
}
}
for(int i=1;i<=n-1;i++)
{
for(int j=1;j<m;j++)
{
if(!rt[i][j] || !down[i][j]) continue;
for(int k=2;k<=down[i][j];k++) if(rt[i+k][j]) ans1=(ans1+rt[i][j]*rt[i+k][j]%Q)%Q;
if(down[i][j]<2) continue;
for(int k=2;k<down[i][j];k++)
{
if(!rt[i+k][j] || !down[i+k][j]) continue;
ans2=(ans2+rt[i][j]*rt[i+k][j]%Q*down[i+k][j]%Q)%Q;
}
}
}
fw(ans1*C%Q),pt,fw(ans2*F%Q),nl;
}
signed main()
{
int t=fr(),id=fr();
while(t--) solve();
return 0;
}
考虑优化
可以把递推式中的 \(rt[i+k][j]\) 和 \(rt[i+k][j] \times down[i+k][j]\) 再求个和,然后用加法原理 \(O(1)\) 算贡献
\(O(Tn^2)\)
const int N=1010,Q=998244353;
int n,m,C,F,ans1,ans2;
char op[N][N];
int down[N][N],rt[N][N],sc[N][N],sf[N][N];
void solve()
{
n=fr(),m=fr(),C=fr(),F=fr();
memset(down,0,sizeof down);
memset(rt,0,sizeof rt);
memset(sc,0,sizeof sc);
memset(sf,0,sizeof sf);
ans1=0,ans2=0;
for(int i=1;i<=n;i++) scanf("%s",op[i]+1);
for(int i=n;i;i--)
{
for(int j=m;j;j--)
{
if(op[i][j]=='1') continue;
if(op[i-1][j]=='0') down[i-1][j]=down[i][j]+1; //注意两个地方都要判断
if(op[i][j-1]=='0') rt[i][j-1]=rt[i][j]+1; //同上
}
}
for(int i=n;i;i--)
for(int j=m;j;j--)
if(op[i][j]=='0') sc[i-1][j]=sc[i][j]+rt[i][j],sf[i-1][j]=sf[i][j]+rt[i][j]*down[i][j];
for(int i=1;i<n;i++)
{
for(int j=1;j<m;j++)
{
if(!rt[i][j] || !down[i][j] || op[i+1][j]=='1') continue;
ans1=(ans1+rt[i][j]*sc[i+1][j]%Q)%Q;
ans2=(ans2+rt[i][j]*sf[i+1][j]%Q)%Q;
}
}
fw(ans1*C%Q),pt,fw(ans2*F%Q),nl;
}
signed main()
{
int t=fr(),id=fr();
while(t--) solve();
return 0;
}
T18 P9148 除法题 3月月赛
首先按照复杂度可以 \(n^2\) 枚举
考虑枚举 \(a\;b\) 的值,因为下标显然无关,答案只和值域有关
那么 \(\lfloor \frac{a}{b} \rfloor\) 就知道了,考虑统计 \(\lfloor \frac{a}{c} \rfloor\;\lfloor \frac{a}{c} \rfloor\) 的数量即可
正难则反,干脆枚举 \(c\) 看哪些数对 \((a,b)\) 可以产生贡献
这个数对有一个区间假设 \(a\) 为 \([l_1,r_1]\),\(b\) 为 \([l_2,r_2]\)
两个合并起来就是一个矩形了,可以二维差分
那么只要存在一组点对 \((a,b)\) 这个 \(c\) 就会产生贡献,之后再枚举 \(a,b\) 即可
注意对 \(unsigned\) 取模的时候,输出要用 \(printf\),不然快写可能会判成负数
\(O(\Sigma_{i=1}^{v} (\frac{v}{i})^2) \to O(v^2\Sigma \frac{1}{i^2}) \to O(v^2)\)
\(\frac{1}{i^2}\) 大约是 \(\frac{3}{2}\)
const int N=5e3+10;
int n,mx;
int w[N],v[N];
unsigned ans,b[N][N];
int main()
{
n=fr();
for(int i=1;i<=n;i++)
w[i]=fr(),v[w[i]]=1,mx=max(mx,w[i]);
for(int i=1;i<=mx;i++)
{
if(!v[i]) continue;
for(int j=i<<1;j<=mx;j+=i)
for(int k=i<<1;k<=mx;k+=i)
b[j][k]++;
for(int j=i<<1;j<=mx;j+=i)
b[i+1][j]++,b[j][i+1]++;
b[i+1][i+1]++;
}
for(int i=1;i<=mx;i++)
{
for(int j=1;j<=mx;j++)
{
b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
if(i>j && v[i] && v[j]) ans+=(i/j)*b[i][j];
}
}
printf("%u",ans);
return 0;
}
T19 P3629 [APIO2010] 巡逻
考虑 \(k=1\) 的情况,不难发现连的这条边构成的换上的边全部都只会走一次
\(ans=2(n-1)-pathlen+1\)
最大化 \(pathlen\) 就是直径
直接两次 \(dfs\) 即可找直径
然后 \(k=2\)
如果和之前 \(k=1\) 的环不重合,那么就是求分离的直径
考虑重合部分,每条边需要走两次
记选择的 \(path\) 的路径长度为 \(L\)
那么一个 \(trick\) 把这些重合的边边权设为 \(-1\)
最后求出的直径就是 \(L+(-1)+(-1)+....\)
然后答案就是 \(2(n-1)-maxd+1-(L+(-1)+(-1)+....)+1\)
\(-(-1)=1\)
那么这样就被算了两次了
如何标记直径呢?
第二次 \(dfs\) 跑出来的直径另一段显然是叶子节点,那么一个节点只会有一个或零个父亲
跑 \(dfs\) 的时候标记下父亲,最后从第二次找到的端点向上爬即可
找最终的这个 \(L+(-1)+...\) 有负边权,需要用 \(dp\)
const int N=1e5+10;
int n,k,u,v,st,ed,now,ans,res;
int d[N],fa[N],vis[N];
vector<int> as[N];
void dfs(int x,int rt)
{
d[x]+=d[rt],fa[x]=rt;
if(d[x]>d[now]) now=x;
go(it)
{
if(it==rt) continue;
d[it]=1;
dfs(it,x);
}
}
void dp(int x,int rt)
{
go(it)
{
if(it==rt) continue;
int val=(vis[x] && vis[it])?-1:1;
dp(it,x);
res=max(res,d[x]+d[it]+val);
d[x]=max(d[x],d[it]+val);
}
}
int main()
{
n=fr(),k=fr();
for(int i=1;i<n;i++)
{
u=fr(),v=fr();
as[u].pb(v),as[v].pb(u);
}
dfs(1,0);
st=now,now=0;
memset(d,0,sizeof d);
memset(fa,0,sizeof fa);
dfs(st,0);
ed=now,ans=d[ed];
if(k==1) {fw(((n-1)<<1)-ans+1);return 0;}
for(int i=ed;i;i=fa[i]) vis[i]=1;
memset(d,0,sizeof d);
dp(1,0);
fw(((n-1)<<1)-ans+1-res+1);
return 0;
}
T20 P1016 [NOIP1999 提高组] 旅行家的预算
起点和终点视为 \(0\) 和 \(n+1\) 站
\(dfs\) 决策下一站去哪里
如果油够,可以直接贪心去下一站
不够可以加到刚好够,也可以梭哈
const int N=8;
int n;
double v,m,D,ans=2e9;
pair<double,double> val[N];
//当前第几个车站 剩余油量 当前花费
void dfs(int x,double rest,double w)
{
if(rest<0 || rest>v || w>ans) return;
if(x==n+1) {ans=w;return;}
for(int i=x+1;i<=n+1 && (val[i].d-val[x].d)/m<=v;i++)
{
if((val[i].d-val[x].d)/m<=rest) dfs(i,rest-(val[i].d-val[x].d)/m,w);
else dfs(i,0,w+((val[i].d-val[x].d)/m-rest)*val[x].p);
dfs(i,v-(val[i].d-val[x].d)/m,w+(v-rest)*val[x].p);
}
}
int main()
{
scanf("%lf%lf%lf%lf%d",&D,&v,&m,&val[0].p,&n);
val[n+1].d=D;
for(int i=1;i<=n;i++) scanf("%lf%lf",&val[i].d,&val[i].p);
sort(val+1,val+1+n);
dfs(0,0,0);
if(ans==2e9) puts("No Solution");
else printf("%.2lf",ans);
return 0;
}
T21 P8110 [Cnoi2021]矩阵

const int N=1e5+10,Q=998244353;
int n,k,s1,s2,s3;
int a[N],b[N];
signed main()
{
n=fr(),k=fr();
if(!k) {fw(n);return 0;}
for(int i=1;i<=n;i++) a[i]=fr(),s1=(s1+a[i]+Q)%Q;
for(int i=1;i<=n;i++) b[i]=fr(),s2=(s2+b[i]+Q)%Q;
for(int i=1;i<=n;i++) s3=(s3+(a[i]*b[i]%Q)+Q)%Q;
fw(s1*s2%Q*qkw(s3,k-1)%Q);
return 0;
}
T22 P6722 「MCOI-01」Village 村庄
显然有枚举点对暴力 \(lca\) 建边+二分图染色判定的 \(O(n^2logn+n^2+n)\) 的做法
但是本题只要求是否满足,我们考虑什么情况不满足
我们知道二分图不成立的充要条件是有奇数环
我们考虑一个奇数环,若新图中有 \((u,v)\) 则对 \(x\in T_u\),必有 \((x,v)\)
则有环 \((u,v)(u,x)(x,v)\)
如果一个点到直径的两个端点的距离都 \(\geq k\) 那么显然可以形成一个奇数环
当然也可以换根 \(dp\) 记录到自己最远的三个点
其中两个和自己配,或者三个单独配
T23 P7976 「Stoi2033」园游会
对于这类取模的问题,我们可以直接把负数转成正数再打表,这样好看一点
\(%p\) 可以考虑 \(p\) 进制数分解
https://www.luogu.com.cn/blog/xX613723-RICHARD/solution-p7976
const int N=310,Q=1732073999;
int n;
int base[N],a[N];
const int f[3]={1,2,1},p[3]={0,1,3};
signed main()
{
int T=fr(),_T=fr();
base[1]=1;
for(int i=2;i<N;i++) base[i]=base[i-1]*4%Q;
while(T--)
{
int n=fr();
n++;
int len=0,ans=0,lt=1;
while(n)
{
a[++len]=n%3;
n/=3;
}
for(int i=len;i;i--)
{
ans=(ans+p[a[i]]*lt*base[i])%Q;
lt=lt*f[a[i]]%Q;
}
fw(ans),nl;
}
return 0;
}
T24 P5687 [CSP-S2019 江西] 网格图
显然的 \(kru\) 建边优化题
不同的边只有 \(n+m\) 种,我们按套路排序 \(a\;b\),每次选择较小的边权加入集合
注意必须先选 \(a_1\;b_1\) 两类边保证连通性,这是所有优化 \(kru\) 必须保证的,如 \(T2\)
const int N=3e5+10;
int n,m,cnt,ans;
int a[N],b[N]; //向右,向下
signed main()
{
n=fr(),m=fr();
for(int i=1;i<=n;i++) a[i]=fr();
for(int j=1;j<=m;j++) b[j]=fr();
sort(a+1,a+1+n);
sort(b+1,b+1+m);
int idx1=2,idx2=2,rest1=n-1,rest2=m-1; //剩多少行 列
ans=a[1]*(m-1)+b[1]*(n-1);
while(idx1<=n && idx2<=m)
{
if(cnt>=n*m-1) break;
if(a[idx1]<=b[idx2]) //行
{
ans+=rest2*a[idx1];
cnt+=rest2;
rest1--,idx1++;
}
else //列
{
ans+=rest1*b[idx2];
cnt+=rest1;
rest2--,idx2++;
}
}
fw(ans);
return 0;
}
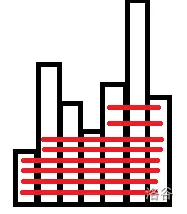
T25 P6801 [CEOI2020] 花式围栏
矩形题,一眼单调栈
我们规定当前点为矩形的右边界划分集合,宽度只是加权,高度才是影响的关键
首先如何求一个 \(n \times m\) 的矩形内部有多少个子矩形
一个矩形任选两条衡边和两条纵边,\(n+1 \choose 2\) \(\times\) \(m+1 \choose 2\)
单调栈维护上升序列,每次在高度下降的时候算答案,把高的部分全部削掉,削掉的时候算上他们的高出的小矩形答案

const int N=1e5+10,Q=1e9+7;
int n,ans,top;
int h[N],w[N],ak[N];
int calc(int x){return (x*(x+1)/2)%Q;}
signed main()
{
n=fr();
for(int i=1;i<=n;i++) h[i]=fr();
for(int i=1;i<=n;i++) w[i]=fr();
for(int i=1;i<=n+1;i++) //最后一个不一定是最矮的,要往后搞一位
{
int s=0;
while(h[ak[top]]>h[i])
{
int lt=ak[top--];
(s+=w[lt])%=Q; //高出部分宽的后缀和
(ans+=(calc(h[lt])-calc(max(h[i],h[ak[top]]))+Q)%Q*calc(s)%Q)%=Q;
}
(w[i]+=s)%=Q;
ak[++top]=i;
}
fw(ans);
return 0;
}
T26 P6767 [BalticOI 2020/2012 Day0] Roses
设 \(a\) 朵 \(b\) 元方案是性价比最高的
先贪心全买 \(A\)
考虑买多少组 \(C\)
如果 \(i \times c \equiv 0 \pmod a\),那么买 \(i\) 组 \(c\),不如买 $ \frac {i\times c}{a} $ 组 \(a\)
所以让 \(i\) 枚举到 \(\frac {a}{\gcd (a,c)}\) 即可
可以认为是一个构造结论
int n,A,B,C,D,ans;
int cost(int x)
{
if(x<=0) return 0;
return ((x+A-1)/A)*B;
}
signed main()
{
n=fr(),A=fr(),B=fr(),C=fr(),D=fr();
if(A*D<B*C) swap(A,C),swap(B,D);
ans=cost(n);
int limit=A/__gcd(A,C);
for(int i=1;i<=limit;i++)
ans=min(ans,i*D+cost(n-i*C));
fw(ans);
return 0;
}
T27 P7162 [COCI2020-2021#2] Sjekira
一个显然的贪心,权值大的点连的边必须优先删除掉,不然留着更亏
\(O(n^2)\)
const int N=2e5+10;
int n,u,v,ans,p=1000;
int w[N],id[N],vis[N];
unordered_map<int,bool> used;
vector<int> as[N];
bool cop(int a,int b){return w[a]>w[b];}
int dfs(int x,int rt)
{
int res=w[x];
go(v) if(v!=rt && used[min(x,v)*p+max(x,v)]) res=max(res,dfs(v,x));
return res;
}
signed main()
{
n=fr();
for(int i=1;i<=n;i++) w[i]=fr(),id[i]=i;
for(int i=1;i<n;i++)
{
u=fr(),v=fr();
as[u].pb(v),as[v].pb(u);
used[min(u,v)*p+max(u,v)]=1;
}
sort(id+1,id+1+n,cop);
for(int j=1;j<=n;j++)
{
int i=id[j];
for(auto &v:as[i])
if(used[min(i,v)*p+max(i,v)]) ans+=w[i]+dfs(v,i),used[min(i,v)*p+max(i,v)]=0;
}
fw(ans);
return 0;
}
经典删边转加边,并查集维护
\(O(n\log n)\)
注意每次加边只加权值更小的点 权值更大的点的连的点边只能在更大的时候连
因为正着的时候相当于是权值大的先选择,这条边是“属于”它的,只有比自己权值小的点所成的边是自己的
const int N=2e5+10;
int n,u,v,ans;
int w[N],id[N],p[N],vis[N];
vector<int> as[N];
bool cop(int a,int b){return w[a]<w[b];}
int find(int x)
{
if(x!=p[x]) p[x]=find(p[x]);
return p[x];
}
signed main()
{
n=fr();
for(int i=1;i<=n;i++) w[i]=fr(),p[i]=id[i]=i;
for(int i=1;i<n;i++)
{
u=fr(),v=fr();
as[u].pb(v),as[v].pb(u);
}
sort(id+1,id+1+n,cop);
for(int i=1;i<=n;i++)
{
int x=id[i];
vis[x]=1;
go(v)
{
int px=find(x),pv=find(v);
if(vis[v] && px!=pv) //只加权值更小的点 权值更大的点的连的点边只能在更大的时候连
{
ans+=(w[px]+w[pv]);
p[px]=pv;
w[pv]=max(w[pv],w[px]);
}
}
}
fw(ans);
return 0;
}
T28 P7149 [USACO20DEC] Rectangular Pasture S
首先每个点的 \((x,y)\) 都不同,我们可以做一下二维离散化,转成一个 \(N \times N\) 的网格
现在在矩形中枚举就是任意包含的一个牛点集,枚举的矩形必须边线上有牛,否则可以有更小的相同点集举行,只要最小矩形,这样就不会算重了
对牛按 \(y\) 排序
我们枚举矩形上下两条线,然后借助恰好 \(y\) 在两条线上的牛来算
假定 \([y_a,y_b]\) \(a\;b\) 是线上的两头牛
那么矩形还剩的左右两条线依靠,\(y\) 在这个 \([y_a,y_b]\) 区间,且 \(x\) 在 \([1,min(x_a,x_b)]\) 区间的可以作为围栏的左边界,\(x\) 在 \([max(x_a,x_b),n]\) 区间的都可以作为围栏的右边界,根据乘法原理可的答案为 \(cnt_1 \times cnt_2\) (左右两侧牛数)
const int N=2510;
int n,ans;
int x[N],y[N],s[N][N];
pi pos[N];
bool cop(pi a,pi b){return a.se<b.se;}
int calc(int x1,int y1,int x2,int y2){return s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1];}
signed main()
{
n=fr();
for(int i=1;i<=n;i++) pos[i]={x[i]=fr(),y[i]=fr()};
sort(pos+1,pos+1+n,cop);
sort(y+1,y+1+n),sort(x+1,x+1+n);
for(int i=1;i<=n;i++)
{
pos[i].fi=lower_bound(x+1,x+1+n,pos[i].fi)-x;
pos[i].se=lower_bound(y+1,y+1+n,pos[i].se)-y;
s[pos[i].fi][pos[i].se]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
s[i][j]+=s[i][j-1]+s[i-1][j]-s[i-1][j-1];
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++)
ans+=calc(1,pos[i].se,min(pos[i].fi,pos[j].fi),pos[j].se)*calc(max(pos[i].fi,pos[j].fi),pos[i].se,n,pos[j].se);
fw(ans+1);
return 0;
}
T29 P7100 [W1] 团
暴力建边 \(O(|S|^2)\),我们需要降到 \(O(|S|)\)
本质是集合内部所有点联通,常用技巧,菊花图一样建个虚点,都向虚点连边即可
\(O((N+K)\log (N+K))\)
signed main()
{
n=fr(),k=fr();
for(int i=1;i<=k;i++)
{
int cnt=fr();
for(int j=1;j<=cnt;j++)
{
int a=fr(),b=fr();
as[a].pb({n+i,b});
as[n+i].pb({a,b});
}
}
dij();
return 0;
}
T30 P6503 [COCI2010-2011#3] DIFERENCIJA
显然把式子拆开算,维护自己为区间最大/小值的区间,但是这样碰到数值相等的情况就会出现问题
问题就在两个相等的数如果区间相交就会算重,我们改成前开后闭,这样没有重复的数不影响,有重复的数无交集
同时任选包含自己的区间是左边选一个括号右边选一个括号乘起来,和 \(T28\) 比较像
const int N=3e5+10;
int n,top,ans;
int a[N],ak[N];
int maxl[N],maxr[N],minl[N],minr[N];
int calc(int x,int y,int z) {return (y-x+1)*(z-y+1);}
signed main()
{
n=fr();
for(int i=1;i<=n;i++) a[i]=fr();
for(int i=1;i<=n;i++)
{
while(top && a[ak[top]]<=a[i]) top--; //开区间
if(top) maxl[i]=ak[top]+1;
else maxl[i]=1;
ak[++top]=i;
}
top=0;
for(int i=n;i;i--)
{
while(top && a[ak[top]]<a[i]) top--; //闭区间
if(top) maxr[i]=ak[top]-1;
else maxr[i]=n;
ak[++top]=i;
}
top=0;
for(int i=1;i<=n;i++)
{
while(top && a[ak[top]]>=a[i]) top--; //开区间
if(top) minl[i]=ak[top]+1;
else minl[i]=1;
ak[++top]=i;
}
top=0;
for(int i=n;i;i--)
{
while(top && a[ak[top]]>a[i]) top--; //闭区间
if(top) minr[i]=ak[top]-1;
else minr[i]=n;
ak[++top]=i;
}
for(int i=1;i<=n;i++)
{
ans+=a[i]*(calc(maxl[i],i,maxr[i])-calc(minl[i],i,minr[i]));
// fw(a[i]),pt,fw(maxl[i]),pt,fw(maxr[i]),pt,fw(minl[i]),pt,fw(minr[i]),nl;
}
fw(ans);
return 0;
}
T31 P7299 [USACO21JAN] Dance Mooves S
我们先走一次,然后记录每个位置最终是哪头牛
暴力方法就是直接走 \(n\) 此,\(O(nk)\)
考虑优化,即每个位置 \(i\) 第一次最终是牛 \(bel_i\)
那么 \(bel_i\) 在第二个 \(K\) 训循环内会走一遍第一次 $$K$ 循环牛 \(i\) 的老路,牛 \(i\) 也会这样走,我们发现不断下去构成了一个环
考虑并查集!!!!(老是忘记它)
直接合并同一个环内的牛
const int N=2e5+10;
int n,k;
int a[N],b[N],bel[N],p[N];
unordered_set<int> vis[N],ans[N];
int find(int x)
{
if(x!=p[x]) p[x]=find(p[x]);
return p[x];
}
int main()
{
n=fr(),k=fr();
for(int i=1;i<=k;i++) a[i]=fr(),b[i]=fr();
for(int i=1;i<=n;i++) p[i]=bel[i]=i,vis[i].insert(i);
for(int i=1;i<=k;i++)
{
int x=a[i],y=b[i];
int px=bel[x],py=bel[y];
vis[px].insert(y),vis[py].insert(x);
swap(bel[x],bel[y]);
}
for(int i=1;i<=n;i++) p[find(i)]=find(bel[i]);
for(int i=1;i<=n;i++)
for(auto v:vis[bel[i]])
ans[find(bel[i])].insert(v);
for(int i=1;i<=n;i++) fw(ans[find(i)].size()),nl;
return 0;
}
T32 P7300 [USACO21JAN] No Time to Paint S
对于这种中间空着的,就维护前后缀
\(Q\) 很多预处理!!
显然,深色不影响浅色,浅色影响深色
如果之前有某个颜色 \(col\),并且没碰到比它更浅的颜色,现在就不用再染色了
值域又很小,可以搞个桶记下之前是否出现自己
然后每次把比自己深的颜色清空,因为那些深的颜色无法染色到自己
const int N=1e5+10;
int n,q,l,r;
int a[N],f[N],g[N];
bool vis[30];
string s;
void prework()
{
for(int i=1;i<=n;i++)
{
f[i]=f[i-1];
for(int j=a[i]+1;j<=26;j++) vis[j]=0;
if(!vis[a[i]]) vis[a[i]]=1,f[i]++;
}
memset(vis,0,sizeof vis);
for(int i=n;i;i--)
{
g[i]=g[i+1];
for(int j=a[i]+1;j<=26;j++) vis[j]=0;
if(!vis[a[i]]) vis[a[i]]=1,g[i]++;
}
}
int main()
{
n=fr(),q=fr();
cin>>s;
for(int i=1;i<=n;i++) a[i]=s[i-1]-'A'+1;
prework();
while(q--)
{
l=fr(),r=fr();
fw(f[l-1]+g[r+1]),nl;
}
return 0;
}
T33 P7284 [COCI2020-2021#4] Patkice II
考虑 \(spfa\) 网格最短路
传统方法就是记录每个点的状态,然后转移
但是实际上我们不需要记录每个点的状态,每次就直接四个方向转移,如果转移的方向不是原来地图洋流的方向,就边权 \(+1\) 即可
但是这样就不能用 \(vis\) 数组,因为状态不同,\(d\) 不同
边权只有 \(0/1\) 可以 \(slf\) 优化
const int N=2e3+10;
int n,m,sx,sy,ex,ey;
int a[N][N],d[N][N];
bool vis[N][N];
string s;
unordered_map<char,int> id;
struct node{int x,y,d;};
struct path{int x,y;};
path pre[N][N];
const int dx[]={0,0,0,1,-1};
const int dy[]={0,1,-1,0,0};
const char to[]={'o','>','<','v','^','.','x'};
bool ck(int x,int y){return (x>=1 && x<=n && y>=1 && y<=m);}
void print()
{
//[tx,ty,tv] -> [x,y,v]
int x=pre[ex][ey].x,y=pre[ex][ey].y;
int tx=ex,ty=ey;
//右左下上
while(x!=sx || y!=sy)
{
if(x==tx && y==ty-1) a[x][y]=1;
else if(x==tx && y==ty+1) a[x][y]=2;
else if(x==tx-1 && y==ty) a[x][y]=3;
else if(x==tx+1 && y==ty) a[x][y]=4;
tx=x,ty=y;
x=pre[tx][ty].x,y=pre[tx][ty].y;
}
fw(d[ex][ey]),nl;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++) cout<<to[a[i][j]];
nl;
}
}
void spfa()
{
memset(d,0x3f,sizeof d);
deque<node> q;
q.pb({sx,sy,0});
d[sx][sy]=0;
while(q.size())
{
auto t=q.front();
q.pop_front();
for(int i=1;i<=4;i++)
{
int xx=t.x+dx[i],yy=t.y+dy[i];
if(ck(xx,yy) && d[xx][yy]>t.d+(i!=a[t.x][t.y] && a[t.x][t.y]!=0))
{
d[xx][yy]=t.d+(i!=a[t.x][t.y] && a[t.x][t.y]!=0),pre[xx][yy]={t.x,t.y};
if(q.size() && d[xx][yy]<d[q.front().x][q.front().y]) q.push_front({xx,yy,t.d+(i!=a[t.x][t.y] && a[t.x][t.y]!=0)});
else q.pb({xx,yy,t.d+(i!=a[t.x][t.y] && a[t.x][t.y]!=0)});
}
}
}
print();
}
int main()
{
id['>']=1,id['<']=2,id['v']=3,id['^']=4,id['.']=5;
n=fr(),m=fr();
for(int i=1;i<=n;i++)
{
cin>>s;
for(int j=0;j<m;j++)
{
if(s[j]=='o') sx=i,sy=j+1;
else if(s[j]=='x') ex=i,ey=j+1,a[i][j+1]=6;
else a[i][j+1]=id[s[j]];
}
}
spfa();
return 0;
}
T34 P6812 「MCOI-02」Ancestor 先辈
问题等价于,把所有后面的数和前面对齐,后面的数都要比前面的大,等价于区间是否不下降!!
证明
反证,考虑区间 \([l,r]\),若 \(\exists i \lt j,a_i \gt a_j\)
我们取后缀 \([l,i]\) \([j-(i-l),j,r]\),使 \(i,j\) 对齐,这样就够造出了一个不合法的后缀
线段树维护,区间是否不下降,左端点右端点值
要开 \(long\,long\) !!
const int N=1e6+10;
int n,k;
int a[N];
struct node{
int l,r;
bool ok;
int vl,vr,add;
}tr[N*4];
void chf(int idx)
{
node &t=tr[idx],&ls=tr[idx<<1],&rs=tr[idx<<1|1];
t.ok=(ls.ok && rs.ok && ls.vr<=rs.vl);
t.vl=ls.vl,t.vr=rs.vr;
}
void chs(int idx)
{
node &t=tr[idx],&ls=tr[idx<<1],&rs=tr[idx<<1|1];
if(t.add)
{
ls.add+=t.add,rs.add+=t.add;
ls.vl+=t.add,ls.vr+=t.add;
rs.vl+=t.add,rs.vr+=t.add;
t.add=0;
}
}
void build(int ql,int qr,int idx)
{
tr[idx]={ql,qr};
if(ql==qr)
{
tr[idx].vl=tr[idx].vr=a[ql];
tr[idx].ok=1;
return;
}
int mid=(ql+qr)>>1;
build(ql,mid,idx<<1);
build(mid+1,qr,idx<<1|1);
chf(idx);
}
void modify(int ql,int qr,int idx,int x)
{
node &t=tr[idx];
if(ql<=t.l && qr>=t.r)
{
t.add+=x,t.vl+=x,t.vr+=x;
return;
}
chs(idx);
int mid=(t.l+t.r)>>1;
if(ql<=mid) modify(ql,qr,idx<<1,x);
if(qr>mid) modify(ql,qr,idx<<1|1,x);
chf(idx);
}
bool query(int ql,int qr,int idx)
{
node &t=tr[idx];
if(ql<=t.l && qr>=t.r)
return t.ok;
chs(idx);
int mid=(t.l+t.r)>>1;
if(qr<=mid) return query(ql,qr,idx<<1);
else if(ql>mid) return query(ql,qr,idx<<1|1);
else return (query(ql,qr,idx<<1) && query(ql,qr,idx<<1|1) && tr[idx<<1].vr<=tr[idx<<1|1].vl);
}
signed main()
{
n=fr(),k=fr();
for(int i=1;i<=n;i++) a[i]=fr();
build(1,n,1);
while(k--)
{
int op=fr(),l=fr(),r=min(n,fr());
if(op==1) modify(l,r,1,fr());
else puts(query(l,r,1)?"Yes":"No");
}
return 0;
}
T35 P7716 「EZEC-10」Covering
只能按编号顺序放,我们考虑从大到小放
分类讨论编号 \(x\) 的卡牌,比它编号大的牌都放好了
\(1\) 出现 \(2\) 次,因为保证合法,所以只有一种摆法
\(2\) 出现 \(1\) 次,只要旁边格子的编号比它大,它就可以和那个格子形成一种方案,所以看它旁边有几个空是放了牌的
\(3\) 出现 \(0\) 次,如果要选,则必须由更大号卡牌覆盖,图上所有已经放过牌的地方都可以放
对于情况 \(1\) 和 \(2\) 我们都可以通过扫描解决
而对于情况 \(3\) 我们选择的情况是任意的
每次把可选的情况数记下来
设情况 \(1,2\) 共出现了 \(t\) 种纸牌,我们还要选 \([l-t,r-t]\) 张纸牌,这些从没出现(情况3)里面任选就是 \(01\) 背包问题
const int N=1e3+10,Q=1e9+7;
int n,m,k,l,r;
int a[N][N],ans[N],sum[N];
bool vis[N][N];
vector<pi> card[N];
const int dx[]={0,0,-1,1};
const int dy[]={1,-1,0,0};
int cnt(int x,int y)
{
int res=0;
for(int i=0;i<4;i++) res+=(vis[x+dx[i]][y+dy[i]]!=0);
vis[x][y]=1;
return res;
}
void solve()
{
n=fr(),m=fr(),k=fr(),l=fr(),r=fr();
for(int i=1;i<=k;i++) card[i].clear();
memset(ans,0,sizeof ans);
memset(vis,0,sizeof vis);
memset(sum,0,sizeof sum);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
a[i][j]=fr();
if(a[i][j]) card[a[i][j]].pb({i,j});
}
int t=0,lim=1,res=0,appear=1,comb=0;
for(int i=1;i<=k;i++)
if(card[i].size()) t++,lim=i;
for(int i=lim;i;i--)
{
if(card[i].size()==2)
{
ans[i]=1;
(comb+=cnt(card[i][0].fi,card[i][0].se))%=Q;
(comb+=cnt(card[i][1].fi,card[i][1].se))%=Q;
}
else if(card[i].size()==1)
{
ans[i]=cnt(card[i][0].fi,card[i][0].se);
(comb+=ans[i])%=Q;
(appear*=ans[i])%=Q;
}
else ans[i]=comb;
}
sum[0]=1;
for(int i=1;i<=lim;i++)
if(!card[i].size())
for(int j=k-t;j;j--)
(sum[j]+=sum[j-1]*ans[i]%Q)%=Q;
for(int i=max(l,t);i<=min(lim,r);i++)
(res+=appear*sum[i-t]%Q)%=Q;
fw(res),nl;
}
signed main()
{
int T=fr();
while(T--) solve();
return 0;
}
T36 P6627 [省选联考 2020 B 卷] 幸运数字
区间这么大范围,显然不能枚举
三个操作都可以等价于区间操作
\(1\) \([L,R]\) \(\oplus\,x\)
\(2\) \([A,A]\) \(\oplus\,x\)
\(3\) \((-\infty,B-1] \cup [B+1,\infty)\) \(\oplus\,x\)
看到题目中有这句话
如果有多个幸运数字能够得到最大优惠额度,输出绝对值最小的那个。如果还有多个,则输出值最大的。
考虑最终答案的区间 \([L_1,R_1]\) \([L_2,R_2]\) ....
如果全部都在正半轴 \(0...L_1...R_1\) 类型 显然取 \(L_1\)
负半轴同理,如果正负半轴都有 \(L_1...0...R_1\) 显然取 \(0\)
答案只可能在区间端点/0出现,离散化这些点即可
考虑离散化区间的时候,要么用一个点代表一个区间,要么就考虑区间端点
只用最终查询一次,查分修改即可
const int N=4e5+10;
int n,cnt,len,ans,pos;
int op[N],L[N],R[N],w[N];
int dot[N],d[N];
signed main()
{
n=fr();
dot[++cnt]=0;
for(int i=1;i<=n;i++)
{
op[i]=fr();
if(op[i]==1)
{
dot[++cnt]=L[i]=fr(),dot[++cnt]=R[i]=fr(),w[i]=fr();
dot[++cnt]=L[i]-1,dot[++cnt]=R[i]+1;
}
else
{
L[i]=fr(),w[i]=fr();
dot[++cnt]=L[i],dot[++cnt]=L[i]-1,dot[++cnt]=L[i]+1;
}
}
sort(dot+1,dot+1+cnt);
len=unique(dot+1,dot+1+cnt)-dot-1;
for(int i=1;i<=n;i++)
{
L[i]=lower_bound(dot+1,dot+1+len,L[i])-dot;
if(op[i]==1)
{
R[i]=lower_bound(dot+1,dot+1+len,R[i])-dot;
d[L[i]]^=w[i],d[R[i]+1]^=w[i];
}
else if(op[i]==2) {d[L[i]]^=w[i],d[L[i]+1]^=w[i];}
else {d[1]^=w[i],d[L[i]]^=w[i],d[L[i]+1]^=w[i];}
}
for(int i=1;i<=len;i++)
{
d[i]^=d[i-1];
if(ans<d[i]) ans=d[i],pos=dot[i];
else if(ans==d[i] && (abs(pos)>abs(dot[i]) || (abs(pos)==abs(dot[i]) && dot[i]>pos))) pos=dot[i];
}
fw(ans),pt,fw(pos);
return 0;
}
T37 P6659 [POI 2019] Najmniejsza wspólna wielokrotność
\(M \leq 10^{18}\) 自然想到 \(\sqrt[3]{M}\)
观察到样例的答案区间长度不是 \(2\) 就是 \(3\)
长度为 \(2\) \(M=l(l+1)\)
长度为 \(3\) 考虑 \(M\) 的奇偶性
\(M\) 为奇 \(M=l(l+1)(l+2)\) \(l\) 为奇
\(M\) 为偶 \(M=\frac{l(l+1)(l+2)}{2}\) \(l\) 为偶
直接开平方根和三次方根暴力找
如果区间长度 \(\gt 3\) 又 \(19! \lt 10^{18} \lt 20!\) 区间长度在 \([4,19]\) 之间
当区间长度 \(\gt 4\) 直接用 \(map\) 暴力预处理存一下就行了,数量很少
const int P=1e9;
int n,inf=1e18;
unordered_map<int,int> mp;
int gcd(int a,int b){return (!b)?a:gcd(b,a%b);}
int lcm(int a,int b){return a/gcd(a,b)*b;}
void prework()
{
for(int l=1;l<=1500000;l++)
{
int now=l*(l+1);
for(int r=l+2;;r++)
{
if(now>inf || now<0) break;
now=lcm(now,r);
if(now>inf || now<0) break;
if(!mp.count(now)) mp[now]=l*P+r;
}
}
}
void solve(int x)
{
if(mp.count(x)) {fw(mp[x]/P),pt,fw(mp[x]%P),nl;return;}
int k=sqrtl(x)+0.38975;
if(k*(k+1)==x) {fw(k),pt,fw(k+1),nl;return;}
puts("NIE");
}
signed main()
{
prework();
n=fr();
for(int i=1;i<=n;i++) solve(fr());
return 0;
}
T38 P6600 「EZEC-2」字母
好像种花
枚举左上角的点,然后暴力枚举长度转移 \(O(n^3)\)
我们不妨枚举 \(T\) 中间那个横竖交叉的点
设每个点向左/右/下最多 \(L,R,D\)
考虑这样的一组能形成多少 \(T\) 形
设 \(G(w,h)\) 若满足
\(G(w,h)\) 为 \(1\)
\(F(w,h)\) 为 \(G(w,h)\) 的前缀和
const int N=3e3+10;
int n,m,aa,b,s,x,ans;
int a[N][N],r[N][N],l[N][N],d[N][N],f[N][N];
string ss;
signed main()
{
n=fr(),m=fr(),aa=fr(),b=fr(),s=fr(),x=fr();
for(int i=1;i<=n;i++)
{
cin>>ss;
for(int j=1;j<=m;j++) a[i][j]=ss[j-1]-'0';
}
for(int i=1;i<=n;i++)
for(int j=m;j;j--)
if(a[i][j]) r[i][j]=r[i][j+1]+1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(a[i][j]) l[i][j]=l[i][j-1]+1;
for(int i=n;i;i--)
for(int j=1;j<=m;j++)
if(a[i][j]) d[i][j]=d[i+1][j]+1;
int k=max(n,m);
for(int i=max(aa,3);i<=k;i++)
for(int j=max(b,2);j<=k;j++)
{
f[i][j]=(i*j>=s && i+j>=x && i&1);
f[i][j]+=f[i-1][j]+f[i][j-1]-f[i-1][j-1];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
ans+=f[max(0,min(l[i][j],r[i][j])*2-1)][d[i][j]];
fw(ans);
return 0;
}
T39 P4377 [USACO18OPEN] Talent Show G
看到分数形最大值,想到 \(0/1\) 分数规划
二分答案
记 \(c_i=t_i-mid \times w_i\)
问题转化为,选出一些牛,能否使方案中
const int N=260,M=1e3+10;
int n,m;
double s;
int v[N],w[N];
double c[N],f[M];
bool check(double x)
{
for(int i=1;i<=n;i++) c[i]=1.0*w[i]-x*v[i];
for(int i=1;i<=m;i++) f[i]=-2e9;
for(int i=1;i<=n;i++)
for(int j=m;~j;j--)
f[min(m,j+v[i])]=max(f[min(m,j+v[i])],f[j]+c[i]);
return f[m]>=0;
}
int main()
{
n=fr(),m=fr();
for(int i=1;i<=n;i++) v[i]=fr(),w[i]=fr(),s=max(s,1.0*w[i]/v[i]);
double l=0,r=s;
while(r-l>1e-6)
{
double mid=(l+r)/2;
if(check(mid)) l=mid;
else r=mid;
}
fw((int)(l*1000));
return 0;
}
T40 P7875 「SWTR-07」IOI 2077
序列升序,考虑枚举 \(m\),设 \([l,k-1]\) 长 \(L\),\([k+1,r]\) 长 \(R\)
则此次贡献为
考虑每个元素出现的次数,然后 \([l,k-1]\) 每个元素等价,\([k+1,r]\) 同理
特殊处理 \(m=0\) 贡献为 \(a_k\)
\(O(nq\log q)\)
\(61pts\)
const int N=2e6+10,Q=998244353;
int n,q,l,r,p,ans;
int a[N],fac[N],nf[N],s[N];
int qkw(int a,int k)
{
int ans=1,base=a;
while(k)
{
if(k&1) ans=ans*base%Q;
base=base*base%Q;
k>>=1;
}
return ans;
}
int C(int a,int b)
{
if(a<b) return 0;
return fac[a]*nf[b]%Q*nf[a-b]%Q;
}
void prework()
{
fac[0]=nf[0]=1;
for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%Q;
nf[n]=qkw(fac[n],Q-2);
for(int i=n-1;i;i--) nf[i]=nf[i+1]*(i+1)%Q;
for(int i=1;i<=n;i++) s[i]=(s[i-1]+a[i])%Q;
}
signed main()
{
int T=fr();
n=fr(),q=fr();
for(int i=1;i<=n;i++) a[i]=fr();
prework();
while(q--)
{
l=fr(),r=fr(),p=fr();
int L=p-l,R=r-p,lim=min(L,R);
int res1=a[p],res2=qkw(((r-l)/2+1),Q-2);
for(int k=1;k<=lim;k++)
{
int t1=C(L-1,k-1)*C(R,k)%Q;
int t2=C(L,k)*C(R-1,k-1)%Q;
int t3=C(L,k)*C(R,k)%Q;
(res1+=( t1*(s[p-1]-s[l-1]+Q)%Q + t2*(s[r]-s[p]+Q)%Q + t3*a[p]%Q )%Q*qkw(t3,Q-2)%Q)%=Q;
}
ans^=res1*res2%Q;
}
fw(ans);
return 0;
}
我们需要消去每次 \(m\) 的影响,做到 \(O(q)\),发现该式可以约分!!!
对下式定义式展开
即 \(\frac{m}{L}\),求和即可,设 \(M=\min(L,R)\)
取模次数过多,预处理逆元,不然还带个 \(O(\log q)\)
\(O(q)\)
const int N=4e6+10,Q=998244353;
int n,q,l,r,k,ans;
int a[N],s[N],inv[N];
signed main()
{
int T=fr();
n=fr(),q=fr();
for(int i=1;i<=n;i++) a[i]=fr();
for(int i=1;i<=n;i++) s[i]=(s[i-1]+a[i])%Q;
inv[1]=1;
for(int i=2;i<=4e6+5;i++) inv[i]=((-(Q/i)*inv[Q%i])%Q+Q)%Q;
while(q--)
{
l=fr(),r=fr(),k=fr();
int L=k-l,R=r-k,M=min(L,R);
int res1=((s[k-1]-s[l-1]+Q)*M%Q*(M+1)%Q*inv[L*2]%Q+
(s[r]-s[k]+Q)*M%Q*(M+1)%Q*inv[R*2]%Q+(M+1)*a[k]%Q)%Q;
int res2=inv[(r-l)/2+1];
ans^=(res1*res2%Q);
}
fw(ans);
return 0;
}
T41 P2962 [USACO09NOV] Lights G
\(n \leq 35\)
考虑折半搜索,先预处理前一半灯所有情况,然后用 \(map\) 存到达这种状态的最小值,和后一半一拼就行了
每个点影响的点,用个 \(01\) 串状压存一下就行了
注意要用 \(1ll<<x\) 不用 \(1<<x\)
const int N=40;
int n,m,u,v,ans=LONG_LONG_MAX,T,lim;
int s[N];
map<int,int> reach;
void dfs(int now,int st,int val)
{
if(val>=ans) return;
if(!reach.count(st)) reach[st]=val;
else reach[st]=min(reach[st],val);
if(reach.count(T^st) || st==T) ans=min(ans,reach[T^st]+val);
if(now==lim+1) return; //在这里return 在上面的话状态没搜完
dfs(now+1,st,val);
dfs(now+1,st^s[now],val+1);
}
signed main()
{
n=fr(),m=fr();
for(int i=1;i<=m;i++)
{
u=fr(),v=fr();
s[u]|=(1ll<<v),s[v]|=(1ll<<u);
}
for(int i=1;i<=n;i++)
s[i]|=(1ll<<i),T|=(1ll<<i); //1ll
lim=n>>1,dfs(1,0,0);
lim=n,dfs((n>>1)+1,0,0);
fw(ans);
return 0;
}
T42 P7883 平面最近点对(加强加强版)
首先按 \(x\) 排序
我们可以接受 \(O(n\log n)\) 的复杂度
考虑分治算,按 \(x\) 作为 \(mid\) 递归处理
设 \(solve(l,r)\) 表示处理 \([l,r]\) 内的点的点对最小距离
我们已知 \([l,mid]\) 和 \([mid+1,r]\) 的答案,我们现在只用考虑跨过 \(mid\) 的点对
设 \([l,mid]\) 和 \([mid+1,r]\) 答案较小值为 \(k\)
我们只用管 \(fabs(x-mid) \leq \sqrt k\) 的点
这个时候我们再按 \(y\) 排序,每次找出左边哪些点可能成为线段左端点和右边的可能点
然后枚举左右点即可
这样做看似 \(O(n^2)\) 但是如果两个点的 \(y\) 值差 \(\gt k\) 也不可能成为答案
这样的点只可能有 \(6\) 个见下图,所以是线性的,双指针做一下即可
注意判断两点重合的情况,输入判断即可
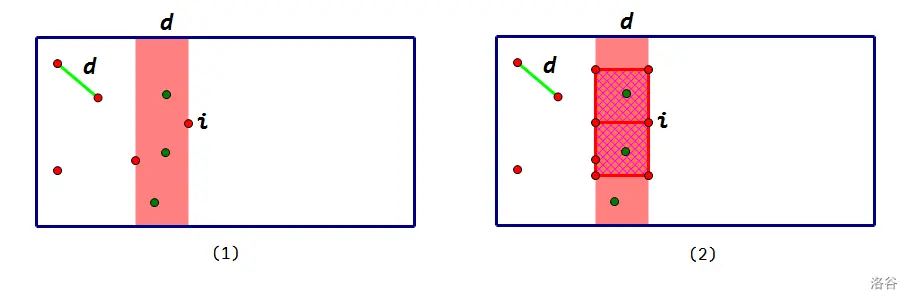
注:要开方一个小 \(trick\) 最后再开方
注意 \(x\) 恰好在中线的情况,这种直接暴力左边右边都加,然后后面算距离的时候判断是否相等即可,这样写还要在输入的时候判断下有没有重合的点
in_merge 函数 http://c.biancheng.net/view/7485.html
const int N=4e5+10;
int n,inf=1e18;
struct node{
int x,y;
bool operator<(const node&Q)const{
return (x==Q.x)?(y<Q.y):(x<Q.x);
}
bool operator!=(const node&Q)const{
return (x!=Q.x || y!=Q.y);
}
}dot[N],ans[N],lq[N],rq[N];
int sqr(int x){return x*x;}
int d(node a,node b){return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);}
void merge(int l,int r)
{
int x=(l+r)>>1;
int k=0,i=l,j=x+1;
while(i<=x && j<=r)
{
if(dot[i].y<=dot[j].y) ans[k++]=dot[i++];
else ans[k++]=dot[j++];
}
while(i<=x) ans[k++]=dot[i++];
while(j<=r) ans[k++]=dot[j++];
for(int i=l,j=0;i<=r;i++,j++) dot[i]=ans[j];
}
int solve(int l,int r)
{
if(l>=r) return inf;
if(l+1==r)
{
if(dot[l].y>dot[r].y) swap(dot[l],dot[r]);
return d(dot[l],dot[r]);
}
int mid=(l+r)>>1,line=dot[mid].x;
int k=min(solve(l,mid),solve(mid+1,r)),res=k,s=sqrt(k)+1;
merge(l,r);
int lf=0,rt=0;
for(int i=l;i<=r;i++)
{
if(dot[i].x==line) lq[++lf]=dot[i],rq[++rt]=dot[i];
else if(dot[i].x<line && sqr(dot[i].x-line)<k) lq[++lf]=dot[i];
else if(dot[i].x>line && sqr(dot[i].x-line)<k) rq[++rt]=dot[i];
}
for(int i=1,j=1;i<=lf && j<=rt;i++)
{
while(rq[j].y<lq[i].y-s && j<=rt) j++;
for(int t=j;rq[t].y<=lq[i].y+s && t<=rt;t++)
if(lq[i]!=rq[t]) res=min(res,d(lq[i],rq[t]));
}
return res;
}
signed main()
{
n=fr();
for(int i=1;i<=n;i++) dot[i].x=fr(),dot[i].y=fr();
sort(dot+1,dot+1+n);
for(int i=1;i<n;i++)
if(dot[i].x==dot[i+1].x && dot[i].y==dot[i+1].y) {puts("0");return 0;}
fw(solve(1,n));
return 0;
}
T43 P3066 [USACO12DEC]Running Away From the Barn G
显然有暴力的 \(O(n^2)\)
发现这个距离随着点的下降是单调,考虑一个子节点对父亲的贡献
在子节点 \(x\) 和一个 \(dis \leq t\) 的父亲之间这条路径上的点全部都可以 \(++\),树上路径问题,考虑树上差分做
考虑当前处理的点为 \(x\),把它上方的父亲全部丢到栈里,维护一个指针指向最上层的父亲,恰好距离 \(\leq t\) 即可,然后做一遍树上差分
每次遍历到 \(x\),就把节点 \(x\) 加入栈,自己结束递归上传的时候再 \(top--\),这样就可以保证栈里面只有自己的父亲和自己
判断距离就维护到根的距离
因为差分是在点上的,所以栈的指针移动的时候,我们还要减去边权,这里就是常见的 \(trick\) 父亲到儿子边权记在儿子上(因为父亲数 \(\leq 1\))
还可以先倍增预处理,然后暴力跳父亲
const int N=2e5+10;
int n,p,u,w,t,top;
int d[N],f[N],ak[N],fa[N],val[N];
vector<pi> as[N];
void dfs(int x,int lt,int s)
{
ak[++top]=x;
while(s>t) s-=val[ak[++lt]]; //指针移动 因为这条边在儿子上所以先 ++
d[x]++,d[fa[ak[lt]]]--; //ak[lt] 满足要求 做差分在父亲上
go(it)
{
int v=it.first,len=it.second;
dfs(v,lt,s+len);
}
top--;
}
int calc(int x)
{
int res=d[x];
go(it) res+=calc(it.first);
return f[x]=res;
}
signed main()
{
n=fr(),t=fr();
for(int i=2;i<=n;i++)
fa[i]=p=fr(),val[i]=w=fr(),as[p].pb({i,w});
dfs(1,1,0);
calc(1);
for(int i=1;i<=n;i++) fw(f[i]),nl;
return 0;
}
倍增代码,懒得写了贴个别人的
struct Tree
{
void get_fa(int x) { for(int i = 1;i <= 19;i ++) fa[x][i] = fa[fa[x][i - 1]][i - 1];}
inline void work(int x)
{
val[x] ++; ll tmp = l;
for(int i = 19;i >= 0;i --) if(dis[x] - dis[fa[x][i]] <= tmp) tmp -= dis[x] - dis[fa[x][i]] , x = fa[x][i];
if(x != 1) val[fa[x][0]] --;
}
inline void LOL()
{
n = read(); l = read(); fa[1][0] = 1;
for(int i = 2;i <= n;i ++) fa[i][0] = read() , dis[i] = dis[fa[i][0]] + read() , get_fa(i);
for(int i = 1;i <= n;i ++) work(i);
for(int i = n;i > 1;i --) val[fa[i][0]] += val[i];
for(int i = 1;i <= n;i ++) printf("%d\n",val[i]);
}
}DNF;



 浙公网安备 33010602011771号
浙公网安备 33010602011771号