图论
连通性
强连通分量
定义
强连通: 在有向图中, \(u\) 、\(v\) 两点之间存在从 \(u\) 到 \(v\) 的路和从 \(v\) 到 \(u\) 的路,我们称 \(u\) , \(v\) 强连通。
强连通图 :在有向图中, 任意两点均为强连通,那么这个图称强连通图,我们认为单个节点的图不是强连通图。
强连通分量(SCC) :在非强连通图中的极大强连通子图,我们认为单个节点的子图也是强连通分量,也就是说没有任意一个其他的强连通子图将他包含。
Tarjan 算法
在算法中,我们定义一下几个变量和维护信息。
栈 \(t\) :维护当前搜索信息。
\(dfn_u\) : DFS 时搜索到的次序。
\(low_u\) : \(u\) 可以搜索到在 \(t\) 中最早入栈的节点。
\(vis_u\) : \(u\) 是否在栈里过(1为在,0为不在)。
DFS 生成树
我们在进行DFS的时候,利用搜索顺序,来建一棵树,此树并非正常的树,这棵树由四种边组成。
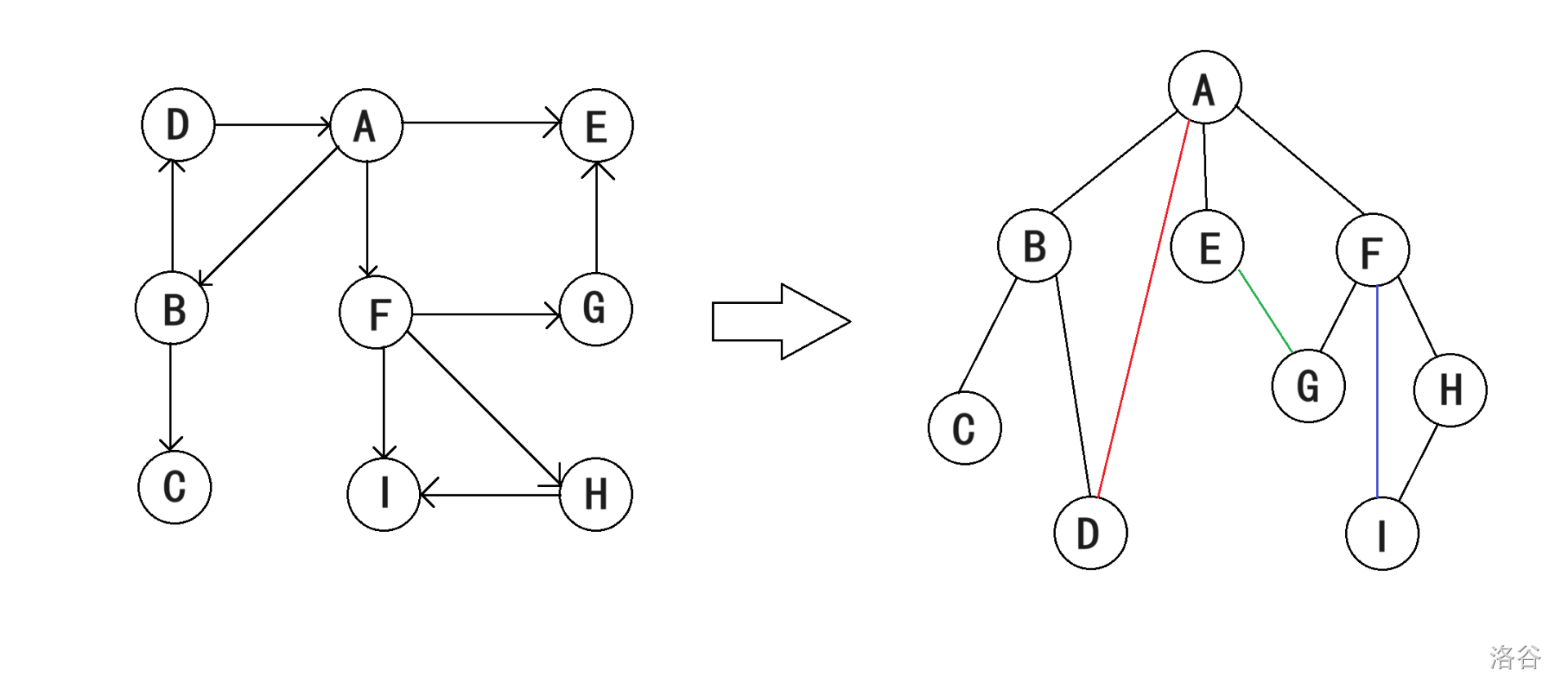
如上图,将一个有向图转化成了一个DFS生成树,根为A,其包含以下四种边:
树边:正常树的边,黑色部分,方向由根节点往下,如A指向B,B指向C,在搜索中找到一个新的节点所指向的边。
返祖边:指向到祖先节点的边,红色部分,由D指向A,在搜索中找到已经访问过的该节点的祖先节点,不一定要返回根节点。
横叉边:指向已经访问过的节点的边,绿色部分,由G指向E,该节点一定不是其祖先或父节点,也就是他们两的最近公共祖先是其他点,在搜索中找到已经访问过的边。
前向边:指向当前节点子树已经返回过的节点,蓝色部分由F指向I,在搜索找到已经访问过的当前子树的点,所以F到I一定在F到H之后遍历。
算法流程
该算法可以由任意节点开始,我们从 A 开始。
步骤如下:
$1 $ .从根节点开始搜索,维护 \(dfn\) 与 \(low\) 。
$2 $ .每搜索到一个点, \(vis_u=1,dfn_u=id,low_u=dfn_u\) ,\(id\) ,为DFS搜索到的次序,将该点入栈。
$3 $ .若该节点是 \(u\) ,下一个访问到的节点是 \(v\) ,那么有:
$ A $.若 \(v\) 没有被访问(树边),对 \(v\) 进行 2操作 ,在递归回溯时,更新 \(low_u=\min(low_u,low_v)\) ,也就是说如果 \(v\) 能到达 \(dfn_x\) ,那么 \(u\) 也能到达。
$ B $.若 \(v\) 已经被访问且在栈里(返祖边或前向边),那么有 \(low_u=\min(low-u,dfn_v)\) ,为什么不用 \(low_v\) 更新?如果这是一条返祖边,那么实际上 \(low_v\) 会在递归回溯时才更新,所以没有意义,如果是一条前向边,那么实际上 \(dfn_v\) 会比 \(low_u\) 大,不用管他。
$ C $.若 \(v\) 已经访问且不在栈里(横叉边),说明他已经被当做一个强连通分量处理,不用管它
\(4\).当前节点结束全部递归回溯后 ,如果 \(dfn\) 与 \(low\) 相等,那么当前节点的子树就是一个强连通分量,将其元素全部出栈。
证明:为什么只要判断这个就行了?因为强连通的每一对点对都可以互相抵达。如果当前子树是一个合法的强联通分量,那么当前以节a点为根的子树所有 \(dfn_u<dfn_v\) 的 \(u\),\(v\) 中,\(u\) 可以单向到达 \(v\) ,根节点可以单向到达所有节点,那么所有叶子节点(排除已经访问且出栈的节点)都要有一条指向 \(dfn_x>dfn_a\) 的返祖边,这是后通过 3.b 就会更新其 \(low\) ,再递归回去,此时在更新沿路所有节点的 \(low\) ,直到出现 \(dfn_x=low_x\) 。如果叶子节点没有返祖边,那么回溯到叶子节点时,就会触发 \(dfn_x=low_x\) 算一次强连通分量。
我们对于上图进行一下模拟:
1.搜索到 A, \(dfn_A:=low_A:=1,vis_A:=1,t.puah(A)\);
2.搜索到 B, \(dfn_B:=low_B:=2,vis_B:=1,t.push(B)\);
3.搜索到 C, \(dfn_C:=low_C:=3,vis_C:=1,t.push(C)\);
4.回溯到 C, \(dfn_C=low_C,t.pop(),vis_C:=0\) ,强连通分量更新;
5.搜索到 D, \(dfn_D:=low_D:=4,vis_D:=1,t.push(D)\);
6.搜索到 A, \(vis_A=1\) ;
7.回溯到 D, \(low_D:=\min(dfn_A,low_D)=1\);
8.回溯到 B, \(low_B:=\min(low_B,low_D)=1\);
9.回溯到 A, \(low_A:=\min(low_A,low_B)=1\);
10.搜索到 E,\(dfn_E:=low_E:=5,vis_E=1,t,push(E)\);
11.回溯到 E,\(dfn_E=low_E,t.pop(),vis_E=0\) ,强连通分量更新;
12.回溯到 A,\(low_A:=\min(low_A,low_E)=1\);
13.搜索到 F,\(dfn_F:=low_F:=6,vis_F:=1,t.push(F)\);
14.搜索到 G,\(dfn_G:=low_G:=7,vis_G:=1,t.push(G)\);
15.搜索到 E,\(vis_E=0\),返回;
16.回溯到 G,\(dfn_G=low_G,t.pop(),vis_G=0\) ,强连通分量更新;
17.回溯到 F,\(low_F:=\min(low_F,low_F)=6\);
18.搜索到 H,\(dfn_H:=low_H:=8,vis_H:=1,t.push(H)\);
19.搜索到 I,\(dfn_I:=low_I:=9,vis_I:=9,t.push(I)\);
20.回溯到 I,\(dfn_I=low_G,t.pop(),vis_G=0\) ,强连通分量更新;
21.回溯到 H,\(low_H:=\min(low_H,low_I)=8,dfn_H=low_H,t.pop(),vis_H=0\) ,强连通分量更新;
22.回溯到 F,\(low_F:=\min(low_H,low_F)=7,dfn_F=low_F,t.pop(),vis_F=0\) ,强连通分量更新;
23.回溯到 A,\(low_A:=\min(low_A,low_F)=1,dfn_A=low_A,t.pop(),vis_A=0\) ,强连通分量更新;
最终强连通分量更新为 23 A的子树,点集 \({A,B,D}\) 。
在实际操作中, \(pop\) 一定要将改点的子树全部 \(pop\) 干净,更新时要附带一些信息,当前点集,当前强连通分量的长度。
vector<int>g[N];
int dfn[N],low[N],id,top,stk[N],cnt,scc[N];//scc记录节点属于哪个强连通分量
bool vis[N];
void Tarjan(int u) {
dfn[u]=low[u]=++id;
vis[u]=1,stk[++top]=u;
for (int v : g[u]){
if (!dfn[v])Tarjan(v),low[u]=min(low[u],low[v]);
else if(vis[v])low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]) {
cnt++;
int tmp=-1;
while(u!=tmp) {
tmp=stk[top--];
scc[tmp]=cnt;
vis[tmp]=0;
}
}
}
割点与桥
定义
如果在无向图中,点 \(u\) ,\(v\) 之间有一条路径,称他们连通,如果一个图中,任意的 \(u\) ,\(v\) 都连通,那么这是个连通图。
非连通图的极大连通子图为连通分量,即没有被其他的连通子图包含的连通子图。
如果在无向图中,如果 删除该点 ,可以增加图的连通分量,那么这个点就是割点。
如果在无向图中,如果 删除该边 ,可以增加图的连通分量,那么这个边就是割边。
Tarjan 算法
没错,还是他,还是DFS生成树。
割点
我们知道,Tarjan 算法是通过对搜索顺序生成一个DFS生成树。
我们又知道,DFS生成树是有方向的。
我们还知道,无向图是无相的。
但是,经过简单的推理,我们发现,如果点 \(u\) 是一个割点,那么其所有邻居有且只有经过该点才能到达其他的点。
(无向图没有横叉边)
所以我们和之前的Tarjan一样,维护一个 \(dfn\) ,与 \(low\) 。
从任意根节点开始搜索。
我们将搜索到的边定义为有向的,然后与之前一样,找返祖边,当且仅当若 \(u\) 的任意子节点是 \(v\) ,且 \(dfn_u\le low_v\) ,那么 \(u\) 为割点。
证明:为什么要把无相边定义成有向边?我们知道 ,\(u\) 为一个割点,那么其子节点一定不能再到 \(u\) ,即没有返祖边到 \(u\) ,我们设 \(x\) 为 \(u\) 的祖先, \(y\) 为 \(u\) 的后代,如果从 \(x\) 到 \(y\) 的路径可以不经过 \(u\) ,那么 \(u\) 点即使删了,也不会影响 \(x\) , \(y\) 的连通,只要有一个子节点没有返祖边到 \(u\) 的祖先,那么该节点只能经过 \(u\) 节点,删掉 \(u\) 就影响其连通性,所以 \(u\) 为割点,记录的 \(low\) 就是最远能返回的祖先节点,如果有子节点的 \(low\) 小于 \(dfn_u\) ,那么其必须经过 \(u\) 才能到达祖先节点,所以 \(u\) 为割点。
对于根节点,如果其有大于两个的子节点,那么也是割点。
int dfn[N], low[N], tot;
bool f[N], ans[N];
vector<int> g[N];
void dfs(int u, int rt) {
dfn[u] = low[u] = ++tot, f[u] = 1;
int c = 0;
for (int v : g[u]) {
if (!dfn[v]) {
c++, dfs(v, rt), low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u] && u != rt) ans[u] = 1;
} else low[u] = min(low[u], dfn[v]);
}
if (u == rt && c >= 2) ans[u] = 1;
}
桥
其实只要将 \(dfn_u\le low_v\) 改为 \(dfn_u<low_v\) 原理一样,但是如果刚好到该节点,那么割该节点连接子节点的边毫无意义。
int dfn[N], low[N], tot;
vector<int> g[N], bridge;
void dfs(int u, int fa) {
dfn[u] = low[u] = ++tot;
bool flag = 0;
for (int v : g[u]) {
if (!dfn[v]) {
c++, dfs(v, u), low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) flag = 1;
} else if (v != fa) low[u] = min(low[u], dfn[v]);
}
if (flag) bridge.push_back({fa, u});
}
拓扑排序
在生活中,处理一些事情是要分先后顺序的,比如你想吃饭就得先到食堂,向到食堂就得先下课...我们将这些事情转化成一张有向图,连接 \(u\) 到 \(v\) 的有向边,代表做 \(v\) 之前,就得先做 \(u\) ,有时候做一件事需要先做完多件事,我们把这个值叫做入度,即指向该节点的边的数量,有时候做完一件事后会满足多件事的条件,我们把这个值叫出度,即有该节点出发的数量,做事情的次序就是拓扑序,做事情的过程就是拓扑排序的过程。
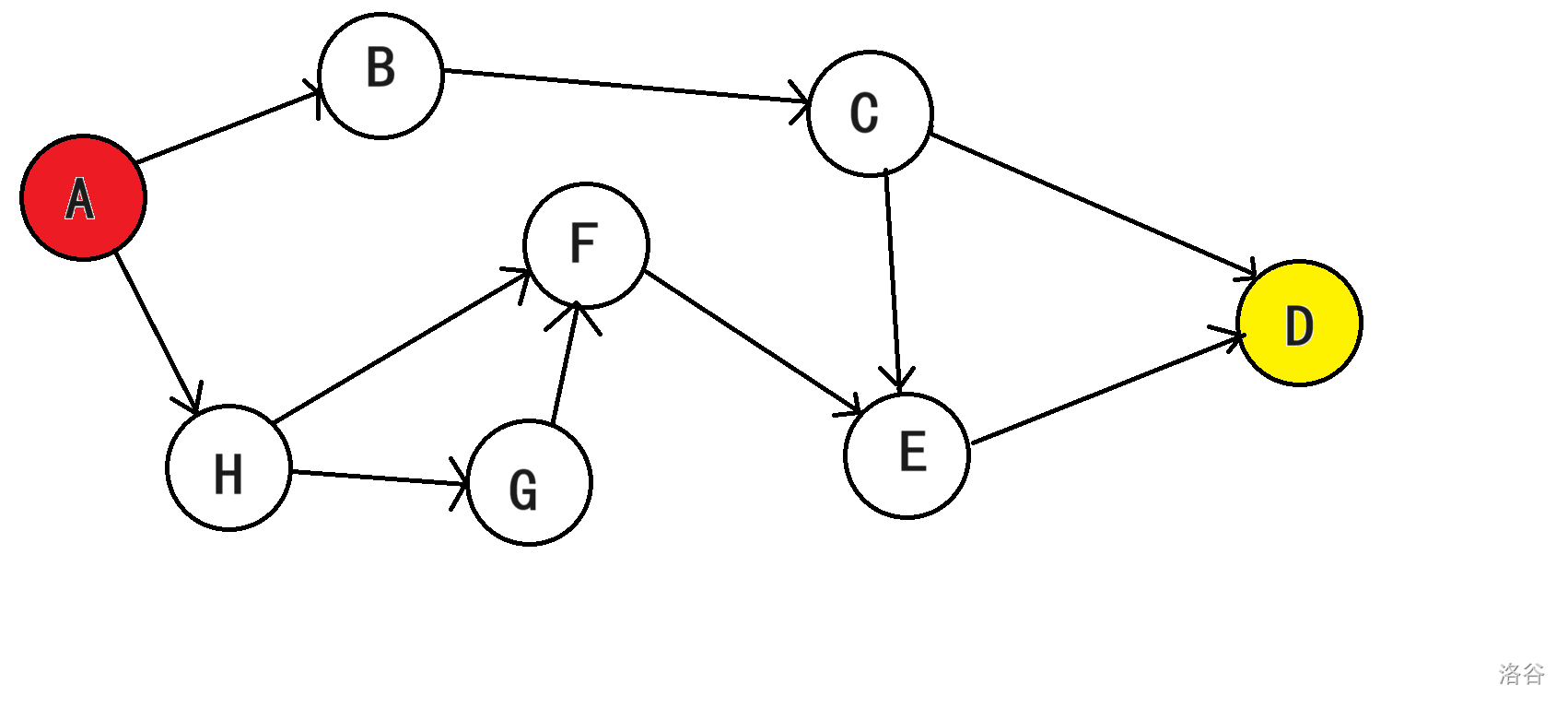
在上图中标红的点A的入度为0,没有节点会影响A的次序。
标黄的点B的出度为0,他的次序不会影响到任何节点。
只有在当前节点入度为0的时候,才可使用该点,存到拓扑序中,当该点已经存在拓扑序中时,他的出边连接的点的入度-1。
我们模拟一下:
1.初始节点是入度为0的A,将他存入拓扑序中,B,H入度-1;
2.B此时的入度为0,将他存进去,C入度-1;
3.C此时的入度为0,将他存进去,D,E入度-1;
4.H此时的入度为0,将他存进去,G,F入度-1;
5.G此时的入度为0,将他存进去,F入度-1;
6.F此时的入度为0,将他存进去,E入度-1;
7.E此时的入度为0,将他存进去,D入度-1;
2.D此时的入度为0,将他存进去,拓扑排序结束。
最终拓扑序为:ABCHGFED
拓扑序数量可能不为1。
如果这个有向图中有环,那么无法拓扑排序,由于环到存在,一些节点的入度会一直为1 。
比如:莲藕越大,洞越多,洞越多,莲藕越小,所以莲藕越大莲藕越小。
这种成环的子图是不可取的,他们互相是对方的出度和入度,所有只有有向无环图才能实现拓扑排,所有有向无环图都能实现。
我们用一个队列实现,现将入度为0的节点全部入队,接着一个个取出,遍历其指向的节点,遍历到的使入度-1,如果该节点入度为0,那么入队。同样也可以让出度为0的入队,那么需要反向建图,会得到一个逆序的拓扑序。
一般我们会要得到字典序最小的拓扑序,所以只要将队列改为优先队列就行,复杂度 \(O(m+n\log n)\) , \(n\) 为点数, \(m\) 为边数。
vector<int>g[N],ans;
int r[N];//按入度排序,只记录入度
void tp_sort(){
priority_queue<int>q;
for(int i=1;i<=n;i++)
if(r[i]==0)q.push(i);
while(!q.empty){
int u=q.top();
q.pop;
ans.push_back(u);
for(int i=0;i<g[u].size();i++){
r[g[u][i]]--;
if(r[g[u][i]]==0)q.push(g[u][i]);
}
}
}
拓扑排序判环
只要在此基础上定义一个 \(vis\) 记录是否被排到,如果有环,那么其入度永远不为0,无法排到。
vector<int>g[N],ans;
int r[N];
bool vis[N]
void tp_sort(){
priority_queue<int>q;
for(int i=1;i<=n;i++)
if(r[i]==0)q.push(i);
while(!q.empty){
int u=q.top();
q.pop;
ans.push_back(u);
vis[u]=1;
for(int i=0;i<g[u].size();i++){
r[g[u][i]]--;
if(r[g[u][i]]==0)q.push(g[u][i]);
}
}
for(int i=1;i<=n;i++)
if(!vis[i]){
cout<<"NO!";
return;
}
}
欧拉图
定义
欧拉通路:每条边恰好经过一次的通路。
欧拉回路:每条边恰好经过一次的环路(头尾相接)。
半欧拉图:具有欧拉通路但不具有欧拉回路的图。
欧拉图:具有欧拉回路的图。
性质
无向图
如果所有点的度数都是偶数(下文简称偶数点),那么他就是一个欧拉回路。
如果有且仅有两个点是奇数(下文简称奇数点),那么他就是一个欧拉通路。
图中奇数点的数量总是成对出现。
对于欧拉图,无论从哪一点出发,总是能走出一个完整的欧拉回路。
对于半欧拉图,只有从两奇数点之一出发,从另一点结束,才能走出一个欧拉通路。
有向图
如果所有点的入度与出度之差为0,那么他就是一个欧拉回路。
如果有且仅有两点的入度与出度之差为1与-1,那么他就是一个欧拉通路。
图中所有点入度与出度之差和为0。
对于欧拉图,无论从哪一点出发,总是能走出一个完整的欧拉回路。
对于半欧拉图,只有从出度1的那个点走到入度多1的那个点,才能走出一个欧拉通路。
Hierholzer求欧拉路
流程
选取一个点作为起点,遍历其边,回溯时将其放入栈中,再输出栈。
如果要求字典序最小,那么排一下边的顺序就行。
stack<int>t;
vector<int>g[N];
bool vis[N][N];
void dfs(int u){
for(int i=0;i<g[u].size();i++){
if(vis[u][g[u][i]]==0){
vis[u][g[u][i]]=1;
dfs(g[u][i]);
}
}
t.push(u);
}
最短路
定义
两点之间的最短路径长度(或权值)
约定
我定义一下变量
\(n\) 是图的点数,\(m\) 是图的边数。
\(w\) 是点 \(u\) 到点 \(v\) 的权值。
\(s\) 最短路的起点。
Floyd
这是所有最短路中最简单的算法了。
Floyd其实就是dp。
我们定义一个状态 \(dp_{i,j,k}\) 表示只经过节点 \(1~k\) 组成的子图的路径的 \(i,j\) 之间最短路。
那么有状态转移
意思是你通过 \(1~k\) 的子图从 \(i\) 走到 \(j\) ,等于你通过 \(1~k\) 的子图从 \(i\) 走到 \(k\) 再走到 \(j\) 。
我们发现第一维只与 \(k-1\) 有关,那么可以自己递推自己,省略掉第一维,此时 $$dp_{i,j}=\min(dp_{i,k},dp_{i,k},dp_{k,j})$$
现在我们写出三层循环,计算 \(dp\) ,注意 \(k\) 一定是最外层,因为已经被优化了,所以优先枚举,不然会覆盖。
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int k=1;k<=n;k++)
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
我们发现计算完成之后 \(dp\) 数组存的是所有点对之间的最短路,所以也称 多源最短路 复杂度 \(O(n^3)\) 。
常用于多次询问最短路的题,提前算出Floyd, \(O(1)\) 查询。
但处理复杂度是在有点感人,并且有些题只要求一个点对之间的最短路,于是就有了另外两种求单源最短路的算法。
Dijkstra
Dijkstra(下文简称 dij)算法十分常用,复杂度高效,十分稳定,唯一缺点是不能处理负边权图。
dij 用于处理单源最短路,即点源点到其他点的最短路。
定义: \(dis_i\) 为 \(s\) 到 \(i\) 的最短路,优先队列 \(q\)(按 \(dis\) 从小到大),\(vis_i\) 标记 \(i\) 是否入过队。
其步骤如下:
- 将 \(dis\) 初始化为无穷大,\(vis\) 初始化为 \(0\) ,将 \(s\) 节点入队,标记 \(vis_s=1\) 。
- 将 \(q\) 的队头 \(u\) 出队,若 \(vis_u=1\) ,跳过这个节点;若 \(vis_u=0\) ,标记 \(vis_u=1\) ,遍历到其邻居 \(v\) ,如果 \(dis_u+w<dis_v\) ,则更新 \(dis_v=dis_u+w\) ,将 \(v\) 入队
- 若队列不为空,重复 2 的操作;若队列为空,则说明每一个节点都应被计算过,此时检查 \(vis\) 的标记,当有 \(vis_u\) 未被标记过时,则此图不连通,\(s\) 无法到达 \(u\) 。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m;
struct add{
int v,w;
};
vector<add>g[N];
int vis[N],dis[N];
struct node{
int u,dis;
friend bool operator<(node a,node b){
return a.dis>b.dis;
}
};
priority_queue<node>q;
void dij(int s){
for(int i=1;i<=n;i++)dis[i]=1e9+7;
dis[s]=0;
q.push((node){s,0});
while(!q.empty()){
int u=q.top().u;
q.pop();
if(vis[u]==1)continue;
vis[u]=1;
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v;
int w=g[u][i].w;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
q.push((node){v,dis[v]});
}
}
}
}
int main(){
int s;
cin>>n>>m>>s;
for(int i=1;i<=m;i++){
add a;
int b;
cin>>b>>a.v>>a.w;
g[b].push_back(a);
}
dij(s);
for(int i=1;i<=n;i++){
cout<<dis[i]<<" ";
}
return 0;
}
SPFA
它早死得透透,除非负环负负得正。
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+5;
struct node{
int v,w;
};
vector<node>g[N];
int n,m;
int dis[N],vis[N];
void spfa(int s){
queue<int>q;
for(int i=1;i<=n;i++)dis[i]=2147483647;
dis[s]=0;
vis[s]=1;
q.push(s);
while(!q.empty()){
int u=q.front();
q.pop();
vis[u]=0;
for(int i=0;i<g[u].size();i++){
int v=g[u][i].v;
int w=g[u][i].w;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
if(vis[v]==0){
vis[v]=1;
q.push(v);
}
}
}
}
}
int main(){
int s;
cin>>n>>m>>s;
for(int i=1;i<=m;i++){
int u;
node a;
cin>>u>>a.v>>a.w;
g[u].push_back(a);
}
spfa(s);
for(int i=1;i<=n;i++){
cout<<dis[i]<<" ";
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号