动态规划
简介
动态规划,简称动规、 \(dp\) ,俗称「的坡」。
所谓动规,要满足以下条件:
最优子结构:将整个大的问题变为子问题,在子问题中找到最优解,之后递推出整个问题。
无后效性:即前面的决策不影响后面。
重叠子问题:反复求解子问题,这时我们将他们存储起来,以免重复算。
基本dp
dp步骤
dp大致分为一下三步。
1.寻找最优子结构,
2.将最优子结构设置为dp状态,如 \(dp_{i,j}\) 表示从 \(i\) 到 \(j\) 的最大值。
3.推状态转移方程,也就是递推公式,可以从两个角度考虑,从当前的状态往后退,或通过前边的结果计算当前的,怎么方便怎么来。
这样,你就差不对将 \(dp\) 做出来了。
这看似很复杂,实际也不简单。
所以我们从简单的开始。
例题
P1216
如题,直接走下一个大的数字肯定不行。7->8->1->4->6显然小一点,那么就用dp来做。
我们可以这么想,如果当前节点的上面两个节点记录的是最优解,那么该节点继承大的。
如何维护最优解?
我们定义\(dp_{i,j}\)表示走到第\(i\)行\(j\)列的最优解,那么有状态转移式 \(dp_{i,j}=\max(dp_{i-1,j},dp{i-1,j-1})\) 。
对于 \(dp_{1,1}\) 的最大值就是他本身。
对于所有的 \(dp_{i,j}\) 我们将他设为原数组。
我们最后需要的答案,应该是最后一行的最大值,即\(dp_{n,j}\)
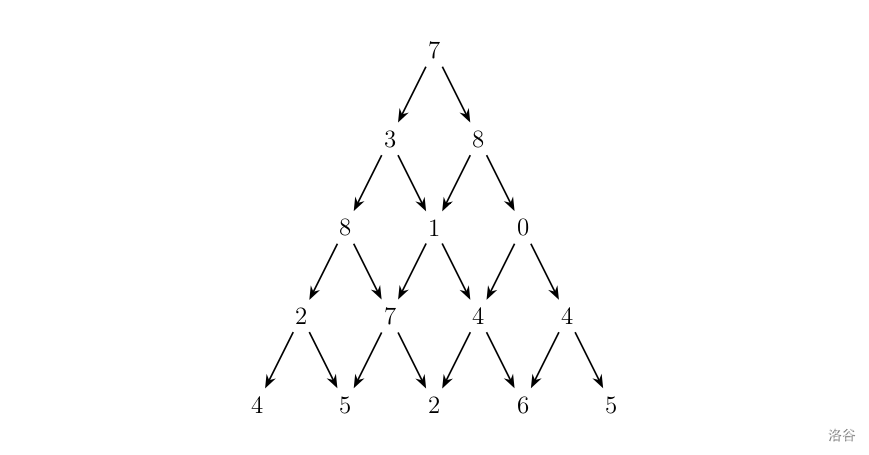
我们推一下。
\(dp_{1,1}=7\) ;
\(dp_{2,1}+=dp_{1,1}=10\) ;
\(dp_{2,2}+=dp_{1,1}=15\) ;
\(dp_{3,1}+=dp_{2,1}=18\) ;
\(dp_{3,2}+=\max(dp_{2,2},dp_{2,1})=16\) ;
\(dp_{3,3}+=dp_{2,2}=8\) ;
\(dp_{4,1}+=dp_{3,1}=20\) ;
\(dp_{4,2}+=\max(dp_{3,1},dp_{3,2})=25\) ;
\(dp_{4,3}+=\max(dp_{3,2},dp_{3,3})=20\) ;
\(dp_{4,4}+=dp_{3,3}=12\) ;
\(dp_{5,1}+=dp_{4,1}=24\) ;
\(dp_{5,2}+=\max(dp_{4,1},dp_{4,2})=30\) ;
\(dp_{5,3}+=\max(dp_{4,2},dp_{4,3})=27\) ;
\(dp_{5,4}+=\max(dp_{4,3},dp_{4,4})=26\) ;
\(dp_{5,5}+=dp_{4,4}=17\) ;
可见最大值 \(dp_{5,2}=30\) 。
对于边缘上的边,可以将其先算一遍,或从1开始,防止出界(注意初始化)。
完整代码。
#include<bits/stdc++.h>
using namespace std;
int dp[1005][1005],n,cnt;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cin>>dp[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
dp[i][j]+=max(dp[i-1][j],dp[i-1][j-1]);
}
}
for(int i=1;i<=n;i++){
cnt=max(cnt,dp[n][i]);
}
cout<<cnt;
return 0;
}
最长公共子序列
给定长度为 \(n\) 的序列 \(a\) 和长度为 \(m\) 的 \(b\) ,求出他们最长公共子序列的长度。 \(1\le n,m\le10^4\)
首先我们要知道,什么是最长公共子序列?
子序列是指将原序列中提取若干元素且不改变相对位置,可以理解为从原序列删除若干个元素后所剩下的序列;
公共子序列指他们共有的子序列;最长公共子序列就是其中最长的。
也就是说我们要分别从 \(a\) 和 \(b\) 中挑选 \(k\) 个元素并且不改变相对位置的情况下组成两个子序列,要求这两个子序列相同求 \(k\) 的最大值。
暴力
我们知道,对于每个元素都有选与不选两种情况,所以我们可以暴搜枚举,总复杂度是 \(O(2^n)\) 。
正解
我们设 \(dp_{i,j}\) 为只考虑 \(a\) 的前 \(i\) 项,只考虑 \(b\) 的前 \(j\) 项的最优结果。
接下来我们分情况讨论:
1 . 如果 \(a_i\) 与 \(a_j\) 相等,那么有 \(dp_{i,j}=\max(dp_{i-1,j-1}+1 , dp_{i,j})\) ,也就是说,如果选取 \(a_i\) 与 \(b_j\) ,那么当前长度等于选之前的 \(dp_{i-1,j-1}\) 加一。
2 . 如果不相等,有 \(dp_{i,j}=\max(dp_{i-1,j} , dp_{i,j-1})\) 也就是说继承没选是的最大值。
我们的答案就是 \(dp_{n,m}\) ,初始值 \(dp{0,0}=0\) 。
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(a[i]==b[j])dp[i][j]=max(dp[i-1][j-1]+1,dp[i][j]);
else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
最长上升子序列
现在有一个长度为 \(n\) 的序列 \(a\) ,选出一个子序列,使子序列中任意一个元素,其值都要比他前边的大。
题目中所描述的就是最长上升子序列,即一个升序的序列。
我们定义 \(dp_i\) 表示以 \(a_i\) 为结尾的上升子序列的长度。
那么 \(dp_1=1\) ,即序列就是他自己,对于所有的 \(dp_i\) 其最小长度就是自己,即 \(1\)。
我们可以这么想,在对 \(dp_i\) 进行运算时,可以将前面的所有已经算完的序列便利一遍,如果 \(a_j<a_i\) 说明一 \(j\) 结尾的最长上升子序列的末尾加上 \(a_i\) ,依旧是个合法的最长上升子序列,即以 \(i\) 为结尾的最长上升子序列长度等于以 \(j\) 结尾的加一。
最终答案就是所有 \(dp_i\) 之中最大的那个,注意不是 \(dp_n\) 因为这样的序列可能根本不存在。
dp[1]=1,ans=1;//即ans=dp[1]
for(int i=2;i<=n;i++){
dp[i]=1;
for(int j=1;j<i;j++)
if(a[i]>a[j])
dp[i]=max(dp[i],dp[j]+1);
ans=max(dp[i],ans);
}
背包
01背包
P1048
题意:有 \(m\) 珠草药,每珠草药有一个价值 \(a_i\) ,你需要花费 \(t_i\) 的时间去采集,总共有 \(T\) 的单位时间,求能采到的最大价值。
我们设 \(dp_{i,j}\) 为采前 \(i\) 珠草药并花费 \(j\) 的时间。
对于每一种草药,只有采与不采两种选择,如果不采,换到下一个 \(i\) 继续判断,如果采,那么 \(j\) 加上需要的时间。
我们枚举 \(i\) 与 \(j\) 如果不采,那么 \(dp_{i,j}=dp_{i-1,j}\) ,继承它上一个 \(i\) ,如果采 ,那么 \(dp_{i,j}=dp_{i-1,j-t_i}\) ,时间 \(j\) 维护的最优解应该是它采之前的最优解,即 \(j-t_i\) 。
接着,我们对以上结果取最大值,得到转移方程 \(dp_{i,j}=\max(dp_{i-1,j},dp_{i-1,j-t_i})\) 。
最后求得的结果就是 \(dp_{m,T}\) ,即采所有草药花费所有时间的最大值。
#include<bits/stdc++.h>
using namespace std;
int dp[1005][1005],m,T,a[1005],t[1005];
int main(){
cin>>T>>m;
for(int i=1;i<=m;i++){
cin>>t[i]>>a[i];
}
for(int i=1;i<=m;i++){
for(int j=1;j<=T;j++){
if(j>=t[i])
dp[i][j]=max(dp[i-1][j-t[i]]+a[i],dp[i-1][j]);
else dp[i][j]=dp[i-1][j];//只有当前枚举的时间能采才判断是否采,否则均不采,更新
}
}
cout<<dp[m][T];
return 0;
}
01背包的含义就是每个物品只有0,1两种状态,即取与不取。
一般是这样的题型:给你 \(n\) 个物品,他们的价值、空间(即代价,本题的时间),和一个总的空间,问这个空间里选取若干个数的最大值。
01背包优化
更具上文状态转移方程式,我们发现,对 \(dp_{i,j}\) 造成影响的只有 \(dp_{i-1,j}\) 和 \(dp_{i-1,j-t_i}\) ,观察第一维,实际上我们只需要维护 \(dp_{i-1}\) 的值,并且实际上 \(do_{i-1,j}\) 代表的是不取,对其值并没有改变,只是继承上一个而已,题目也对选第几个没有要求,所以我们可以把第一维优化掉。
for (int i=1;i<=n;i++)
for (int j=T;j>=t[i];j--)//注意,一定要从T开始,不然会被覆盖
dp[j]=max(dp[j],dp[j-t[i]]+a[i]);
这个操作也叫滚动优化。
多重背包
多重背包跟01背包很相似,只是每一个物体都能选择 \(k_i\) 此,因此在01背包的基础上,再添加一个 \(for\) ,枚举每个物品选取得的次数,转移方程就是
其中 \(c_i\) 代表空间, \(v_i\) 代表价值, \(k_i\) 是最多选取个数。
写成代码是这样子的:
for(int i=1;i<=m;i++){
for(int j=1;j<=T;j++){
for(int l=0;l<=k[i];l++){
if(j>l*c[i])
dp[i][j]=max(dp[i-1][j-l*c[i]]+v[i]*l,dp[i-1][j])
}
}
}
完全背包
完全背包就是每个物品都能选择无限次。
如果我们跟多重背包一样,取枚举个数,那么就是 \(O(n^3)\) 。
我们可以这样想,如果 \(dp_{i,j-c_i}\) 已经为前面的最大值,那么有 \(dp_{i,j}=\max(dp_{i,j-c_i}+v_i,dp_{i-1,j})\),复杂度 \(O(n^2)\) 。
为什么多重背包不行呢?因为,每一个物品都有他自己的上限,需要分开讨论,而完全背包混合在一起也无妨。
这时候我们发现,他跟01背包很相似,一样可以优化掉第一维。
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= a[i]) dp[i][j] += dp[i][j - a[i]];
}
}
分组背包
在有些题目中,我们选择的物品并不是在所有的之中选,而是将所有物品分为几组。
在01背包优化过的基础上,再加一维,表示组数。
for (int k = 1; k <= ts; k++) // 循环每一组
for (int i = m; i >= 0; i--) // 循环背包容量
for (int j = 1; j <= cnt[k]; j++) // 循环该组的每一个物品
if (i >= c[t[k][j]]) // 背包容量充足
dp[i] = max(dp[i],dp[i - c[t[k][j]]] + v[t[k][j]]); // 像0-1背包一样状态转移
区间dp
所谓区间dp,就是在区间上做dp
这是很经典的一道区间dp。
首先进行区间dp,要满足以下性质:
可以将两个或多个区间合并;
要将问题转化成能两两合并的形式;
在区间内枚举合并点,将其分为两个区间,通过两个区间求出该区间的值。
具体如下:
首先开两倍空间,破环成链。
我们设 \(dp_{i,j}\) 为区间 \([i,j]\) 的最优解,再在 \([i,j]\) 之间枚举合并点 \(k\) ,那么\(dp_{i,j}=dp_{i,k}+dp_{k+1,j}\) ,所有的区间dp都要有这一步操作,枚举合并点,再求值。
那么有:
其中 \(\max\) 代表最值,可替换, \(sum\) 函数为合并 \(i\),\(j\) 的代价,在本题中其代价就是 \(\sum_{l=i}^j a_l\) ,这个可以用前缀和 \(O(1)\) 算。
#include<bits/stdc++.h>
using namespace std;
const int INF=1e9+7;
int dp1[205][205],dp2[205][205],w[205],a[205],ans1=INF,ans2;
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
a[i+n]=a[i];
}
for(int i=1;i<=n*2;i++)w[i]=a[i]+w[i-1];
n*=2;//为方便将n*2
for(int len=2;len<=n;len++){//枚举长度
for(int i=1;i<=n-len+1;i++){//枚举左端点
int j=i+len-1;//求右端点
dp1[i][j]=INF;
dp2[i][j]=0;//初始化
for(int k=i;k<j;k++){//枚举合并点
dp1[i][j]=min(dp1[i][j],dp1[i][k]+dp1[k+1][j]+(w[j]-w[i-1]));
dp2[i][j]=max(dp2[i][j],dp2[i][k]+dp2[k+1][j]+(w[j]-w[i-1]));
}
}
}
for(int i=1;i<=n/2;i++){//求最值,注意破环后i~i+(n/2)才是原环的循环节位置
ans1=min(ans1,dp1[i][(n/2)+i-1]);
ans2=max(ans2,dp2[i][(n/2)+i-1]);
}
cout<<ans1<<'\n'<<ans2;
}
树形dp
有些dp是在一棵树上进行的,这些就被称为树形dp。
树形dp的与众不同
树形dp与上文的所有dp最大的不同,就是在dp形式上进行了改变。
众所周知,树的各项运算求解的依赖于搜索,所以dp就不在是一个简单的循环,而是要边搜索,边进行dp。
大多树形dp的状态也发生改变, \(dp_i\) 一般都是表示 \(i\) 节点的状态。
转移方程更多的是表现父子节点的关系。
例题与实现
P1352
如题:有一颗 \(n\) 个节点的树,每个点有一个点权,如果节点 \(u\) 参加了舞会,那么节点 \(u\) 的所有子节点将不会参加。
我们分情况讨论:
1.如果节点 \(u\) 没参加,那么其任意子节点 \(v\) 有两种选择,参加或不参加。
2.如果节点 \(u\) 参加了,那么其任意子节点 \(v\) 不可能参加。
我们设 \(dp_{u,k}\) 表示根节点为 \(u\) 的子树的最大值, \(k\) 为其是否参加,参加为\(1\) ,不参加为 \(0\) 。
那么状态转移就是:
其中 \(l\) 代表 \(u\) 的子节点点集的长度,即遍历整个点集, \(a_u\) 代表节点 \(u\) 的贡献。
void dfs(int u){
dp[u][1]=a[u];//一开始选该点初始值为权值
for(int i=0;i<g[u].size();i++){//遍历子节点点集
dfs(g[u][i]);//递归
dp[u][0]+=max(dp[g[u][i]][1],dp[g[u][i]][0]);
dp[u][1]+=dp[g[u][i]][0];//一定要回溯后更新
}
}
注意,本题没有给定根节点,需要自己提前找出来,只要找到没有当过子节点的节点就行, \(dfs\) 从根开始计算,最后要对选与不选取最大值。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号