树状数组

简介

树状数组支持 \(O(\log n)\)的区间查询以及单点修改，对于区间修改是劣于线段树的，\(O(n\log n)\)，但是他码量比线段树少，常数小，并且可以应对题目卡常等问题。

基本思想与实现

区间维护

树状数组就是维护区间和，如图。

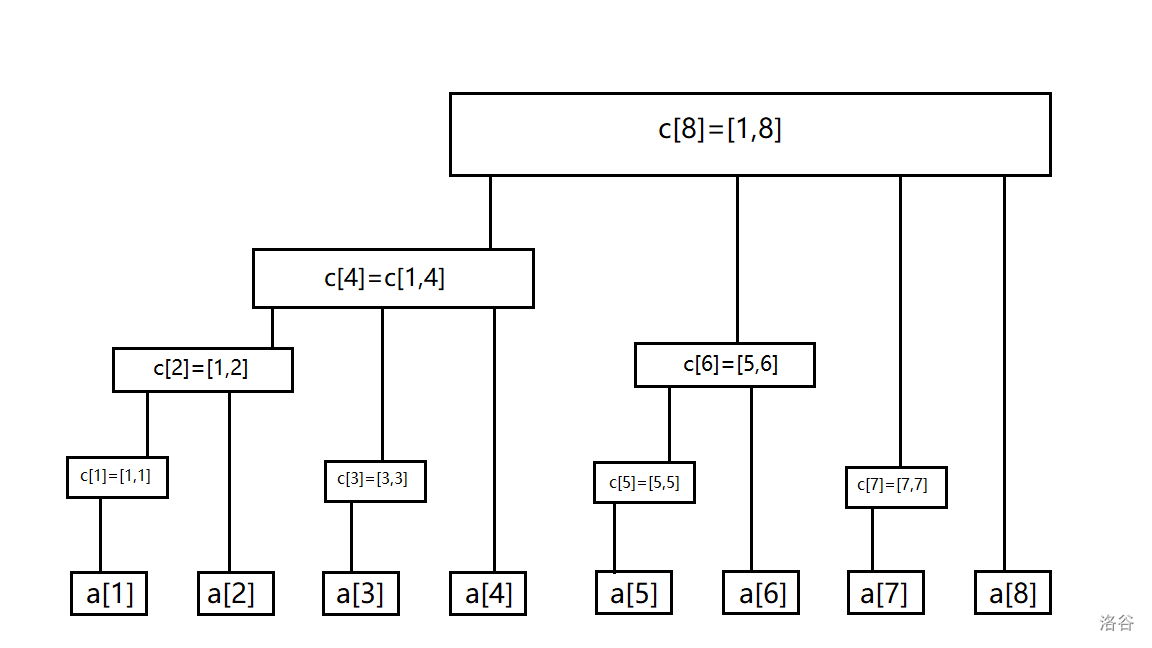
上图 \(c[i]\) 维护一定范围的区间和，那么如何知道维护哪一段的区间和呢？
我们打个比方比如说 \(4\) 将其转化成二进制得 \(100\)，维护长度为 \(4\) 的区间， \(6\) 转化成二进制得 \(110\) 维护长度为 \(2\) 的区间。
我们发现，维护的区间长度就是将其转化成二进制的最低位的 \(1\) 的权值，对于任何数均满足。我们将其记作 \(lowbit(i)\) ，那么整个 \(c[i]\) 的维护范围就是 \([i-lowbit(i)+1,i]\) 。
求这个函数是 \(O(1)\) 的，运用一些简单的位运算即可，完整函数如下：

lowbit(int i){return i&-i;}

我们来推导一下：
首先我们知道， \(-x\) 一定是负数，负数的二进制等于原码取反加一，我们令 \(k\) 为 \(a\) 的最低位，首先，在 \(k\) 的前面包括 \(k\) 的都会取反那么 \(k\) 前面的&运算都为0，\(k\)为0，此时后边的所有\(0\)都变成了\(1\)，那么再加一，会导致一系列的进位，最后让 \(k\) 又变成了1，而其后边的数本身就为0，所以&后结果也为0，只有\(k\)为1。
举个例子：
有一个二进制序列： \(1011000\) 。
取反后得： \(0100111\) 。
加一后得： \(0101000\) 。
前后与得： \(0001000\) 。

建树

我们知道， \(c[i]\) 维护的范围是 \([i-lowbit(i)+1,i]\) 因此我们可以通过前缀和建树。

int t[N];
void init(){
    for(int i=1;i<=n;i++)
        t[i]=sum[i]-sum[i-lowbit(i)];
}

区间查询

如果要查询 \([l,r]\) 我们可以求出前缀和 \([1,r]\) 和 \([1,l-1]\) ，将其相减，就能得到。
所以我们可以将区间问题变为前缀和问题。
即我们需要计算 \([1,x]\) 的和。
我们知道， \(t[i]\) 维护的右端点一定是等于 \(i\) 的，那么在跳到其维护左端点以下的 \(t[i-lowbit(i)]\) 直到跳到头。
其复杂度是 \(O(\log n)\) ，即最需要跳 \(\log n\) 次 \(i\) 。

get_sum(int x){
    int cnt=0;
    while(x){
        cnt+=t[x];
        x-=lowbit(x);
    }
    return cnt;
}

单点修改

修改一个点只需要修改其所有父节点，将本身加上 \(lowbit\) ，得到父节点。
复杂度 \(O(\log n)\)

void add(int x,int k){
    while(x<n)
        t[x]+=k,x+=lowbit(x);
}

区间修改

一个个修就行，复杂度 \(O(n\log n)\) 。