并查集

基本概念

并查集实际上就是处理一个森林问题，每棵树可以看作一个单独的集合，主要作用是根据一些条件进行集合与集合之间的合并以及查询操作，有时也会有删点和转移，但并不常见(本博不讲)。
并查集先是把每个节点（即元素）看作一个单独的集合，接着通过改变每个节点对于父亲节点的映射，做到合并等操作，如下图。

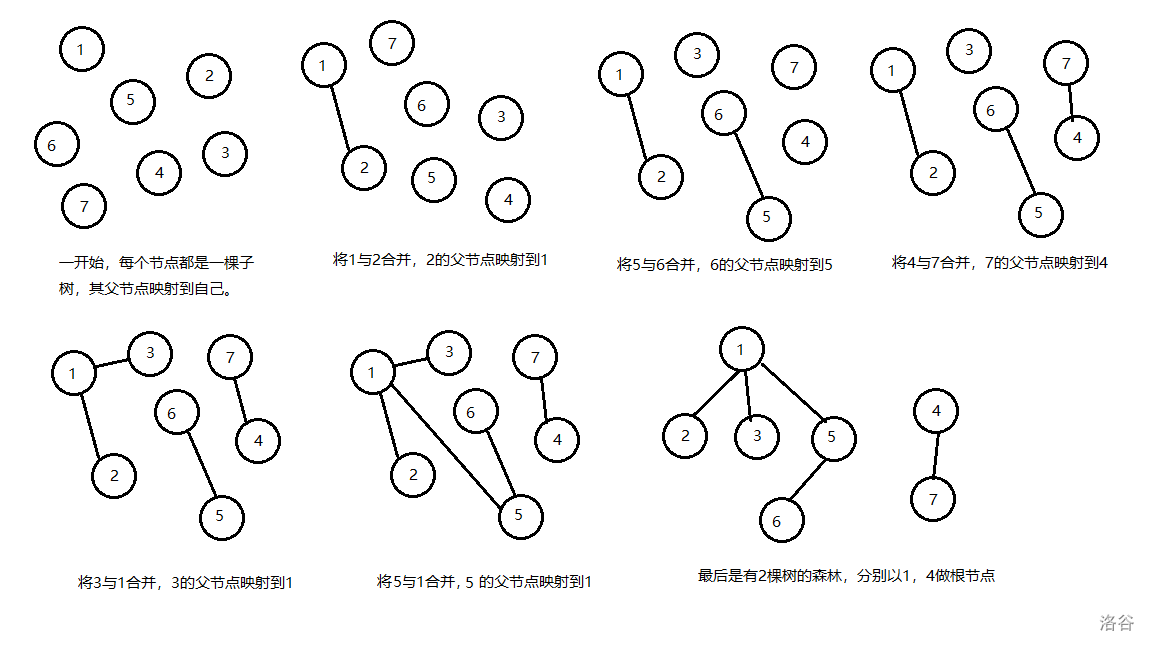
基本代码实现

初始化

我们定义一个f[N]数组，记录每个节点当前的父节点，一开始，他们自己就是一个集合，所以父节点就是自己，同时，所有根的父节点均为自己。

int f[N]
void init(){
    for(int i=1;i<=n;i++)f[i]=i;
}

查询根节点

要查询点x所在的树的根节点，只需要递归即可，向上找。

int find(int x){
    if(f[x]==x)return x;//为根
    find(f[x]);
}

路径压缩

一棵子树中所有节点都归属于根节点这个集合，所以我们可以直接将所有节点的父节点指向根。

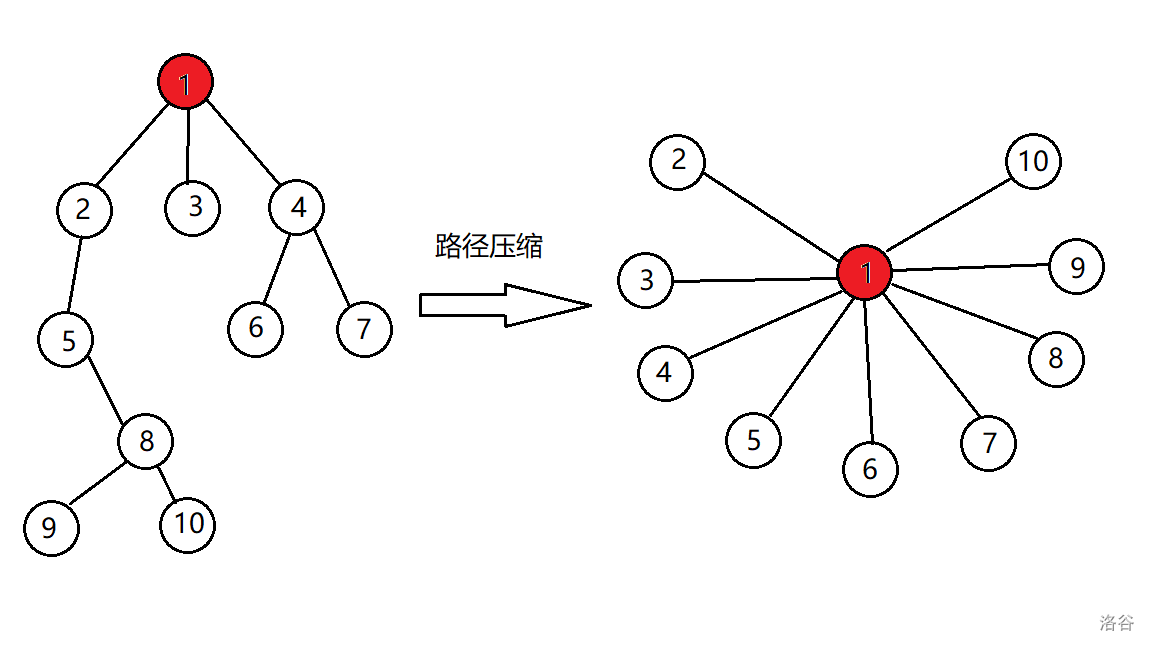
int find(int x){
    if(f[x]!=x)x=find(f[x]);
    return x;
}

合并

将其中一个点的根的父节点映射到另一个点的根。
谁映射谁视情况而定，一般是将节点少的映射到节点多的，即将节点少的插进多的。

f[find(x)]=find(y);

带权并查集

可以将f[N]用结构体多开一个维度，或再开新的数组，带权的权值可能不止一种，在路径压缩与合并时需更新权值。
我们定义数组d[N]记录每个点的权值。

路径压缩

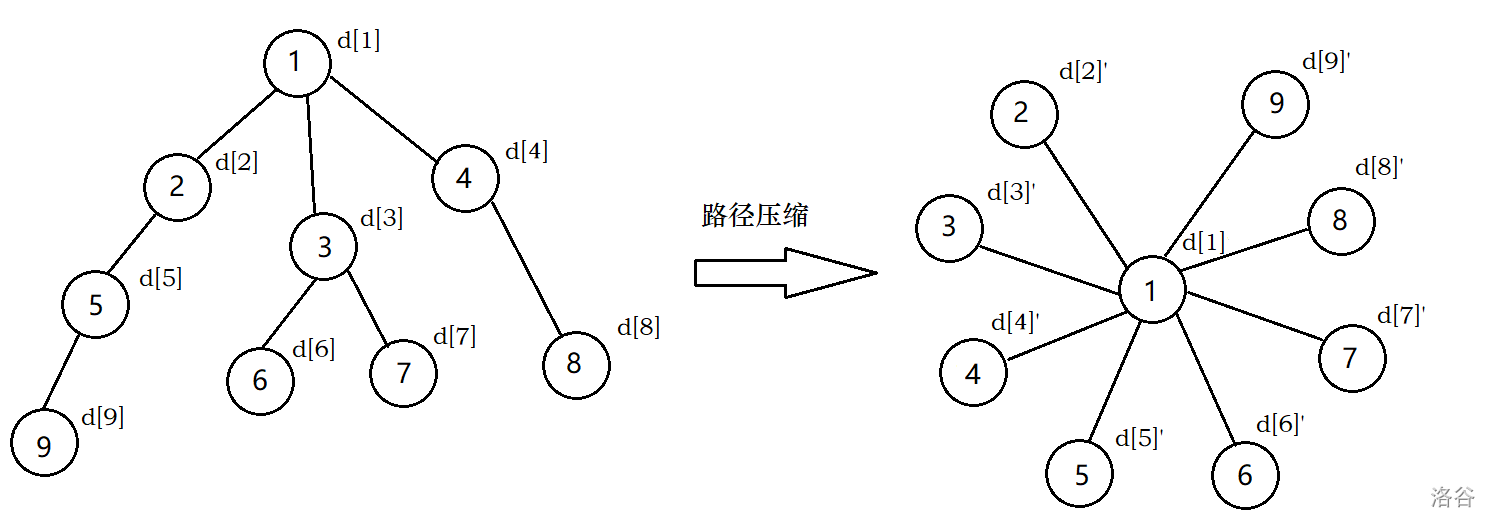
如上图所示，我们将原来的权值\(d[i]\)压缩后改为\(d[i]'\)而转换的规则要看题目，我们这里将\(d[i]\)的权值设为从\(d[i]\)到\(d[1]\)(根)的权值之和。如\(d[7]'=d[7]+d[3]+d[1]\)。
由此我们可以写出以下函数。

int find(int x){
    if(x!=f[x]){
        int fa=f[x];
        f[x]=find(f[x]);//更新父节点
        d[x]+=d[fa];//当前权值是自己加父节点，即递归回溯后统计
    }
    return f[x];
}

当然，题目中的权值和更新规则千奇百怪，要学会随机应变。

合并

将\(x\)映射到\(y\)，即\(y\)的权值增加\(x\)。

启发式合并

按照某一种规律合并，如按权值小的合并到大的，按树的深度合并等等。
我认为属于一种小优化，反正并查集那么快。

习题

P2024
P1196
P1197