线段树

What is「线段树」

线段树是以 \(O(\log n)\) 级别的优秀复杂度维护实现单点修改、区间修改、区间查询，缺点是「我从没有见过有人写线段树能少于50行的」。
码量十分惊人，但大多都是模板所以线段树的学习中，模板是很重要的。

线段树的原理及模板代码

「线段树」之所以叫线段树，是因为他是结合了二叉树的数据结构。

基础索引函数

从根节点依次标号，根为1，一个非叶节点的左右子树就是i*2和i*2+1，由此我们可以写出两个索引函数。

int ans[N];
int ls(int x){return x*2;}//返回左子树
int rs(int x){return x*2+1;}//返回右子树

建树函数

对于一个长度为 \(n\) 的数组 \(a\) ，将区间 \([1,n]\) 当作根节点，取它们的中间值 \(mid\) 将其分为 \([1,mid]\)，\([mid+1,n]\) 两个区间，作为其左右子树，再对每个子树取 \(mid\) 值，再分，直到只有单个元素（叶节点），这样就能得到一个线段树了(如下图)。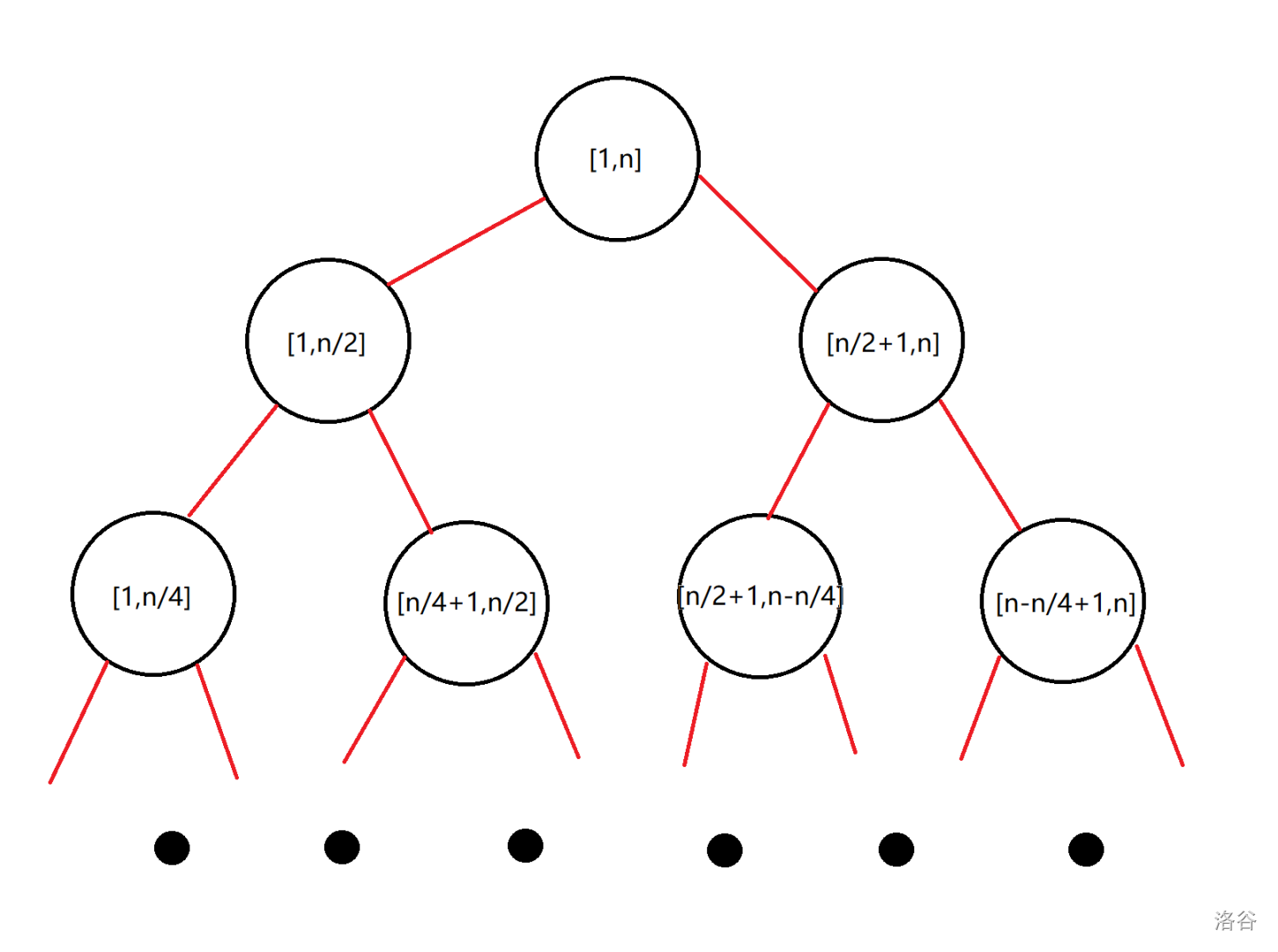
这样我们就实现了建树(类似分治的思想)。

int ans[N],a[N];
void push_up(int x){//这个函数是对于回溯后节点的处理，根据题目需求，维护和，最大值最小值均可，即向上返回值。
    ans[x]=ans[ls(x)]+ ans[rs(x)];
}
int build(int p,int l,int r){//建树函数，p是当前节点,l,r是区间
    if(l==r)return ans[p]=a[p];//如果是叶子节点，才赋值。
    int mid=(l+r)/2;
    build(ls(p),l,mid);
    build(rs(p),mid+1,r);//分治
    pushu_up(p);//维护信息
}

懒标记与区间修改

在此之前，为了减轻代码量，我们将单点修改归为区间长度为1的区间修改。
所谓区间修改就是将整个区间修改，最朴素的做法是枚举所有元素，再一个个返回。
举例，我们要将 \([l,r]\) 的所有值改为 x。

void update(int l,int r,int x){
    for(int i=l;i<=r;i++)a[i]=x;
    build(1,l,r);
}

总复杂度是 \(O(n)\) 遍历整棵树的复杂度为 \(O(n)\) 。
这个复杂度是非常弱的，于是我们就需要用 \(lazetag\) 即「懒标记」，达到 \(O(\log n)\)
所谓懒标记就是通过对节点的延迟标记做到减少搜索次数，只将一个区间节点打懒标记，若不更新其子节点，则保留之前的信息，之后将利用懒标记进行查询，如果发现需修改递归的子节点的父亲有懒标记，则将父节点懒标记归零，分给他的子节点，打懒标记的具体实现流程如下。
我们令 \([nl,nr]\) 为需要修改的区间，tag[N]为懒标记。

1. • 从根节点开始递归，往下搜索子树。
2. • 如果该节点被区间完全包含，即if(nl<=l&&r<=nr)，那么给该节点的编号打上懒标记，即处理tag[p]，并修改当前节点的值，结束修改。
3. • 如果该节点并没有被完全包含，清空当前懒标记，将懒标记递归给左右子树，继续执行2。

int f(int l,int r,int p,int x){//更新懒标记
    tag[p]=x;//将懒标记改为x
    ans[p]=x*(r-l+1);//更新当前节点的值
}
int push_down(int l,int r,int p){//将该节点的懒标记传给子节点
    int mid=(l+r)/2;
    f(l,mid,ls(p),tag[p]);
    f(mid+1,r,rs(p),tag[p]);//更新子节点
    tag[p]=0;
}
void update(int nl,int nr,int l,int r,int p,int k){
    if(nl<=l&&r<=nr){
        f(l,r,p,x);
        return 0；
    }
    push_down(l,r,p);//更新懒标记
    int mid=(l+r)/2;
    if(nl<=mid)update(nl,nr,l,mid,ls(p),k);
    if(nr>mid) update(nl,nr,mid+1,r,rs(p),k);//递归左右子树
    push_up(p);//回溯更新该节点
}

区间查询

这个操作与区间修改类似，一样判断是否包含，一样更新懒标记，一样递归，只不过把改值变为统计。

int query(int qx,int qy,int l,int r,int p){//区间查询 
    int res=0;//统计
    if(qx<=l&&r<=qy)return ans[p];//如果完全包含，返回该节点值
    int mid=(l+r)/2;
    push_down(p,l,r);//更新懒标记
    if(qx<=mid)res+=query(qx,qy,l,mid,ls(p));
    if(qy>mid) res+=query(qx,qy,mid+1,r,rs(p));//往下递归子树
    return res;
}

完整代码

#include<bits/stdc++.h>
const int N=1e5+5;
using namespace std;
int n,m,a[N],ans[N<<2],tag[N<<2];
int ls(int x){ 
    return x*2;
}
int rs(int x){
    return x*2+1;
}
void push_up(int p){
    ans[p]=ans[ls(p)]+ans[rs(p)];
}
void build(int p,int l,int r){
    tag[p]=0;
    if(l==r){
		ans[p]=a[l];
		return;
	}
    int mid=(l+r)/2;
    build(ls(p),l,mid);
    build(rs(p),mid+1,r);
    push_up(p);
}
void f(int p,int l,int r,int k){
    tag[p]+=k;
    ans[p]+=k*(r-l+1);
}
void push_down(int p,int l,int r){
    int mid=(l+r)/2;
    f(ls(p),l,mid,tag[p]);
    f(rs(p),mid+1,r,tag[p]);
    tag[p]=0;
}
void update(int nl,int nr,int l,int r,int p,int k){
    if(nl<=l&&r<=nr){
    	f(p,l,r,k);
        return;
    }
    push_down(p,l,r);
    int mid=(l+r)/2;
    if(nl<=mid)update(nl,nr,l,mid,ls(p),k);
    if(nr>mid) update(nl,nr,mid+1,r,rs(p),k);
    push_up(p);
}
int query(int qx,int qy,int l,int r,int p){
    int res=0;
    if(qx<=l&&r<=qy)return ans[p];
    int mid=(l+r)/2;
    push_down(p,l,r);
    if(qx<=mid)res+=query(qx,qy,l,mid,ls(p));
    if(qy>mid) res+=query(qx,qy,mid+1,r,rs(p));
    return res;
}

习题

P3372
P3373
P1253
P1276
P1471