背包问题
01背包是在M件物品取出若干件放在空间为W的背包里，每件物品的重量为W1，W2至Wn，与之相对应的价值为V1V2至Vn。01背包是背包问题中最简单的问题。01背包的约束条件是给定几种物品，每种物品有且只有一个(这个与完全背包不同)，并且有价值和重量两个属性。在01背包问题中，因为每种物品只有一个，对于每个物品只需要考虑选与不选两种情况。如果不选择将其放入背包中，则不需要处理。如果选择将其放入背包中，由于不清楚之前放入的物品占据了多大的空间，需要枚举将这个物品放入背包后可能占据背包空间的所有情况。
1. 解析
在解决问题之前，为描述方便，首先定义一些变量：Vi表示第 i 个物品的价值，Wi表示第 i 个物品的体积，定义V(i,j)：当前背包容量 j，前 i 个物品最佳组合对应的价值，同时背包问题抽象化（X1，X2，…，Xn，其中 Xi 取0或1，表示第 i 个物品选或不选）。
1、建立模型，即求max(V1X1+V2X2+…+VnXn)；
2、寻找约束条件，W1X1+W2X2+…+WnXn<capacity；
3、寻找递推关系式，面对当前商品有两种可能性：
包的容量比该商品体积小，装不下，此时的价值与前i-1个的价值是一样的，即V(i,j)=V(i-1,j)；
还有足够的容量可以装该商品，但装了也不一定达到当前最优价值，所以在装与不装之间选择最优的一个，即V(i,j)=max｛V(i-1,j)，V(i-1,j-w(i))+v(i)｝。
其中V(i-1,j)表示不装，V(i-1,j-w(i))+v(i) 表示装了第i个商品，背包容量减少w(i)，但价值增加了v(i)；
由此可以得出递推关系式：
j<w(i) V(i,j)=V(i-1,j)
j>=w(i) V(i,j)=max｛V(i-1,j)，V(i-1,j-w(i))+v(i)｝
这里需要解释一下，为什么能装的情况下，需要这样求解（这才是本问题的关键所在！）：
可以这么理解，如果要到达V(i,j)这一个状态有几种方式？
肯定是两种，第一种是第i件商品没有装进去，第二种是第i件商品装进去了。没有装进去很好理解，就是V(i-1,j)；装进去了怎么理解呢？如果装进去第i件商品，那么装入之前是什么状态，肯定是V(i-1,j-w(i))。由于最优性原理（上文讲到），V(i-1,j-w(i))就是前面决策造成的一种状态，后面的决策就要构成最优策略。两种情况进行比较，得出最优。
4、填表，首先初始化边界条件，V(0,j)=V(i,0)=0；
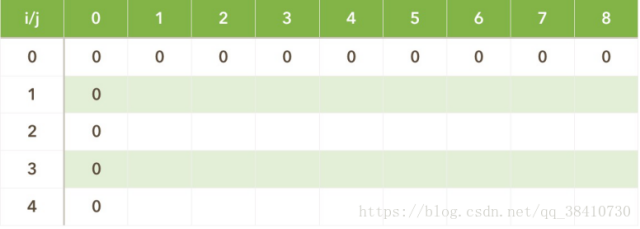
然后一行一行的填表：
如，i=1，j=1，w(1)=2，v(1)=3，有j<w(1)，故V(1,1)=V(1-1,1)=0；
又如i=1，j=2，w(1)=2，v(1)=3，有j=w(1),故V(1,2)=max｛ V(1-1,2)，V(1-1,2-w(1))+v(1) ｝=max｛0，0+3｝=3；
如此下去，填到最后一个，i=4，j=8，w(4)=5，v(4)=6，有j>w(4)，故V(4,8)=max｛ V(4-1,8)，V(4-1,8-w(4))+v(4) ｝=max｛9，4+6｝=10……
所以填完表如下图：
5、表格填完，最优解即是V(number,capacity)=V(4,8)=10。
2. 设计
当 j >= wi 时, m(i, j) = max { m(i-1, j), m(i-1, j-wi) + vi };
当 j < wi 时， m(i, j) = m(i-1, j)
3. 分析
时间复杂度为O(n)
4. 源码
#include<iostream>
using namespace std;
#include <algorithm>
int w[5] = { 0 , 2 , 3 , 4 , 5 };
int v[5] = { 0 , 3 , 4 , 5 , 6 };
int bagV = 8;
int dp[5][9] = { { 0 } };
int item[5];
void findMax() {
for (int i = 1; i <= 4; i++) {
for (int j = 1; j <= bagV; j++) {
if (j < w[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
}
void findWhat(int i, int j) {
if (i >= 0) {
if (dp[i][j] == dp[i - 1][j]) {
item[i] = 0;
findWhat(i - 1, j);
}
else if (j - w[i] >= 0 && dp[i][j] == dp[i - 1][j - w[i]] + v[i]) {
item[i] = 1;
findWhat(i - 1, j - w[i]);
}
}
}
void print() {
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 9; j++) {
cout << dp[i][j] << ' ';
}
cout << endl;
}
cout << endl;
for (int i = 0; i < 5; i++)
cout << item[i] << ' ';
cout << endl;
}
int main()
{
findMax();
findWhat(4, 8);
print();
return 0;
}
