ntt番外篇
多项式求逆
传送门
对于次数小于n-1的多项式F(x),求其对于\(x^n\)的逆,系数对998244353取模。保证有解
一个简单的递推思想。
设逆为\(G(x)\),\(F(x)\)在\(mod\qquad x^m\)下的一个逆为\(H(x)\)。
则有\(F(x)(G(x)-H(x))=0 \quad(mod \quad x^m)\),
因为逆存在,\(F(x)\)存在常数项,故可将\(F(x)\)约去,得
\(G(x)-H(x)=0 \quad(mod \quad x^m)\),平方后得
\(G(x)^2-2G(x)H(x)+H(x)^2=0 \quad(mod \quad x^{2m})\)(注意不能先将H(x)移项再平方,否则模数不能平方),两边同乘\(F(x)\)并移项,
\(G(x)=2H(x)-F(x)G(x)^2 \quad(mod \quad x^{2m})\)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
const ll mod=998244353;
const int maxn=4e6;
template<typename T>
inline void read(T &x){
x=0;T fl=1;char tmp=getchar();
while(tmp<'0'||tmp>'9')fl=tmp=='-'?-fl:fl,tmp=getchar();
while(tmp>='0'&&tmp<='9')x=(x<<1)+(x<<3)+tmp-'0',tmp=getchar();
x=x*fl;
}
inline ll pw(ll x,ll n,ll p){
ll ans=1;
while(n){
if(n&1)ans=ans*x%p;
x=x*x%p,n>>=1;
}
return ans;
}
inline ll root(const ll p){
ll pri[60],cnt=0;
ll x=p-1;
for(int k=2;k*k<=p-1;k++){
if(x%k==0){
pri[++cnt]=k;
while(x%k==0)x/=k;
}
}
if(x>1)pri[++cnt]=x;
int fl;
for(int i=2;i<=p;i++){
fl=0;
for(int j=1;j<=cnt;j++){
if(pw(i,(p-1)/pri[j],p)==1){
fl=1;
break;
}
}
if(!fl)return i;
}
throw;
}
inline void exgcd(const ll a,const ll b,ll &x, ll &y){
if(!b)x=1,y=0;
else exgcd(b,a%b,y,x),y+=mod-a/b*x%mod;
}
inline ll inv(const ll a,const ll p){//must exist
ll x,y;
exgcd(a,p,x,y);
return x%p;
}
struct NumberTheoreticTransform{
ll omega[maxn],iomega[maxn];
void init(const int n,const ll p){
ll g=root(p),x=pw(g,(p-1)/n,p),ix=inv(x,p);
omega[0]=iomega[0]=1;
for(int i=1;i<n;i++){
omega[i]=omega[i-1]*x%p;
iomega[i]=iomega[i-1]*ix%p;
}
}
void transform(ll *a,const int n,ll *omega){
int k=0;
while((1<<k)<n)k++;
for(int i=0;i<n;i++){
int t=0;
for(int j=0;j<k;j++) if(i&(1<<j))t|=1<<k-j-1;
if(t>i)swap(a[i],a[t]);
}
for(int l=2;l<=n;l<<=1){
int m=l/2,d=n/l;
for(ll *p=a;p!=a+n;p+=l){
for(int i=0;i<m;i++){
int t=omega[d*i]*p[i+m]%mod;
p[i+m]=p[i]-t+mod;
p[i]=p[i]+t;
}
}
}
for(int i=0;i<n;i++)
a[i]=a[i]%mod;
}
void dft(ll *a,const int n){
transform(a,n,omega);
}
void idft(ll *a,const int n){
transform(a,n,iomega);
ll x=inv(n,mod);
for(int i=0;i<n;i++)
a[i]=a[i]*x%mod;
}
}ntt;
inline int solve(const ll *a1,const int n1,const ll *a2,const int n2,ll *w){
int n=1;
while(n<n1+n2)n<<=1;
static ll c1[maxn],c2[maxn];
for(int i=0;i<n;i++)c1[i]=c2[i]=0;
for(int i=0;i<n1;i++)c1[i]=a1[i];
for(int i=0;i<n2;i++)c2[i]=a2[i];
ntt.init(n,mod);
ntt.dft(c1,n),ntt.dft(c2,n);
for(int i=0;i<n;i++)c1[i]=c1[i]*c2[i]%mod;
ntt.idft(c1,n);
for(int i=0;i<n;i++)w[i]=c1[i];
return n1+n2-1;
}
ll a[maxn],b[maxn],c[maxn];
int n;
signed main(){
cin>>n;
for(int i=0;i<n;i++)
read(a[i]);
b[0]=c[0]=inv(a[0],mod);
int m=1;
while(m<n)m<<=1;
for(int l=2;l<=m;l<<=1){
solve(a,l,b,l,c);
solve(c,l,b,l,c);
for(int i=0;i<l;i++){
c[i]=((-c[i]+2*b[i])%mod+mod)%mod;
b[i]=c[i];
}
}
for(int i=0;i<n;i++)
printf("%lld ",c[i]);
puts("");
return 0;
}
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
const ll mod=998244353;
const int maxn=4e6;
template<typename T>
inline void read(T &x){
x=0;T fl=1;char tmp=getchar();
while(tmp<'0'||tmp>'9')fl=tmp=='-'?-fl:fl,tmp=getchar();
while(tmp>='0'&&tmp<='9')x=(x<<1)+(x<<3)+tmp-'0',tmp=getchar();
x=x*fl;
}
inline ll pw(ll x,ll n,ll p){
ll ans=1;
while(n){
if(n&1)ans=ans*x%p;
x=x*x%p,n>>=1;
}
return ans;
}
inline ll root(const ll p){
ll pri[60],cnt=0;
ll x=p-1;
for(int k=2;k*k<=p-1;k++){
if(x%k==0){
pri[++cnt]=k;
while(x%k==0)x/=k;
}
}
if(x>1)pri[++cnt]=x;
int fl;
for(int i=2;i<=p;i++){
fl=0;
for(int j=1;j<=cnt;j++){
if(pw(i,(p-1)/pri[j],p)==1){
fl=1;
break;
}
}
if(!fl)return i;
}
throw;
}
inline void exgcd(const ll a,const ll b,ll &x, ll &y){
if(!b)x=1,y=0;
else exgcd(b,a%b,y,x),y+=mod-a/b*x%mod;
}
inline ll inv(const ll a,const ll p){//must exist
ll x,y;
exgcd(a,p,x,y);
return x%p;
}
struct NumberTheoreticTransform{
ll omega[maxn],iomega[maxn];
void init(const int n,const ll p){
ll g=root(p),x=pw(g,(p-1)/n,p),ix=inv(x,p);
omega[0]=iomega[0]=1;
for(int i=1;i<n;i++){
omega[i]=omega[i-1]*x%p;
iomega[i]=iomega[i-1]*ix%p;
}
}
void transform(ll *a,const int n,ll *omega){
int k=0;
while((1<<k)<n)k++;
for(int i=0;i<n;i++){
int t=0;
for(int j=0;j<k;j++) if(i&(1<<j))t|=1<<k-j-1;
if(t>i)swap(a[i],a[t]);
}
for(int l=2;l<=n;l<<=1){
int m=l/2,d=n/l;
for(ll *p=a;p!=a+n;p+=l){
for(int i=0;i<m;i++){
int t=omega[d*i]*p[i+m]%mod;
p[i+m]=p[i]-t+mod;
p[i]=p[i]+t;
}
}
}
for(int i=0;i<n;i++)
a[i]=a[i]%mod;
}
void dft(ll *a,const int n){
transform(a,n,omega);
}
void idft(ll *a,const int n){
transform(a,n,iomega);
ll x=inv(n,mod);
for(int i=0;i<n;i++)
a[i]=a[i]*x%mod;
}
}ntt;
inline int solve(const ll *a1,const int n1,const ll *a2,const int n2,ll *w){
int n=1;
while(n<n1+n2)n<<=1;
static ll c1[maxn],c2[maxn];
for(int i=0;i<n;i++)c1[i]=c2[i]=0;
for(int i=0;i<n1;i++)c1[i]=a1[i];
for(int i=0;i<n2;i++)c2[i]=a2[i];
ntt.init(n,mod);
ntt.dft(c1,n),ntt.dft(c2,n);
for(int i=0;i<n;i++)c1[i]=c1[i]*c2[i]%mod;
ntt.idft(c1,n);
for(int i=0;i<n;i++)w[i]=c1[i];
return n1+n2-1;
}
ll f[maxn],g[maxn];
ll ig[maxn],tmp[maxn];
ll q[maxn],r[maxn];
int n,m;
signed main(){
cin>>n>>m;n++,m++;
int lq=n-m+1,lr=m-1;
for(int i=n-1;i>=0;i--)
read(f[i]);
for(int i=m-1;i>=0;i--)
read(g[i]);
tmp[0]=ig[0]=inv(g[0],mod);
int len=1;
while(len<lq)len<<=1;
for(int l=2;l<=len;l<<=1){
solve(tmp,l/2,tmp,l/2,ig);
solve(ig,l,g,l,ig);
for(int i=0;i<l;i++){
ig[i]=(-ig[i]+2*tmp[i]+mod)%mod;
tmp[i]=ig[i];
}
}
solve(f,lq,ig,lq,q);
for(int i=0;i<n;i++)
if(i<n-i-1)swap(f[i],f[n-i-1]);
for(int i=0;i<m;i++)
if(i<m-i-1)swap(g[i],g[m-i-1]);
for(int i=0;i<lq;i++)
if(i<lq-i-1)swap(q[i],q[lq-i-1]);
for(int i=0;i<lq;i++)
printf("%lld ",q[i]);
puts("");
solve(q,lq,g,m,r);
for(int i=0;i<lr;i++)
r[i]=(f[i]-r[i]+mod)%mod;
for(int i=0;i<lr;i++)
printf("%lld ",r[i]);
puts("");
return 0;
}
分治fft
题目传送门
这题也可以通过多项式求逆来完成,甚至复杂度更优,也需要推导式子。但暂不是重点。
分治fft的思想在于用fft/ntt维护某些式子的cdq分治。
每次考虑用f[l->mid]辅助得出f[mid+1->r]
\(设val[i]=\sum^{mid}_{j=l}f[j]g[i-j]\)
则val[mid+1->r]可以由f[l->mid]和g[0,r-l]通过一次多项式乘法得到。
每个f[i]至多由\(O(log{n})\)个val[i]得出。
每层二分的复杂度为\(O(nlogn)\)
由此复杂度为\(O(nlog^2n)\)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
template<typename T>
inline void read(T &x){
x=0;T fl=1;char tmp=getchar();
while(tmp<'0'||tmp>'9')fl=tmp=='-'?-fl:fl,tmp=getchar();
while(tmp>='0'&&tmp<='9')x=(x<<1)+(x<<3)+tmp-'0',tmp=getchar();
x=x*fl;
}
typedef unsigned long long ll;
const double Pi=acos(-1);
const int maxn=4.2e5;
const int mod=998244353;
inline ll pw(ll x,ll n,ll p){
ll ans=1;
while(n){
if(n&1)ans=ans*x%p;
x=x*x%p,n>>=1;
}
return ans;
}
inline ll root(const ll p){
ll pri[60],cnt=0;
ll x=p-1;
for(int k=2;k*k<=p-1;k++){
if(x%k==0){
pri[++cnt]=k;
while(x%k==0)x/=k;
}
}
if(x>1)pri[++cnt]=x;
int fl;
for(int i=2;i<=p;i++){
fl=0;
for(int j=1;j<=cnt;j++){
if(pw(i,(p-1)/pri[j],p)==1){
fl=1;
break;
}
}
if(!fl)return i;
}
throw;
}
inline void exgcd(const ll a,const ll b,ll &x, ll &y){
if(!b)x=1,y=0;
else exgcd(b,a%b,y,x),y+=mod-a/b*x%mod;
}
inline ll inv(const ll a,const ll p){//must exist
ll x,y;
exgcd(a,p,x,y);
return x%p;
}
struct NumberTheoreticTransform{
ll omega[maxn],iomega[maxn];
void init(const int n){
ll g=3,x=pw(g,(mod-1)/n,mod),ix=inv(x,mod);
omega[0]=iomega[0]=1;
for(int i=1;i<n;i++){
omega[i]=omega[i-1]*x%mod;
iomega[i]=iomega[i-1]*ix%mod;
}
}
void transform(ll *a,const int n,ll *omega){
int k=0;
while((1<<k)<n)k++;
for(int i=0;i<n;i++){
int t=0;
for(int j=0;j<k;j++)if(i&(1<<j))t|=1<<k-j-1;
if(t>i)swap(a[i],a[t]);
}
for(int l=2;l<=n;l<<=1){
int m=l/2;
for(ll *p=a;p!=a+n;p+=l)
for(int i=0;i<m;i++){
ll t=p[i+m]%mod*omega[n/l*i]%mod;
p[i+m]=p[i]-t+mod;
p[i]=p[i]+t;
}
}
for(int i=0;i<n;i++)
a[i]=a[i]%mod;
}
void dft(ll *a,const int n){
transform(a,n,omega);
}
void idft(ll *a,const int n){
transform(a,n,iomega);
ll x=inv(n,mod);
for(int i=0;i<n;i++)
a[i]=a[i]*x%mod;
}
}ntt;
inline int mlpy(ll *a1,int n1,ll *a2,int n2,ll *w){
int n=1;
while(n<n1+n2)n<<=1;
static ll c1[maxn],c2[maxn];
for(int i=0;i<n;i++)c1[i]=c2[i]=0;
for(int i=0;i<n1;i++)c1[i]=a1[i];
for(int i=0;i<n2;i++)c2[i]=a2[i];
ntt.init(n);
ntt.dft(c1,n),ntt.dft(c2,n);
for(int i=0;i<n;i++)c1[i]=c1[i]*c2[i]%mod;
ntt.idft(c1,n);
n=n1+n2-1;
for(int i=0;i<n;i++)
w[i]=c1[i];
return n;
}
int n,m;
ll g[maxn],f[maxn],v[maxn];
void solve(int l,int r){
if(l==r)return ;
int mid=l+r>>1;
solve(l,mid);
mlpy(f+l,mid-l+1,g,r-l+1,v);
for(int i=mid+1;i<=r;i++)f[i]=(f[i]+v[i-l])%mod;
solve(mid+1,r);
}
signed main(){
// freopen("P4721_6.in","r",stdin);
cin>>n;
for(int i=1;i<n;i++)
read(g[i]);
f[0]=1;
solve(0,n-1);
for(int i=0;i<n;i++)
printf("%lld ",f[i]);
return 0;
}
具体的例子
HDU7162
写出求期望的方程,发现类似卷积。
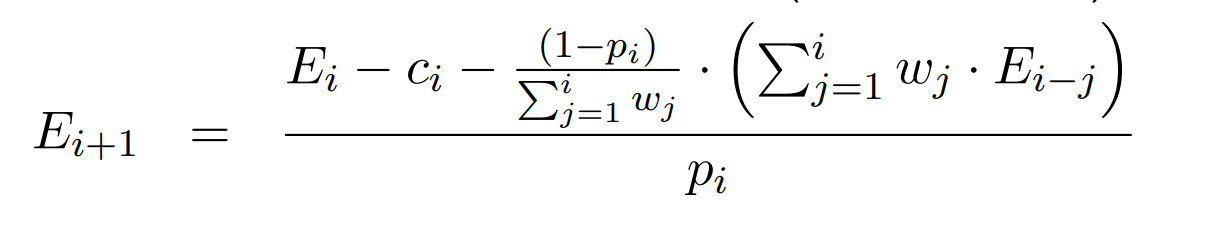
若知道\(E_0\)则可以顺推出\(E_i\)直至\(E_n\),但实际上是已知\(E_n=0\)求\(E_0\)。
由线性关系得\(E_i=a_i*E_0+b_i\)存在唯一\(a_i,b_i\)
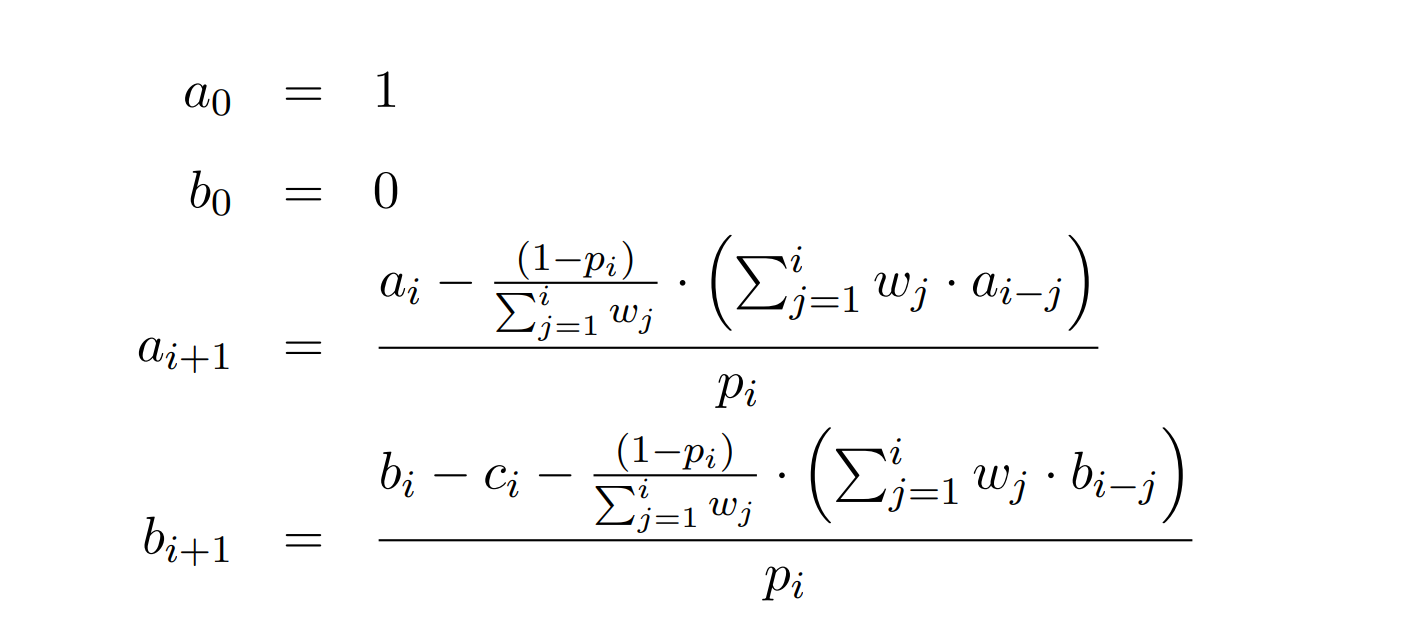
\(a_i,b_i\)可以通过分治ntt求出。\(E_0=-b_n*inv(a_n)\)
时间复杂度仍是\(O(nlog^2n\),注意常数优化。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
template<typename T>
inline void read(T &x){
x=0;T fl=1;char tmp=getchar();
while(tmp<'0'||tmp>'9')fl=tmp=='-'?-fl:fl,tmp=getchar();
while(tmp>='0'&&tmp<='9')x=(x<<1)+(x<<3)+tmp-'0',tmp=getchar();
x=x*fl;
}
const int maxn=2.2e5;
const ll mod=998244353;
inline ll pw(ll x,int n){
ll ans=1;
while(n){
if(n&1)ans=ans*x%mod;
x=x*x%mod,n>>=1;
}
return ans;
}
inline ll inv(const ll x){
return pw(x,mod-2);
}
struct NumberTheoreticTransform{
ll omega[maxn],iomega[maxn];
void init(const int n){
ll g=3,x=pw(g,(mod-1)/n),ix=inv(x);
omega[0]=iomega[0]=1;
for(int i=1;i<n;i++){
omega[i]=omega[i-1]*x%mod;
iomega[i]=iomega[i-1]*ix%mod;
}
}
void transform(ll *a,const int n,ll *omega){
int k=0;
while((1<<k)<n)k++;
for(int i=0;i<n;i++){
int t=0;
for(int j=0;j<k;j++)if(i&(1<<j))t|=1<<k-j-1;
if(t<i)swap(a[t],a[i]);
}
for(int l=2;l<=n;l<<=1){
int m=l/2;
for(ll *p=a;p!=a+n;p+=l)
for(int i=0;i<m;i++){
ll t=p[i+m]*omega[n/l*i]%mod;
p[i+m]=(p[i]+mod-t)%mod;
p[i]=(p[i]+t)%mod;
}
}
}
void dft(ll *a,const int n){
transform(a,n,omega);
}
void idft(ll *a,const int n){
transform(a,n,iomega);
ll x=inv(n);
for(int i=0;i<n;i++)
a[i]=a[i]*x%mod;
}
}ntt;
inline int mlpy(const ll *a1,const int n1,const ll *a2,const int n2,ll *w){
int n=1;
while(n<n2)n<<=1;
static ll c1[maxn],c2[maxn];
fill(c1,c1+n,0),fill(c2,c2+n,0);
for(int i=0;i<n1;i++)c1[i]=a1[i];
for(int i=0;i<n2;i++)c2[i]=a2[i];
ntt.init(n);
ntt.dft(c1,n),ntt.dft(c2,n);
for(int i=0;i<n;i++)c1[i]=c1[i]*c2[i]%mod;
ntt.idft(c1,n);
for(int i=0;i<n;i++) w[i]=c1[i];
return n1+n2-1;
}
int n;
ll w[maxn],p[maxn],c[maxn];
ll sw[maxn];
ll a[maxn],b[maxn],v[maxn];
ll fa[maxn],fb[maxn];
void solve(int l,int r){
if(l==r){
a[l+1]=(a[l]-(1-p[l])*inv(sw[l])%mod*fa[l]%mod+mod)*inv(p[l])%mod;
b[l+1]=(b[l]-c[l]-(1-p[l])*inv(sw[l])%mod*fb[l]%mod+mod*2)*inv(p[l])%mod;
return ;
}
int mid=l+r>>1;
solve(l,mid);
mlpy(a+l,mid-l+1,w,r-l+1,v);
for(int i=mid+1;i<=r;i++)
fa[i]=(fa[i]+v[i-l])%mod;
mlpy(b+l,mid-l+1,w,r-l+1,v);
for(int i=mid+1;i<=r;i++)
fb[i]=(fb[i]+v[i-l])%mod;
solve(mid+1,r);
}
signed main(){
// freopen("1001.in","r",stdin);
// freopen("01.out","w",stdout);
int T;cin>>T;
while(T--){
cin>>n;
for(int i=0;i<n;i++)
read(p[i]),read(c[i]);
for(int i=1;i<n;i++)
read(w[i]);
sw[0]=0;
for(int i=1;i<n;i++)
sw[i]=sw[i-1]+w[i];
for(int i=0;i<n;i++)
p[i]=p[i]*inv(100)%mod;
fill(fa,fa+n+1,0);
fill(fb,fb+n+1,0);
a[0]=1,b[0]=0;
solve(0,n-1);
printf("%lld\n",(mod-b[n])*inv(a[n])%mod);
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号