分治法简单应用

大整数乘法分治

缅怀Gauss
欲求\(X*Y=?\)，令\(X,Y均为n位，X=A*10^{n/2}+B,Y=C*10^{n/2}+D\)
\(XY=AC*10^{n}+BD+(AD+BC)*10^{n/2}\) →复杂度\(O(n^2)\)
\(XY=AC*10^{n}+BD+((A-B)(D-C)+AC+BD)*10^{n/2}\)
\(XY=AC*10^{n}+BD+((A+B)(C+D)-AC-BD)*10^{n/2}\)
改进后六次加法+3次乘法,\(T(n)=3T(n/2)+O(n)→T(n)=O(n^{lg3})=O(n^1.59)\)
再优化后就是fft和ntt

strassen矩阵乘法

假设n为2的指数（不足则将矩阵添零补到n阶矩阵）


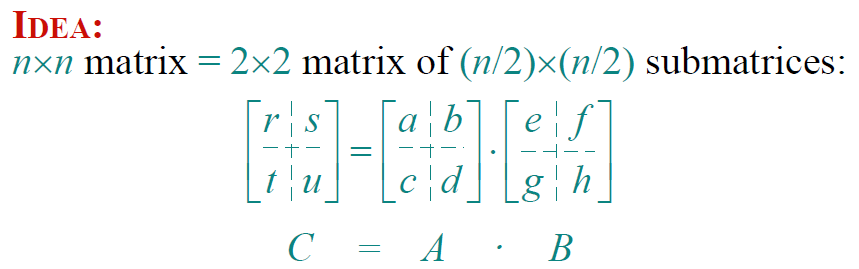
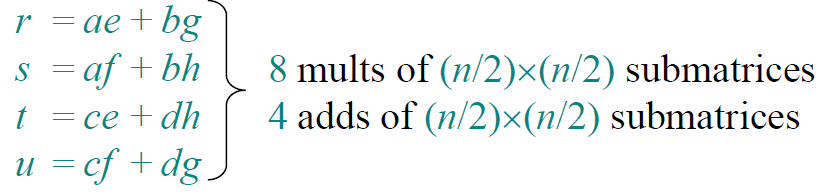
用上述大整数乘法类似的处理方法，P负责乘法，可证明这种方式至少需要7次乘法

\(T(n)=7T(n/2)+O(n)→T(n)=O(n^{log7})=O(n^{2.81})\)

快排和归并性能分析

实践证明当对数组进行排序的时候，快速排序的速度优于归并排序。对于链表，是归并排序的速度优于快速排序。
一般数组中，快排在排序的过程中是访问连续的一个列表；而归并（两个归到一个）是在不停的访问两个列表。
但，当快排访问的不是连续的列表时，而是访问列表等时，就和归并相比就没有优势了。

二维最近点对

取点对在x上中位数，求出左右n/2个点对的最小距离d1,d2，令d=min(d1,d2).
考虑将两个子问题合并，需要求出所有经过分割线的点对的最小距离。
可知对于左区间的某点p，右侧存在的距离小于d的点q必然在一个d*2d的区域α中。
α各点间距离大于等于d，至多有六个点在α内。
故合并花费为O(n)+O(nlogn)[排序花费]
如果把整个过程嵌入归并排序，则可以省去一个log。这也是分治的一个常用技巧
最终结果\(O(nlog^2n)\)

循环赛制表

分治法

当n为偶数时，直接合并n/2的子表；当n为奇数时，因为比赛天数不变，先令求n+1时的表，再将和n+1比赛的选手轮空。
注意保留表头，使得所有人都和1~n（包括自己）“比赛”过，方便合并。
再考虑合并的问题：
1将两个偶数子表合并，就是先复制再互换。
2将奇数子表合并时，会要求轮空的选手必须匹配到对手。还是先复制到右侧，然后两个轮空的选手加赛。剩下n/2-1场比赛，直接构造：会发现加赛的选手刚好形成一个排列，将排列不断左移，并在右侧补上对应的选手即可。

123456
210540
301604
032065

123456
216543
351624
432165

123456
216543
351624
432165
564
645

123456
216543
351624
432165
564312
645231

非分治法

another