jzoj4196 二分图计数 解题报告(容斥原理)

Description

 

Input

Output

 

Sample Input

样例1
1 2
0

样例2
3 3
0
1
2

Sample Output

样例1
1

样例2
70

 

Data Constraint

 

考试的时候，我这样的蒟蒻当然是写不出来的，直到看了其他大佬的题解我才A掉。我不会告诉你们我提交的次数差不多20次，各种心态爆炸漏掉文件输入输出什么的

考完试之后听到别人说这题是容斥，我就自己想了一下，发现搞不定啊。2ⁿ枚举S，再来2ⁿ枚举S1，这时间不对劲啊。没想到竟然直接是3ⁿ枚举

下面是题解：

这个容斥的意思就是当S1是空集的时候，S-S1=S可以任意匹配；但是这样就一定会让某个点x和不能与自己匹配的点去匹配，然后就需要减去。然而若是存在两点x,y，一次x在S1、y在S-S1中，一次y在S1、x在S-S1中，它们都与跟自己不连边的点匹配的情况会被减两次，于是又要加回来…… 

这题还有个地方很难办，就是在容斥的时候我们不能把右边集合的点重复匹配，即我们的生成集合S1不能随意生成。解决这个问题的方法就是把数组a离散化(a[i]表示左边的点i不与右边某个点匹配)，

然后我们在生成S1的时候状态压缩一下，判断当前的不匹配点是否已经被匹配了(注意我们容斥的对象，黑体部分的匹配的含义有区别，前者是输入的不匹配)。

那么怎么在生成子集的同时我们怎么计算F(S)呢？考虑预处理出s[i][j]数组，表示当l1=i、l2=j时，H(S,S1)的值(l1=|S1|,l2=|S-S1|)。这样我们就可以在O(1)的时间复杂度内调用。

预处理的方法就是

for (int i=0;i<=n;i++)
    {
        s[i][0]=1;int tmp=m-i;
        for (int j=1;j<=n;j++) s[i][j]=1ll*s[i][j-1]*tmp--%mod;
    }

即我们已经确定右边m-i个点被匹配，求剩下的匹配方案数。正如题解说的，“任意匹配又不需要在乎所连的边"轻松O(n²)搞定

于是总的时间复杂度就是O(n²(预处理)+3ⁿ(计算F(S))+2ⁿ(统计答案)

还有值得注意的是在dfs里我们判断现在容斥是加还是减是通过l1的奇偶性判断，而如果是奇数的话就是减，减得话。。。就改成减(mod-1)*s[l1][l2]再去模，如果不是这样的话下场就会是这样的：

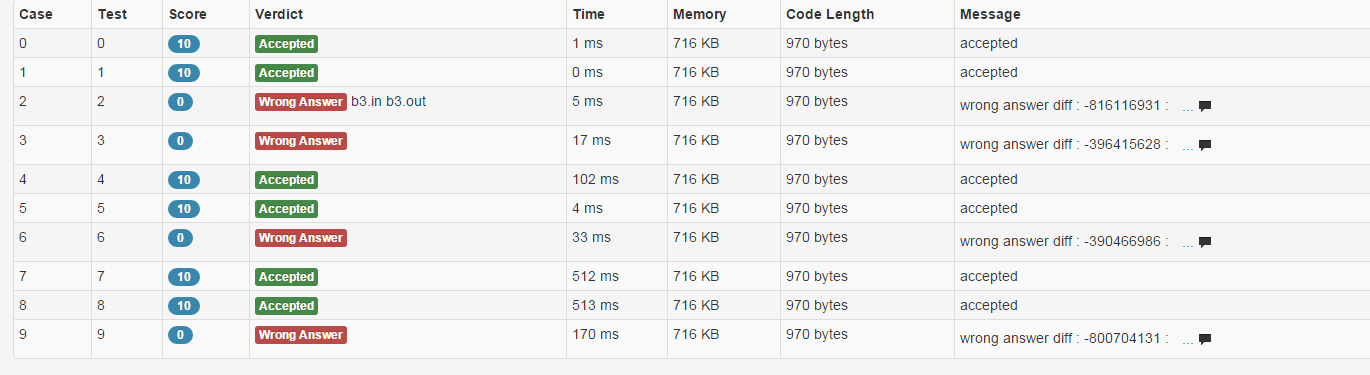
好吧。。。其实我不是很清楚原理，我只是知道不这样的话会出现负数，请读者仔细看看右边，是不是输出了很大的负数。。。。

#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;

const int maxn=17;
const int mod=1e9+7;
int n,m;
int a[maxn],b[maxn],s[maxn][maxn],a1[maxn];
ll F[1<<16];
void dfs(int x,int S,int S1,int l1,int l2)
{
    if (x==n)
    {
        int h=(l1&1?mod-1:1); 
        F[S]=(F[S]+1ll*h*s[l1][l2])%mod;
        return;
    }
    dfs(x+1,S,S1,l1,l2);//不加入S 
    ll ax=1<<a1[x];
    if (!(S1&ax)) dfs(x+1,S+(1<<x),S1+ax,l1+1,l2);//加入S1 
    dfs(x+1,S+(1<<x),S1,l1,l2+1);//加入S不加入S1
}
int main()
{
    freopen("bipartite.in","r",stdin);
    freopen("bipartite.out","w",stdout);
    scanf("%d%d",&n,&m);
    for (int i=0;i<=n-1;i++) {scanf("%d",&a[i]);b[i]=a[i];}
    sort(b,b+n);int len=unique(b,b+n)-b;//离散化 
    for (int i=0;i<n;i++)
        for (int j=0;j<=len;j++)
            if(a[i]==b[j]) {a1[i]=j;break;}
    for (int i=0;i<=n;i++)//预处理 
    {
        s[i][0]=1;int tmp=m-i;
        for (int j=1;j<=n;j++) s[i][j]=1ll*s[i][j-1]*tmp--%mod;
    }
    dfs(0,0,0,0,0);
    ll ans=0;
    for (int i=1;i<=(1<<n)-1;i++) ans=(ans+1ll*F[i]*i)%mod;//统计答案 
    printf("%lld",ans);
    return 0;
}