关于SVM数学细节逻辑的个人理解(二):从基本形式转化为对偶问题
第二部分:转化为对偶问题进一步简化
这一部分涉及的数学原理特别多。如果有逻辑错误希望可以指出来。
上一部分得到了最大间隔分类器的基本形式:
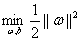
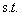
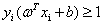 其中i=1,2,3...m
其中i=1,2,3...m
直接求的话一看就很复杂,我们还需要进一步简化。
这里就需要介绍拉格朗日乘子法。介绍它还是从最最简单的形式说起:
一.关于优化问题的最基本的介绍
优化问题这里面有很多东西,我先给出参考过的资料有,可以先看看这些资料自己总结一下,因为我觉得这部分内容很多人总结的都很好了:
①《支持向量机导论》的第五章最优化理论
②刚买的《统计学习方法》中的相关附录,不得不说这本书真的很棒
③《An Introduction to Optimization》这本书专门讲最优化的,如果要系统理解我觉得可以看看,但我只看了相关的部分
④知乎上的相关问题的回答。
⑤一些博客,下面会给具体链接
1.最简单的无约束优化问题
优化问题最简单的应该就是无约束的优化问题了吧。
很简单的举个例子,就比如 ,我们要求y在R上的最小值。
,我们要求y在R上的最小值。
一般的做法就是,先求导,然后导函数为0,就可以得到极小值点对应的x的值,代入后就得到对应的y的极小值,而这里极小值就是最小值。
然后高中其实我们就知道,即使无约束(即定义域为R),在很多情况下,极小值点也不一定是最小值点。因为可能会有很多个导函数为0的点(比如说正弦函数),所以此时我们的做法应该就是求出所有极小值点对应的y值,然后选择最小的。
这就是最简单的无约束优化问题,其实就是求导,让导数等于0。
2.带等式约束的优化问题
现在把问题变得复杂一点,我们考虑带等式约束的优化问题,下面举的例子和图片来自
我觉得这里已经解释的很不错了。
以后有时间会自己画好相应的图。
举个例子,现在的优化问题是:

等式约束: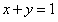
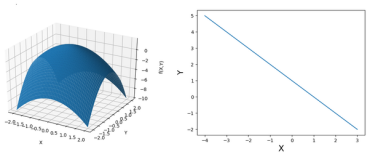
左边是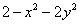 的图像,右边是
的图像,右边是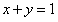 的图像。首先如果没有这个约束,那么我们很容易就可以得到当
的图像。首先如果没有这个约束,那么我们很容易就可以得到当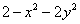 取最大值是在x=0且y=0处,做法就是对x和y分别求偏导,让偏导数为0,解出x和y。但是现在有了约束就不一样了。
取最大值是在x=0且y=0处,做法就是对x和y分别求偏导,让偏导数为0,解出x和y。但是现在有了约束就不一样了。
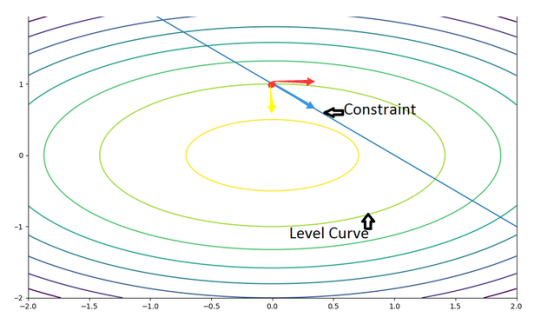
这个是目标函数的等高线图,等高线图我们原来看地图就接触到了,同一个曲线上的目标函数的值是一样的。其中我们也可以看到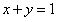 的约束。因为现在加入了
的约束。因为现在加入了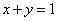 这个限制,那么x和y的变化只能被限制在这条直线(从这个角度看是直线,其实应该是
这个限制,那么x和y的变化只能被限制在这条直线(从这个角度看是直线,其实应该是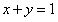 平面和
平面和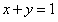 相交的曲线)上进行,而这条直线所确定的范围又被叫做可行域。
相交的曲线)上进行,而这条直线所确定的范围又被叫做可行域。
既然必须在这条直线上运行,那么我们可以先在直观上看在这条直线上运行如何影响原来目标函数的值。如果我们沿着这条直线从左上一直到右下,根据等高线我们可以知道目标函数值是先增大,然后减少。
可以具体的取图中的红点来看,假如有一个人沿着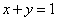 行走到这个红点了,那么可以用蓝色箭头来表示他在红点的速度,那么这个速度其实可以根据它所处的等高线,分为和等高线相切的速度分量(红色)和与等高线垂直的速度分量(黄色)。而这个和等高线相垂直的速度分量则决定了这个人的下一步的位置必然会改变目标函数的值。那么他运动到哪里就不会有这个“和等高线垂直的速度”呢?
行走到这个红点了,那么可以用蓝色箭头来表示他在红点的速度,那么这个速度其实可以根据它所处的等高线,分为和等高线相切的速度分量(红色)和与等高线垂直的速度分量(黄色)。而这个和等高线相垂直的速度分量则决定了这个人的下一步的位置必然会改变目标函数的值。那么他运动到哪里就不会有这个“和等高线垂直的速度”呢?
很明显,当他的速度正好和他所在位置的等高线相切时。此时不会有法线方向的速度了。
那他什么时候速度能和等高线相切呢?注意到这个人的“速度”方向其实一直被限制为这个直线的方向,所以相切发生在这个直线和等高线相切时。
(可能有些不太准确,但是为了直观上理解只能这样了)
此时我们就可以得到那个可以使目标函数值最大的点,就是找那个相切的点。
注意到,当约束函数的方向和等高线相切时,它们的梯度方向是共线的,即在那个点满足:
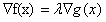 (
(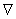 表示对自变量的梯度)
表示对自变量的梯度)
再加上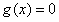 ,这两个条件其实就可以确定我们要求的点了。(因为要求解的未知量的个数和式子的个数相同)
,这两个条件其实就可以确定我们要求的点了。(因为要求解的未知量的个数和式子的个数相同)
上面就是当遇到等式约束的优化问题时,从直观上该如何解决,主要就是找到那个“相切点”。
那么我们如何用数学的方法求出满足这个条件的这个点呢?这就需要用到拉格朗日乘子法了。
(这里简单说一下只有一个等式约束时的情况)
对于优化问题:
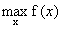
等式约束: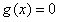 (注意等式约束要写成标准的
(注意等式约束要写成标准的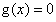 的形式,即等号右边为0)
的形式,即等号右边为0)
我们引入拉格朗日乘子λ,写出这个问题的拉格朗日函数:
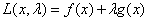
而我们的优化问题其实可以转化为:
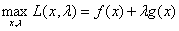
这个拉格朗日函数和我们之前说的
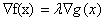
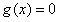
有什么关系呢?你可以试着让拉格朗日函数对每个变量都求偏导,并让偏导为0,就可以发现:
如果对x求偏导,我们就可以得到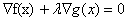
如果对λ求偏导,我们就可以得到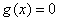
也就是说对拉格朗日函数求偏导,导数为0得到的结果其实就是我们之前需要的那两个条件:①梯度成正比②满足约束条件
拉格朗日乘子法其实就是把原来的有约束的优化问题转化为了无约束的优化问题,并且成功的把约束条件包含在了这个无约束的优化问题中。这就是我对于拉格朗日乘子法的理解。
(关于λ的符号问题,我在https://www.quora.com/What-is-an-intuitive-explanation-of-the-KKT-conditions这个人的回答里找到了这么一句话:拉格朗日乘子并没有符号限制,可能是因为拉格朗日乘子只是对于等式约束来说的,但是注意下面的KKT乘子却不是这样的)
到这里我们知道可以用拉格朗日乘子法来解决等式约束的优化问题。
但是你可能注意到在SVM的优化问题里,约束并不是个等式,而是一组不等式
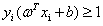 其中i=1,2,3...m
其中i=1,2,3...m
而我们之前介绍的是等式约束的优化问题,所以我们还必须要介绍带有不等式约束更一般的优化问题。
3.带不等式约束的优化问题
现在我们需要考虑最一般的情况,关于这部分内容我还没有理解的太透彻,我觉得知乎上彭一洋的答案在这部分写的很不错https://www.zhihu.com/question/58584814,可以参考一下。
在这里我只能说一说自己的理解了。
如果对于优化问题
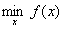
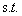
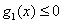
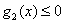
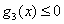
有三个不等式约束。对于这样的约束问题,它的最优解x*是一定需要满足KKT条件的。我先写出这些条件(下面这些条件再加上原始的约束条件其实就是整个KKT条件了,下面在更一般的情况下说),并在直观上说明为什么要这样。具体的证明在《An Introduction to Optimization》上有。
现在假设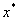 是这个约束问题的最优解,那么现在假设存在
是这个约束问题的最优解,那么现在假设存在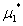 ,
,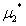 ,
,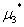 (KKT乘子)满足下面三个条件:
(KKT乘子)满足下面三个条件:
(1)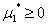 ,
,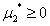 ,
,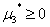
(2)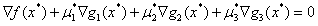
(3)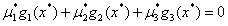
现在我们一个一个在直观上解释
条件(1)是说所有的KKT乘子需要大于等于0。关于这个问题我查了很多资料,但是没有一个让我觉得说清楚的解释。我个人把这个理解为一种规范?这个问题还需要思考,希望有人可以解释一下。
条件(2)表示目标函数在最优点的梯度可以用g1(x),g2(x)和g3(x)线性表示出来。这里看到是三个的线性组合之后的反方向,这是因为之前规定这个问题是最小化问题,根据Wiki上KKT条件的资料表明,如果是最大化问题,那么会是:
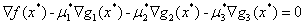
我们可以看下面这张图,可以看到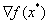 是可以由
是可以由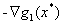 和
和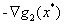 线性组合得到。但是发现
线性组合得到。但是发现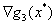 似乎并不参与
似乎并不参与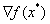 的计算,因为最小值点处并没有取到
的计算,因为最小值点处并没有取到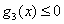 的等号,这个就需要条件(3)来解释了。
的等号,这个就需要条件(3)来解释了。
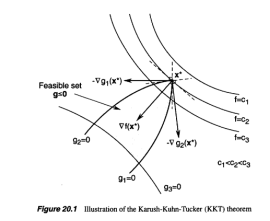
(图片来自于《An Introduction to Optimization》)
条件(3)比较重要,因为在最优点不是所有的不等式都取到了等号。取到等号的不等式约束,我们称它为积极约束,对于最优点点没取到等号的不等式约束,我们称它为非积极约束。而且因为对于每个μ和g(x),μ>=0,g(x)<=0,这就意味着如果条件(3)满足,那么其实可以得到对于每个每个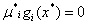 成立。对于非积极约束,因为它的g(x)不等于0,那么它对应的μ就必须为0。对于积极约束,它的KKT乘子可能非0也可能是0。后面就会知道条件(3)被叫做互补松弛条件
成立。对于非积极约束,因为它的g(x)不等于0,那么它对应的μ就必须为0。对于积极约束,它的KKT乘子可能非0也可能是0。后面就会知道条件(3)被叫做互补松弛条件
(这个要注意,不是说gi(x)=0了,它对应的KKT乘子就不能是0了,具体参考《An Introduction to Optimization》
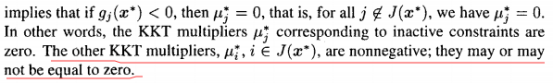
)
但是现在我只能通过给定的条件解释为什么要这样,却不能解释这些条件都是怎么推导出来的...
KKT条件是最优解的一个必要条件,在求解最优解时,通过解这些式子来求最优点。
4.更一般的优化问题,既有等式约束,又有不等式约束
而对于更一般形式的最优化问题,即既有等式约束,也有不等式约束:

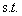
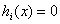 i=1,2,3,...m
i=1,2,3,...m
 i=1,2,3...k
i=1,2,3...k
现在令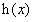 ,表示由
,表示由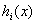 组成的列向量。然后令
组成的列向量。然后令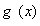 表示由
表示由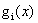 组成的列向量,然后让
组成的列向量,然后让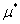 表示对应的KKT乘子组成的列向量,然后让
表示对应的KKT乘子组成的列向量,然后让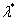 表示对应的拉格朗日乘子组成的列向量。
表示对应的拉格朗日乘子组成的列向量。
而且对于这个更一般的优化问题,在《支持向量机导论》的第五章(其他书上都还没找到)还可以找到它所对应的广义拉格朗日函数:
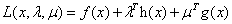
我现在可以写出这个优化问题对应的KKT条件(参考Wiki百科KKT条件的分类方式):
(1)Stationarity(平稳性..但是不知道为什么这么叫)
这里是最小化,所以对应的梯度条件是:
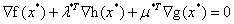
(注意这里的x可能有很多维,这时就是对每一维的偏导需要满足这个条件)
(2)Primal feasibility(优化问题自带的约束条件)
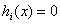 i=1,2,3,...m
i=1,2,3,...m
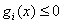 i=1,2,3...k
i=1,2,3...k
就是原来的已经存在的那两类约束,包括等式和不等式
(3)Dual feasibility(具体含义还不太明白)
就是KKT乘子必须满足的
对于任意的i,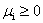 (注意到拉格朗日乘子并不需要这个条件)
(注意到拉格朗日乘子并不需要这个条件)
(4)Complementary slackness(互补松弛条件)
对于任意的i,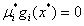 (条件4在理解后面的内容时挺重要的)
(条件4在理解后面的内容时挺重要的)
这么看一共有三个等式两个不等式,具体可以分为:①梯度要求②原始约束条件③KKT乘子需要满足大于等于0④互补松弛条件。
(这里可以把①和②分为一类,因为①和②都是对应的拉格朗日函数对变量求偏导为0)
5.自己动手推一推SVM优化问题中的KKT条件
OK,至此,优化问题的一部分数学知识就结束了,但是我们还是先继续学习对偶问题的相关知识,再回到最初的最大间隔分类器问题。
但是作为学完KKT条件的练习,我们可以尝试自己求一求之前的SVM问题的KKT条件!
上一部分最后的优化问题:
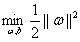
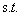
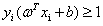 其中i=1,2,3...m
其中i=1,2,3...m
如果我们需要用KKT条件来解决这个问题的话,我们现在就可以写出它需要满足的KKT条件了,在此之前,先把约束不等式写成标准形式,并且注意到这里没有等式约束:
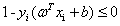 ,其中i=1,2,3..m
,其中i=1,2,3..m
假设对每个约束来说它的KKT乘子为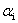 (很多SVM的书上都把α直接作为拉格朗日乘子,但是按照我目前的理解,感觉拉格朗日乘子是对于等式约束的,KKT乘子是对于不等式约束的,很多地方是不一样的,这里是不等式约束)
(很多SVM的书上都把α直接作为拉格朗日乘子,但是按照我目前的理解,感觉拉格朗日乘子是对于等式约束的,KKT乘子是对于不等式约束的,很多地方是不一样的,这里是不等式约束)
那么可以先写出对应的拉格朗日函数:
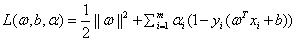
然后我们就可以先写出它需要满足的KKT条件为:
(1)梯度条件(对ω和b求偏导并等于0)
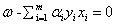
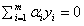
(2)自带的约束条件
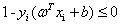 ,其中i=1,2,3..m
,其中i=1,2,3..m
(3)KKT乘子需要满足的
对于任意的i,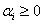
(4)最后就是松弛互补条件:
对于任意的i,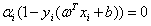
OK,可以自己推导一下KKT条件,是不是发现介绍SVM的书上的那些原来莫名其妙就给出来的KKT条件自己也能写出来呢。
很多书讲的太笼统了,还是有很多细节逻辑需要考虑的。
二.对偶问题的相关数学知识
我们还必须解释对偶问题相关知识。(可见SVM这里的数学知识太多了)
关于对偶问题的资料,我推荐:
①《支持向量机导论》第五章
②《统计学习方法》后面的附录
③博客写在SVM之前——凸优化与对偶问题
大家可以先自己看一看,关于对偶问题的内容在《统计学习方法》附录那里讲的是最清楚的个人认为。
1.原问题和对偶问题的定义
在求解最优化问题时,经常把原问题转化为对偶问题求解。
现在我们需要求解的优化问题为:
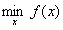
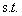
 i=1,2,3,...m
i=1,2,3,...m
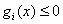 i=1,2,3...k
i=1,2,3...k
它对应的拉格朗日函数为:
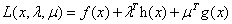
现在我们先定义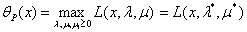 ,其中
,其中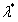 和
和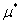 表示对于给定的
表示对于给定的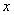 ,使得
,使得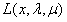 最大的那个
最大的那个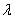 和
和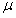 的取值,可以看出,这是一个关于
的取值,可以看出,这是一个关于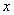 的函数。
的函数。
那么我们可以根据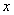 的不同取值范围得到:
的不同取值范围得到:
①当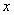 不满足之前规定的约束条件时,即假如对于某个i,
不满足之前规定的约束条件时,即假如对于某个i,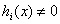 ,那么我可以通过改变对应的
,那么我可以通过改变对应的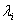 使得
使得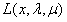 达到
达到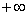 ,又或者对于某个j,
,又或者对于某个j,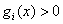 ,那么很明显我可以改变对应的
,那么很明显我可以改变对应的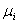 ,使得
,使得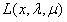 达到
达到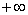 。
。
所以说,当x不满足某个约束条件时,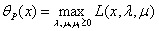 是
是
②而当x在满足约束条件的范围内时,因为对于每个i,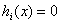 ,
,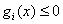 ,所以说此时的
,所以说此时的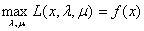 ,这个理解很重要
,这个理解很重要
那么我现在可以定义一个问题:
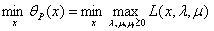
需要证明这个问题与原始的约束问题
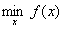
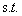
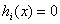 i=1,2,3,...m
i=1,2,3,...m
 i=1,2,3...k
i=1,2,3...k
等价。
证明这两个最优化问题等价,其实就是证明它们的优化目标和它们的约束条件是等价的。
这个也很容易证明:
①首先当x不满足约束条件时,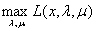 会达到
会达到 。那么在计算外层的关于x的最小化时,这个
。那么在计算外层的关于x的最小化时,这个 是不会影响到结果的。
是不会影响到结果的。
②而x满足约束条件时, ,和原始约束问题一样,都是在满足约束的情况下最小化
,和原始约束问题一样,都是在满足约束的情况下最小化 的。
的。
所以我们就把原始的约束问题表示为广义拉格朗日函数的极小极大问题。
我们定义原始问题的最优值为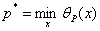
然后需要介绍其对偶问题,其实它的对偶问题很简单,就是把极小和极大的顺序颠倒一下即可。
我们先定义:
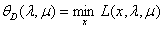 ,
,
然后考虑最大化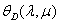
得到拉格朗日函数的极大极小问题,也就是原问题的对偶问题
即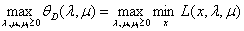 ,然后我们还定义对偶问题的最优值为:
,然后我们还定义对偶问题的最优值为:
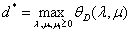
那么原问题的最优值和对偶问题的最优值有什么关系呢?
2.弱对偶定理
我们先介绍弱对偶定理,它证明了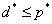
证明:对任意的x,λ,µ:
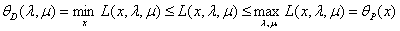
(第一个等号是定义,第二个小于等于号是因为min的定义,第三个小于等于号是因为max的定义)
也就是对于任意的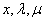 ,都有这样的
,都有这样的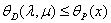 不等式成立。那么就说明了:
不等式成立。那么就说明了:
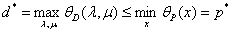
那么什么时候对偶问题的解和原问题的最优解可以相等呢?
3.对偶问题和原问题的最优解相等的充要条件
在《统计学习方法》里给出了定理:
对于原始问题和对偶问题,假设函数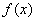 和
和 是凸函数,
是凸函数,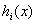 是仿射函数(按照我的理解就是形如
是仿射函数(按照我的理解就是形如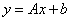 的函数),且不等式约束
的函数),且不等式约束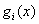 是严格可行的(严格可行即存在
是严格可行的(严格可行即存在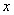 ,对于所有的i,都有
,对于所有的i,都有 <0),那么
<0),那么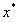 ,
,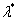 和
和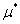 既是原始问题的最优解也是对偶问题的最优解的充要条件是:
既是原始问题的最优解也是对偶问题的最优解的充要条件是: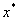 ,
,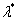 和
和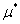 满足KKT条件。
满足KKT条件。
具体证明我没查,这个定理我觉得知道就好。
所以你可以看到KKT条件很重要。
4.自己推导SVM的对偶问题
接下来还是回到SVM的主线,我们需要来求一下SVM中遇到的问题的对偶形式是什么。
首先还是把原问题再列一下:
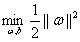
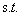
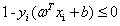 ,其中i=1,2,3..m
,其中i=1,2,3..m
拉格朗日函数:
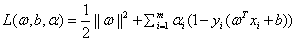
KKT条件为:
(1)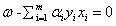
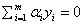
(2)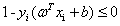 ,其中i=1,2,3..m
,其中i=1,2,3..m
(3)对于任意的i,
(4)对于任意的i,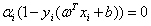
所以原问题写成极小极大问题的形式就是:
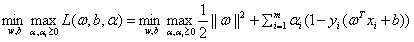
然后我们就可以求出它对应的极大极小问题形式,即对偶问题形式:
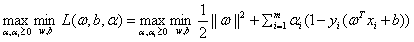
就是极大和极小换了下位置。
但是这样一换位置的好处就是,我们就可以先求解内部的
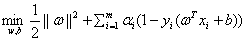 ,即通过求偏导,把
,即通过求偏导,把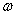 和
和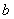 消去。
消去。
这就是很多书上莫名其妙的就求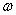 和
和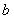 的偏导并消去的原因,就是因为只要满足之前说的那个充要条件,那么原问题就可以转化为对偶问题求解。
的偏导并消去的原因,就是因为只要满足之前说的那个充要条件,那么原问题就可以转化为对偶问题求解。
通过求偏导(之前已经求过了,在KKT条件里)并代入我们可以得到进一步只和有关的优化问题了,这一步的消去代入过程如下:

(最好还是自己推导一遍)
所以我们现在得到进一步的优化问题:
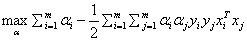
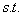
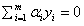
对任意的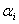 ,都有
,都有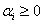
然后还需要满足之前说的KKT条件(可以翻看之前求出来的KKT条件),所以除了上面这两个约束外,还需要:
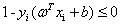 ,其中i=1,2,3..m 原始约束条件
,其中i=1,2,3..m 原始约束条件
对于任意的i,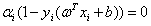 互补松弛条件
互补松弛条件
如果能够解出满足上面这个优化问题的最优解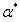 ,我们就可以根据这个
,我们就可以根据这个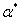 求解出我们需要的
求解出我们需要的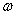 和b,所以我们把原来的关于
和b,所以我们把原来的关于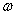 和b的最优问题转化为了求解
和b的最优问题转化为了求解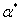 的问题
的问题
最后整理一下从SVM基本形式到它的对偶形式的逻辑过程:
①从SVM基本形式写出它的拉格朗日函数,这里需要知道拉格朗日函数的相关知识
②从它的拉格朗日函数形式转化为对偶形式,这里需要知道条件下对偶形式的最优解和原问题的最优解相等,也就需要理解KKT条件每一个的意义,并知道对于一般的约束问题如何写出它的KKT条件
而这里大多都是关于带约束的优化的相关数学知识,有时间可以系统的看一看《An Introduction to Opitimization》




 浙公网安备 33010602011771号
浙公网安备 33010602011771号