tsx 图论选讲

P6880 [JOI 2020 Final] 奥运公交 / Olympic Bus

题意

给定一个含有 $N$ 个点，$M$ 条边的有向图，每条边从 $U_i$ 指向 $V_i$，经过这条边的代价为 $C_i$。

在最开始时，我们可以翻转至多一条边，即让这条边从 $U_i\to V_i$ 永久变为 $V_i\to U_i$，并产生 $D_i$ 的代价。你要从点 $1$ 到点 $N$，再从点 $N$ 回到点 $1$，你想知道，通过翻转至多一条边，能得到的最小代价和为多少？

其中 $N\le 200,M\le 5e4$

思路

考虑翻转一条边会对最短路径造成什么影响，可以相当于添加一条边、删除一条边。

在添加一条边时，设新加的边为 $v\to u$，原 $1\to n$ 的最小代价为 $ans_1$，原 $n\to 1$ 的最小代价为 $ans_2$，从 $x$ 到 $y$ 的最短距离为 $dis_{x,y}$。那么此时能够产生的新代价为 $\min(ans_1+dis_{n,v}+dis_{u,1}+c_i+d_i,dis_{1,v}+dis_{u,n}+c_i+d_i+ans_2)$。（若 $dis_{1,v}$ 或 $dis_{n,v}$ 经过了 $u\to v$ ，那么答案一定不优，因为我们会经过这条边两次）

在删除一条边时，若原边不在 $1\to n$ 和 $n\to 1$ 的最短路径上，那么此时改变这条边时，原 $ 1 \leftrightarrows u,v \leftrightarrows n$ 的最短路径不变，仍然可以直接继承以前的答案 $ans_1,ans_2$。但是若处于最短路径上，此时原答案会改变，所以我们还是需要再跑一遍最短路。考虑到最短路径上只会最多有 $2n$ 条边，因此，这样的时间复杂度为 $n\times m+n\times (m+n)\times \log(n+m)=n^3$ 。

AT_arc107_f [ARC107F] Sum of Abs

题意

有一个包含 $N$ 个顶点和 $M$ 条边的简单无向图，每个顶点 $i$ 上写有两个整数 $A_i, B_i$。

可以选择删除 $0$ 个或多个顶点。删除顶点 $i$ 的代价为 $A_i$，与被删除顶点相连的边也会被同时删除。删除完顶点后，得分的计算方式如下：

总得分等于所有连通分量得分的总和。
某个连通分量的得分为该分量内所有顶点的 $B_i$ 之和的绝对值。

收益定义为 $($总得分 $-$ 删除顶点的总代价$)$，求出最大收益。

其中 $N\le 300,M\le 300$

思路

我们最想做到的肯定是负数在同一个连通分量里，正数在同一个连通分量里。但这种情况不一定是最优方案。直接删点我们发现连通性不好判断，所以可以考虑 时间倒流，先花费全部代价把所有点都删掉，再一个一个加入。

此时加入一个点 $i$ 的代价就变到了 $a_i+b_i$ 或 $a_i-b_i$（因为此时若所处集合总权值 $<0$ ，那么加入一个点的代价即为 $-b_i$ ）。计前面的点为 $i^+$ ，后面的点为 $i^-$ 。

显然两个点不能都被选入集合。这样的形式很像独立集。

一个集合内的点要么全为 $i^+$ ，要么全为 $i^-$，这个限制依然是不好考虑的，可以考虑如何转化成上面的限制。对于一条边 $u\to v$ ，有限制 $u^+\nrightarrow v^-$ ，$u^-\nrightarrow v^+$ ，与上面同理。

二分图最小权点覆盖集

点覆盖集指选择一些点，这些点能够与图中的所有边连接。可使用网络流最小割来处理，具体的，若一个点的权值 $\le0$ ，显然可以直接选择该点。对于剩下的点，让 $s$ 向 $A$ 集合的点连一条权值为点权的边，$A$ 到 $B$ 连一条无穷大的边，$B$ 向 $t$ 连一条权值为点权的边，此时在这张图中求最小割即可求出答案，正确性显然。

二分图最大权独立集

经过上面的点覆盖集，那么我们若不选这些位于点覆盖集的点，那么剩下的点一定可以组成一个点独立集（任意两点之前都不存在边），证明可以考虑我们若删去和这些点独立集内的点相连的边，那么此时所有边都会被删除。那么此时的最大权独立集即为总点权 $-$ 最小权点覆盖集。

那么对于原题目，此时我们的总点权为 $2\times \sum a_i$ ，让所有的 $i^+$ 向 $i^-$ 连一条无穷大的边，$s$ 向 $i^+$ 连一条点权边， $i^-$ 向 $t$ 连一条点权边，对于一条边 $u\to v$ 同理连不同号之间的无穷大边，此时在原图中求最小割即为最小权点覆盖集的大小，此时用 $2\times \sum a_i-$ 该权值即为最大权独立集大小，再减去一开始删点的代价。

如果 $i^+$ 和 $i^-$ 都被删去了，此时的代价变为 $2a_i-(a_i+b_i)-(a_i-b_i)-a_i$ ，可以发现正好等于删去该点的代价。

uoj605 知识网络

题意

一张图上有 $n$ 个点，其中每个点都有一个标签，标签总数为 $k$ ，求出全源最短路，输出每一种路径长度的路径条数。

其中 $n\le 5e4,k\le 150$

思路

最暴力的做法是把所有点都跑一遍最短路，时间复杂度 $O(n\times (n+m))$

数据范围提示我们去考虑每一个标签内的情况，把该标签内所有的点都与其他非此标签点求出最短距离，显然的是，标签内的点到其他任意一个点的最短路径距离之差不会超过 $1$ 。

所以可以利用这一特性，对于每一个点都暴力求出该标签内有多少个点能够在最短路DAG上到达他。不妨把所有该标签的点称为 关键点 。具体的，我们可以拿 bitset 来实现这个过程，当 $x$ 是 $y$ 在最短路径图上的前驱时，把能够到达 $x$ 的所有点继承到 $y$ 点上。

关于空间限制 $256Mb$ ，我们可以选择把一个标签内的点分多次跑完。

P3227 切糕

题意

给定一个 $p*q*r$ 的长方体，每个 $1*1*1$ 方块上都有一个权值 $v_{i,j,k}$，现在要对所有的第 $x$ 行第 $y$ 列的方块钦定一个高度 $h(x,y)$，满足相邻四个 $h(x,y)$ 的绝对值之差不得超过 $D$，求出能够实现的所有权值之和中最小值。

其中 $p,q,r\le 40$

思路

可以转化成网络流模型，显然要用最小割处理。对于一个点 $(i,j,k)$，我们显然可以连出这样几条边

$(i,j,k)\to (i,j,k+1)$，边权为 $v_{i,j,k}$
$(i,j,k)\to(i,j,k-1)$，边权为 $\inf$
$(i,j,k)\to (i+1,j,k-D)\dots$，边权为 $inf$
$S\to (i,j,1)$ ，边权为 $inf$
$(i,j,r)\to T$ ，边权为 $v_{i,j,r}$

其中，第一类边显然是方便我们进行最小割，第二类边是为了控制我们只能割掉一条链上的一条边，第三类边是为了控制绝对值之差。

但是，为什么第二类边能够控制绝对值之差？

引理：我们若割掉一条边 $u\to v$，那么肯定有 $s\to u\to v\to t$ 。

那么我们就可以考虑下面的这张图了：

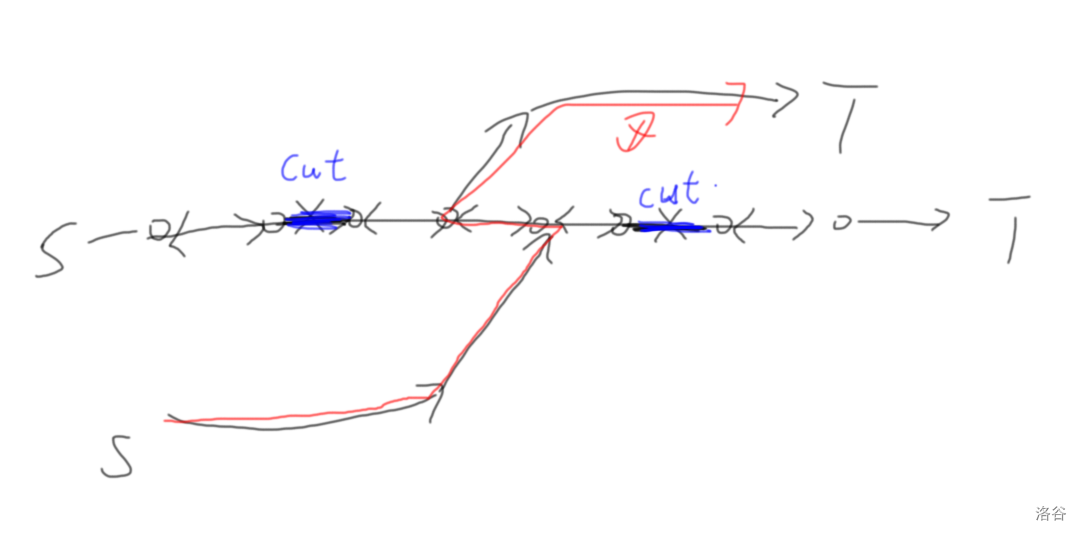
在这张图上，我们在同一条链上割掉了两条边 $x_1\to y_1$， $x_2\to y_2$，那么按照上面的引理，$S$ 能到达 $x_2$ ，$T$ 能到达 $y_1$ ，我们的第二类边就可以直接让 $S\to T$ 了，显然不合法。

P5332 [JSOI2019] 精准预测

题意

目前，火星小镇上有$n$个居民。有 $m$ 个预测关于这些居民在接下来$T$个时刻的生死情况，每条预测都是如下两种形式之一：

$0$ $t$ $x$ $y$：在$t$时刻，如果$x$是死亡状态，那么在$t+1$时刻，$y$是死亡状态。
$1$ $t$ $x$ $y$：在$t$时刻，如果$x$是生存状态，那么在$t$时刻，$y$是死亡状态。

希望为每个人$k$计算

\[\sum_{1 \leq i \leq n,i \neq k} \operatorname{Live}(k,i) \]

其中 $\operatorname{Live}(i,j)=1$ 表示编号为$i$和$j$的人有可能同时在第 $T+1$ 时刻处于生还状态，否则$\operatorname{Live}(i,j)=0$。注意人是不能够复活的。一个人可能在时刻$1$就处于死亡状态，也有可能有预测未覆盖的死亡情况发生。

其中 $1\le T\le 1e6,1\le n\le 5e4,1\le m\le 1e5$

思路：

一眼想到 2-sat 问题，考虑如何建图，设 $p_{i,j,0/1}$ 表示第 $i$ 个人在 $j$ 时刻死亡/生存。

最原本的，我们存在边 $p_{x,t,1}\to p_{x,t-1,1},p_{x,t,0}\to p_{x,t+1,0}$

对于 $0$ 号操作，我们有建图：$p_{x,t,0}\to p_{y,t+1,0}$

对于 $1$ 号操作，我们有建图：$p_{x,t,1}\to p_{y,t,0}$

但是此时的空间复杂度是 $O(nT)$ 的，显然不可接受

我们发现可以只保留必要的一些节点，此时的空间复杂度即为 $O(m)$ 的，对于每个点都去从 $p_{i,0,1}$ 遍历整张图，bitset 暴力维护能够到达的所有节点，此时的复杂度即为 $O(\frac{nm}{w})$ 。

注意，我们可能会出现 必死节点，即从 $p_{i,0,1}$ 开始遍历能够遍历到 $p_{i,j,0}$，他必定死亡。

AT_arc176_e [ARC176E] Max Vector

题意

给定两个长度为 $N$ 的正整数序列 $X=(X_1,X_2,\dots,X_N), Y=(Y_1,Y_2,\dots,Y_N)$。

另外，还给定 $M$ 个长度为 $N$ 的正整数序列。第 $i$ 个正整数序列为 $A_i = (A_{i,1},A_{i,2},\dots,A_{i,N})$。

你需要依次对 $i=1,2,\dots,M$ 进行如下两种操作之一。对于每个 $i$，可以独立选择要执行哪种操作。

对所有满足 $1 \le j \le N$ 的整数 $j$，将 $X_j$ 替换为 $\max(X_j, A_{i,j})$。
对所有满足 $1 \le j \le N$ 的整数 $j$，将 $Y_j$ 替换为 $\max(Y_j, A_{i,j})$。

请你求出操作结束后 $\sum_{j=1}^{N} (X_j + Y_j)$ 的最小值。

其中 $N\le 10$， $M,V\le 500$

思路

一般的 $dp$ 显然不好处理，考虑网络流最小割。

可以考虑和切糕类似的处理方式，把每一个点转化成一条链，具体的，我们对这 $2N$ 个数字分别维护一条长为 $V$ 的值域链，$X$ 链的权值从大到小，$Y$ 链的权值从小到大，边权均为前一个点的点权。

对于一次操作，我们可以考虑如何分别限制住所有的 $X$ 链和 $Y$ 链，可以让所有的 $X_{i,a_{j,i}}$ 向每一个 $Y_{i,a_{j,i}}$ 连一条无穷大的边，反之同理。此时我们考虑若存在任意一个 $X_{i}$ 取得了比 $a_j$ 要小的权值，那么若 $Y_i $ 同样取得比 $a_j$ 小的权值，此时必定无法构成一组割。

但是直接连边不太正确，因为我会把这 $N$ 个点分开考虑是去让 $X$ 替换或让 $Y$ 替换，有没有方法可以同时考虑到呢？

可以让所有的 $X$ 点全部连接到一个新开的点上，这个新开点再去连接到所有 $Y$ 节点上，这样就可以独立限制 $Y$ 和 $X$ 了。

CF875F Royal Questions

题意

有 $N$ 个王子，$M$ 个公主，这 $M$ 个公主都各自携带了嫁妆，都有中意的两个人选，求出在一夫一妻制下，能够收获的嫁妆最大价值。

其中 $n,m\le 2e5$

思路

一眼二分图最大权匹配，直接TLE。

转化题意，我们此时相当于给原图中的一些点定向，使其王子间生成基环树或树，这个过程很像 $kruskal$，所以我们考虑贪心，可以直接仿照 $kruskal$ 进行选边操作，若此时合并时两人不在同一集合中，那么直接合并即可，否则要判断当前的联通块是否已经变成了一颗基环树。

AT_arc092_d [ARC092F] Two Faced Edges

题意

给定一个包含 $N$ 个顶点和 $M$ 条边的简单有向图。

对于每一条边，判断如果将该边反向，图中的强连通分量的个数是否会发生变化。

其中 $n\le 1e3,m\le 2e5$

思路

考虑一条边 $u\to v$ 在什么时候会对强连通分量造成影响：

若原图中存在一条不含边 $(u,v)$ 的 $u\to v$ 的路径。
若原图中存在一条 $v\to u$ 的路径。

当这两个条件仅满足其一时答案必定改变，这是显然的。那我们只需要求出是否会存在这样的边即可。

我们此时二号条件是好判断的，可以 $O(n(n+m))$ 的求出，现在考虑一号条件。我们若直接在遍历边的时候尝试复杂度为 $O(m(n+m))$ 必定超时，所以尝试预处理。转化题意，我们此时求的即是 $(u,v)$ 是否是 $u\to v$ 的必经边，那么我们可以先正序跑一遍连接 $u$ 的边，再倒序跑一遍连接 $u$ 的边，那么此时两次遍历到 $v$ 的边的编号若不同，那么 $(u,v)$ 必然不是必经边。

CF1697F Too Many Constraints

题意

你需要构造一个由 $n$ 个整数组成的数组 $a$，其中每个元素都在 $1$ 到 $k$ 之间。

该数组必须是非递减的，还有一些额外的限制条件，每个限制条件属于以下三种类型之一：

$1~i~x$：$a_i$ 不能等于 $x$；
$2~i~j~x$：$a_i + a_j$ 必须小于等于 $x$；
$3~i~j~x$：$a_i + a_j$ 必须大于等于 $x$。

请构造任意一个满足所有限制条件的非递减数组，或者报告不存在这样的数组。

其中 $n\le 2e4,m\le 2e4,k\le 10$

思路

~~一眼差分约束~~ （无法处理 $\ne x$）

~~$k$ 这么小，最小割！~~ （$nk$ 的总数到达了 $2e5$ 级别，不可能）

考虑 2-sat，那么此时最显然的想法是设布尔变量 $z_i=1$ 表示 $=i$ ，但是我们显然无法控制只有一个 $z_i=1$，所以我们考虑更改状态。设 $z_i=1$ 表示 $\ge i$ ，所以此时我们显然建图是简单的，但是非常麻烦……。

Hall 定理

内容

设二分图的左右两部分点数分别为 $x,y(x\le y)$ ，定义 完备匹配 即为左部的 $x$ 个点都能成为匹配点。

一个二分图存在完备匹配的 充要条件 为：

对于左部点能够形成的所有子集，与其相连的右部点集的大小不小于左部点集的大小。

形式化的说：

\[\forall S\subseteq V,|N(S)|\ge|S| \]

推论

任意一个二分图 $(V,E)$ 的最大匹配为

\[|V|-\max_{S\subseteq V}(|S|-|N(S)|) \]

AT_arc076_d [ARC076F] Exhausted?

题意

有 $M$ 把椅子排成一条数轴，编号为 $i$ 的椅子位于坐标 $i$。

有 $N$ 名高桥君，第 $i$ 个人希望坐在坐标不大于 $L_i$ 或者不小于 $R_i$ 的椅子上。

你可以在任意实数坐标添加椅子。请计算最少需要添加多少把椅子才能让每个人都有椅子。

其中 $N,M\le 2e5$

思路

此时求的就是二分图最大匹配，可使用上面的 Hall 定理 进行求解。考虑如何维护，对于一个点集 $S$ 来说，求出他们能坐的椅子的并是不好求的，但是求出不能坐的椅子的交是好求的。那么我们需要维护的就是 $\max_{S\subseteq V}(|S|-(m-\text{不能坐的椅子数量}))$ 。

由于他们不能坐的椅子的交一定是一个区间，所以我们不妨固定区间左端点，动态维护右端点的最优值。

具体的，考虑扫描线，我们按左端点从小到大加入区间，对于一个右端点到 $M$ 我们区间加 $1$ ，表示若选择该点作为右端点，那么点集加一最优。那么我们此时只要求出右端点最大值即可。

AT_agc034_d [AGC034D] Manhattan Max Matching

题意

给定一张二维网格。

首先，进行了 $N$ 次放置红球的操作。第 $i$ 次操作时，在坐标 $(RX_i, RY_i)$ 处放置了 $RC_i$ 个红球。

接着，进行了 $N$ 次放置蓝球的操作。第 $i$ 次操作时，在坐标 $(BX_i, BY_i)$ 处放置了 $BC_i$ 个蓝球。

接下来，将所有红球和蓝球两两配对，共组成 $S$ 对。每个球恰好属于一个配对。对于坐标 $(rx, ry)$ 的红球和坐标 $(bx, by)$ 的蓝球组成的配对，其得分定义为 $|rx-bx| + |ry-by|$。

求出配对得分总和的最大值。

其中 $N\le 1000,RC_i,BC_i\le 10$

思路

考虑一个球自己对答案的贡献，显然可以发现只有四种可能：

$rx+ry$
$rx-ry$
$-rx+ry$
$-rx-ry$

其中，蓝球的 $1$ 贡献需要与红球的 $4$ 贡献相等……

这启示我们独立考虑每个点的贡献，可以考虑费用流，此时我们建立 $4$ 个新点 $i_1,i_2,i_3,i_4$ 分别表示红球的贡献方式为 $1$ 且蓝球的贡献方式为 $4$，……。让每个蓝球向 $i_1,i_2,i_3,i_4$ 连一条流量为点数，费用为贡献代价的边，跑费用流即可解决。

UOJ61 怎样更有力气

题意

一个 $n$ 个点的图，图初始无边。给定一颗由这 $n$ 个点组成的树，有 $m$ 个时间段，每个时间段会指定树上的两个点 $u,v$，可以在树上 $u\to v$ 的简单路径上选取任意多个点对，在图上的点对之间建边，每次单个点对建边代价为 $w$。

与此同时，给定 $k$ 个限制关系 $t,u,v$，表示在时间 $t$ 时不能在 $u,v$ 之间建边。

求图联通的最小代价

其中 $n,m,k\le 3e5$

思路

考虑暴力：

可以发现这是一个求最小生成树的过程，按 $w$ 从小到大排序，每次把 $u\to v$ 路径上的所有点全部拉出来，两两之间判断是否能够连边，时间复杂度 $O(mn^2)$。

寻找性质：

考虑限制什么时候才会影响建边结果，若在一条点数为 $n'$ 的链上加边，有 $p$ 条限制，那么当 $n'-1> p$ 的时候一定可以把这条链所有点直接建边，使其联通。不难证明正确性（$p$ 条限制全部集中于一点 $x$）。

考虑剩余 $p\ge n'-1$ 的情形如何优化，对于限制建图，那么此时可以考虑固定一点 $x$，剩余的能在原图上建边的点一定是不与 $x$ 直接相连的点（设点集为 $V_1$），我们就可以直接让这样的点与 $x$ 建边。

剩下与 $x$ 直接相连的点（设点集为 $V_2$），我们需要单独考虑他们是否能够建边：

与 $V_1$ 内的点建边：与 $V_1$ 的限制个数不得等于 $|V_1|$
与 $V_2$ 内的点建边：暴力遍历，判断是否两两之间不存在限制。

考虑此时的时间复杂度：显然只需考虑 $p\ge n'-1$ 的情况，化简后均摊即可发现这样的链的总点数不会超过 $K$ ，那么对于 $V_1$ 与 $x$ 建边可以之间暴力遍历 $V_1$。

那么我们现在想要做到的就是最小化与 $x$ 直接相连的点，显然直接取度数最小的点即可，这样的点的度数不会超过 $\max\frac{p}{n'}=\sqrt p$ ，显然 $1,2$ 操作都可以直接暴力遍历，复杂度为 $O(\sqrt p+(\sqrt p)^2)=O(p)$ 的。

那么此时瓶颈在于排序，时间复杂度为 $O(m\log m+k)$

UOJ32 跳蚤公路

题意

给定一张 $n$ 个点 $m$ 条边的有向图，每次走过一条边都要花费 $w_i$ 的代价（可以为负数），边上有三种颜色：红色、白色、绿色。

现在需要钦定一个数 $-10^{30}<x<10^{30}$ ，让所有的红色公路的过路费增加 $x$ ，所有的绿色公路的过路费减少 $x$ 元。

对于每个点 $u$ ，求出满足图中从$1$ 到 $u$ 的路径中没有负环的整数 $x$ 的数量。

其中 $n\le 100,m\le 10000$

思路

考虑如何拆分一条路径上的新贡献，因为 $x$ 一定，所以我们一定可以把一条路径上的总价值记为 $val=kx+b$，其中 $b$ 为原边权。因为我们现在的目标是对于任意一条路径都有 $kx+b\ge 0$，即 $x\ge -\frac{k}{b}$。为了求出 $x$ 的交集，所以求出这样的 $b$ 的最小值一定是不劣的。所以我们此时需要做的就是求出这样路径的 $x$ 的系数，以及 $b$ 的最小值。

现在我们的问题就转化到了最短路上，考虑最短路求负环的方式：

考虑此时在最短路的过程中需要记录哪些状态？

显然我们必须要记录的是节点 $u$，$x$ 前的系数 $k$，若使用 $Floyd$ ，我们此时的时间复杂度变为 $n^5$，无法接受。

考虑 $bellman-ford$，$f_{i,u,k}$ 表示从 $1$ 到 $u$ 经过的边数不超过 $i$ 的情况下 $x$ 前的系数为 $k$ 的 $b$ 值。那么此时不存在负环的判断方法即为

\[\min\{k_1x+f_{n,u,k_1}\}\ge min\{k_2x+f_{n-1,u,k_2}\} \]

考虑如何拆式，先固定 $k_1$，得到 $k_1x+f_{n,u,k_1}\ge \min\{k_2x+f_{n-1,u,k_2}\}$，此时存在负环的 $x$ 的解集即为该式解集的交集 $\cap$。

我们再拆开不等式的另一边，得到 $k_1x+f_{n,u,k_1}\ge k_2x+f_{n-1,u,k_2}$，此时的上式解集即为该式解集的并集 $\cup$。

更直观的方法：

\[\forall k_1\exists k_2,\text{都有 }k_1x+f_{n,u,k_1}\ge k_2x+f_{n-1,u,k_2} \]

所以此时我们对于每个 $x$，通过枚举 $k_1,k_2$，即可求出 $x$ 的解集。

时间复杂度 $O(n^4)$ ，瓶颈在于 $bellman-ford$

注意：此时我们解 $2$ 式得到的解集会是这种情况：

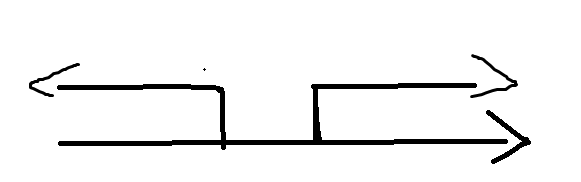
直接对于这种解集求交显然是不好求的，我们不妨把它转化成补集求并

posted @ 2025-09-22 15:19 xtp 阅读(12) 评论(0) 收藏举报

刷新页面返回顶部

xxmbb