Burgers' Equation - Finite Volume

  • 有限体积法引入:
    考虑如下守恒型方程:
    \begin{equation}
    \frac{\partial u}{\partial t} + \frac{\partial f}{\partial x} = 0
    \label{eq_1}
    \end{equation}
    对第$i$个控制体进行积分:
    \begin{equation}
    \begin{split}
    & \quad\int_{i - 1/2}^{i + 1/2} \frac{\partial u}{\partial t} \mathrm{d}x + \int_{i - 1/2}^{i + 1/2} \frac{\partial f}{\partial x} \mathrm{d}x = 0   \\
    \Rightarrow & \quad\frac{\partial}{\partial t}\int_{i - 1 / 2}^{i + 1 / 2}u\mathrm{d}x + f_{i + 1/2} - f_{i - 1/2} = 0   \\
    \Rightarrow & \quad\frac{\partial u_i}{\partial t} = \frac{1}{\Delta x}(f_{i - 1/2} - f_{i + 1/2})
    \end{split}
    \label{eq_2}
    \end{equation}
    左侧时间微分$\frac{\partial u_i}{\partial t}$采用Runge-Kutta方法处理之, 右侧单元界面处通量值$f_{i - 1/2}$、$f_{i + 1/2}$采用Godunov scheme处理之.
  • Runge-Kutta方法:
    考虑如下ODE:
    \begin{equation}
    \frac{\mathrm{d}u_i}{\mathrm{d}t} = g(t, u_i)
    \label{eq_3}
    \end{equation}
    经典RK4给出如下数值解:
    \begin{equation}
    u_{i}^{n+1} = u_{i}^{n} + \frac{h}{6}(k_1 + 2k_2 + 2k_3 + k_4)
    \label{eq_4}
    \end{equation}
    其中:
    \begin{gather*}
    k_1 = g(t^n, u_i^n)   \\
    k_2 = g(t^n + \frac{h}{2}, u_i^n + \frac{h}{2}k_1)   \\
    k_3 = g(t^n + \frac{h}{2}, u_i^n + \frac{h}{2}k_2)   \\
    k_4 = g(t^n + h, u_i^n + hk_3)
    \end{gather*}
  • Godunov scheme:
    Part Ⅰ: Godunov flux
    purpose: upwind scheme
    取$u_l$、$u_r$分别为单元界面左右两侧之u值, 则
    \begin{equation}
    f =
    \begin{cases}
    \min f(u), & \text{if } u_l < u_r   \\
    \max f(u), & \text{if } u_l > u_r
    \end{cases}
    \label{eq_5}
    \end{equation}
    其中, $u \in [\min\{u_l, u_r\}, \max\{u_l, u_r\}]$.
    Part Ⅱ: reconstruction
    purpose: ①. monotonicity; ②. high accuracy
    考虑单元界面$i + 1/2$, 则
    \begin{align}
    u_{i + 1/2}^l = u_i + \frac{u_i - u_{i-1}}{2}\cdot \phi (r), & \quad\text{where } r = \frac{u_{i + 1} - u_i}{u_i - u_{i - 1}}   \\
    u_{i + 1/2}^r = u_{i+1} + \frac{u_{i+1} - u_{i+2}}{2}\cdot \phi (r), & \quad\text{where } r = \frac{u_i - u_{i+1}}{u_{i+1} - u_{i+2}}
    \label{eq_6_7}
    \end{align}
    其中, $\phi (r)$为限制器函数, 取值范围如下:
    \begin{equation}
    \phi (r)
    \begin{cases}
    = 0, &\quad\text{if }r \leq 0   \\
    \leq 2r, &\quad\text{if } 0 < r < 1   \\
    = 1, &\quad\text{if }r = 1   \\
    \leq 2, &\quad\text{if } r > 1
    \end{cases}
    \label{eq_8}
    \end{equation}
    常见2阶精度限制器函数如下:
    \begin{equation}
    \phi_{\text{superbee}}(r) = 
    \begin{cases}
    0, &\quad\text{if }r \leq 0   \\
    2r, &\quad\text{if }0 \leq r \leq 1/2   \\
    1, &\quad\text{if }1/2 \leq r \leq 1   \\
    r, &\quad\text{if }1 \leq r \leq 2   \\
    2, &\quad\text{if } r \geq 2
    \end{cases}
    \label{eq_9}
    \end{equation}
    \begin{equation}
    \phi_{\text{minmod}}(r) = 
    \begin{cases}
    0, &\quad\text{if }r \leq 0   \\
    r, &\quad\text{if }0 \leq r \leq 1   \\
    1, &\quad\text{if }r \geq 1
    \end{cases}
    \label{eq_10}
    \end{equation}
    \begin{equation}
    \phi_{\text{Van Leer}}(r) = 
    \begin{cases}
    0, &\quad\text{if }r \leq 0   \\
    \frac{2r}{1 + r}, &\quad\text{if }r \geq 0
    \end{cases}
    \label{eq_11}
    \end{equation}
  • 一维Burgers方程初边值问题:
    本文拟采用Van Leer限制器, 求解如下Burgers' equation:
    \begin{equation*}
    \frac{\partial u}{\partial t} + \frac{\partial u^2 / 2}{\partial x} = 0, \quad x \in \Omega = [0, 1], t \in [0, 0.5]
    \end{equation*}
    初边值条件如下:
    \begin{equation*}
    \begin{cases}
    u(x, 0) = \sin(2\pi x), & \quad x \in \Omega   \\
    u(x, t) = 0, & \quad x \in \partial\Omega, t \in [0, 0.5]
    \end{cases}
    \end{equation*}
  • 代码实现:
     
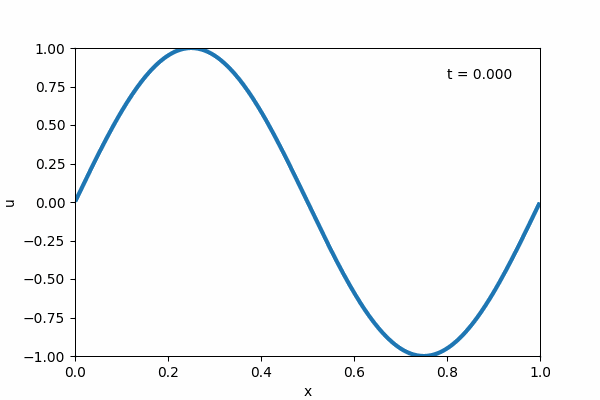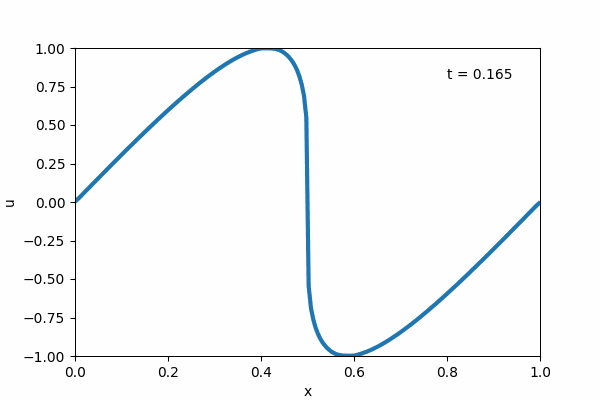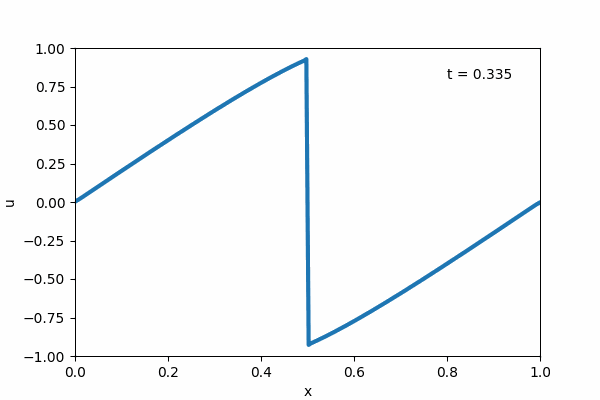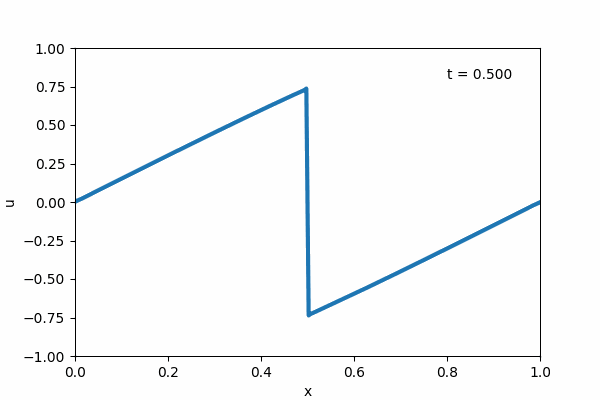
      1 # Burgers' equation之求解 - 有限体积法
  2 # 1. monotonicity
  3 # 2. high accuracy
  4 
  5 import numpy
  6 from matplotlib import pyplot as plt
  7 from matplotlib import animation
  8 
  9 
 10 # Runge-Kutta方法
 11 def RK4(func, t, u, h):
 12     '''
 13     func: 导函数func(t, u)
 14     t: 当前时刻
 15     u: t时刻之u值
 16     h: 下一时刻与当前时刻之时间差
 17     '''
 18     half_h = h / 2
 19 
 20     k1 = func(t, u)
 21     k2 = func(t + half_h / 2, u + half_h * k1)
 22     k3 = func(t + half_h / 2, u + half_h * k2)
 23     k4 = func(t + h, u + h * k3)
 24 
 25     uNew = u + h / 6 * (k1 + 2 * k2 + 2 * k3 + k4)
 26     return uNew
 27 
 28 
 29 # Burgers' equation求解
 30 class BurgersEq(object):
 31 
 32     def __init__(self, nx=100, nt=100):
 33         self.__nx = nx                               # x轴网格数
 34         self.__nt = nt                               # t轴网格数
 35 
 36         self.__init_grid()                           # 网格初始化
 37 
 38 
 39     def get_solu(self):
 40         UList = list()
 41 
 42         U0 = self.__calc_U0()
 43         UList.append(U0)
 44         for t in self.__T[:-1]:
 45             Uk = self.__calc_Uk(t, U0)
 46             UList.append(Uk)
 47             U0 = Uk
 48             
 49         return self.__T, self.__X, UList
 50 
 51 
 52     def __calc_Uk(self, t, UOld):
 53         UNew = RK4(self.__calc_dUdT, t, UOld, self.__ht)
 54         return UNew
 55 
 56 
 57     def __calc_dUdT(self, t, UOld):
 58         U = self.__fill_U_boundary(UOld)             # u边界填充
 59         UHL = self.__calc_UHalfLeft(U)               # 不含首尾边界
 60         UHR = self.__calc_UHalfRight(U)              # 不含首尾边界
 61         FH = self.__get_GodunovFlux(UHL, UHR)        # 不含首尾边界
 62         F = self.__fill_F_boundary(FH)               # flux边界填充
 63         dUdT = (F[:-1] - F[1:]) / self.__hx
 64         return dUdT
 65 
 66 
 67     def __fill_F_boundary(self, FH):
 68         tmpFH = numpy.hstack(([0], FH, [0]))
 69         return tmpFH
 70 
 71 
 72     def __get_GodunovFlux(self, UHL, UHR):
 73         FH = numpy.zeros(UHL.shape)
 74         FHL = UHL ** 2 / 2
 75         FHR = UHR ** 2 / 2
 76         FH[UHL >= UHR] = numpy.max((FHL, FHR), axis=0)[UHL >= UHR]
 77         FH[UHL < UHR] = numpy.min((FHL, FHR), axis=0)[UHL < UHR]
 78         FH[(UHL < UHR) & (UHL * UHR < 0)] = 0
 79         return FH
 80 
 81 
 82     def __calc_UHalfRight(self, U):
 83         Ui = U[1:-2]
 84         UiPlusOne = U[2:-1]
 85         UiPlusTwo = U[3:]
 86 
 87         tmpItem = UiPlusOne - UiPlusTwo
 88         UHR = list()
 89         for idx, ele in enumerate(tmpItem):
 90             if ele == 0:
 91                 UHR.append(UiPlusOne[idx])
 92             else:
 93                 r = (Ui[idx] - UiPlusOne[idx]) / ele
 94                 phi = self.__get_limitor(r)
 95                 UHR.append(UiPlusOne[idx] + ele / 2 * phi)
 96         UHR = numpy.array(UHR)
 97         return UHR
 98 
 99 
100     def __calc_UHalfLeft(self, U):
101         Ui = U[1:-2]
102         UiMinusOne = U[0:-3]
103         UiPlusOne = U[2:-1]
104 
105         tmpItem = Ui - UiMinusOne
106         UHL = list()
107         for idx, ele in enumerate(tmpItem):
108             if ele == 0:
109                 UHL.append(Ui[idx])
110             else:
111                 r = (UiPlusOne[idx] - Ui[idx]) / ele
112                 phi = self.__get_limitor(r)
113                 UHL.append(Ui[idx] + ele / 2 * phi)
114         UHL = numpy.array(UHL)
115         return UHL
116 
117 
118     def __get_limitor(self, r):
119         phi = 0
120         if r >= 0:
121             phi = 2 * r / (1 + r)
122         return phi
123 
124 
125     def __fill_U_boundary(self, UOld):
126         tmpUOld = numpy.hstack(([0], UOld, [0]))
127         return tmpUOld
128 
129 
130     def __calc_U0(self):
131         '''
132         计算第0层时间步数值
133         '''
134         U0 = self.__calc_u0(self.__X)
135         return U0
136 
137 
138     def __calc_u0(self, x):
139         u0 = numpy.sin(2 * numpy.pi * x)
140         return u0
141 
142 
143     def __init_grid(self):
144         xMin, xMax = 0, 1
145         tMin, tMax = 0, 0.5
146         self.__hx = (xMax - xMin) / self.__nx
147         self.__ht = (tMax - tMin) / self.__nt
148         self.__X_interface = numpy.linspace(xMin, xMax, self.__nx + 1)
149         self.__X = (self.__X_interface[:-1] + self.__X_interface[1:]) / 2
150         self.__T = numpy.linspace(tMin, tMax, self.__nt + 1)
151 
152 
153 class BurgersPlot(object):
154 
155     fig = None
156     ax1 = None
157     line = None
158     txt = None
159     T, X, UList = None, None, None
160 
161     @classmethod
162     def plot_ani(cls, burgersObj):
163         cls.fig = plt.figure(figsize=(6, 4))
164         cls.ax1 = plt.subplot()
165         cls.line = cls.ax1.plot([], [], lw=3)[0]
166         cls.txt = cls.ax1.text(x=0.8, y=0.8, s="t = {:.3f}".format(0))
167         cls.T, cls.X, cls.UList = burgersObj.get_solu()
168 
169         ani = animation.FuncAnimation(cls.fig, cls.update, frames=numpy.arange(len(cls.UList)), init_func=cls.init, blit=True, interval=50, repeat=True)
170         ani.save("plot_ani.gif", writer="PillowWriter", fps=20)
171         
172         plt.close()
173 
174 
175     @classmethod
176     def update(cls, frame):
177         cls.line.set_data(cls.X, cls.UList[frame])
178         cls.txt.set_text("t = {:.3f}".format(cls.T[frame]))
179         return cls.line, cls.txt
180 
181 
182     @classmethod
183     def init(cls):
184         cls.ax1.set(xlim=(0, 1), ylim=(-1, 1), xlabel="x", ylabel="u")
185         return cls.line, cls.txt
186 
187 
188     @staticmethod
189     def plot_fig(burgersObj):
190         T, X, UList = burgersObj.get_solu()
191 
192         fig = plt.figure(figsize=(6, 4))
193         ax1 = plt.subplot()
194         for U in UList:
195             ax1.plot(X, U)
196         ax1.set(xlabel="x", ylabel="u")
197 
198         fig.savefig("plot_fig.png", dpi=100)
199         # plt.show()
200         plt.close()
201 
202 
203 
204 if __name__ == "__main__":
205     burgersObj = BurgersEq(200, 100)
206     BurgersPlot.plot_ani(burgersObj)
207     # BurgersPlot.plot_fig(burgersObj)
    View Code
  • 结果展示:
  • 使用建议:
    ①. 此gif的保存需要安装pillow库(cmd下: pip install pillow);
    ②. 限制器函数$\phi (r)$在$r > 1$情形下的取值范围通过$0 < r < 1$的对称性给出. 笔者能力所限, 理解不太透彻, 读者不吝批评指正.
  • 参考文档:
    Numerical Methods for PDE 2016 by Professor Qiqi Wang & Jacob White from MIT
posted @ 2020-10-09 22:45  LOGAN_XIONG  阅读(851)  评论(0)    收藏  举报