4-8 数值稳定性和模型初始化

4-8 数值稳定性和模型初始化

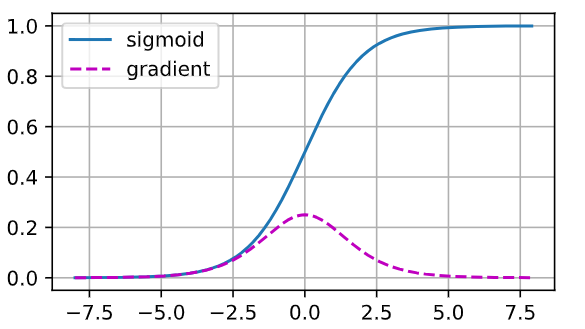
当sigmoid函数的输入很大或是很小时，它的梯度都会消失。

此外，当反向传播通过许多层时，除非我们在刚刚好的地方，这些地方sigmoid函数的输入接近于零，否则整个乘积的梯度可能会消失。

当我们的网络有很多层时，除非我们很小心，否则在某一层可能会切断梯度。事实上，这个问题曾经困扰着深度网络的训练。因此，更稳定的ReLU系列函数已经成为从业者的默认选择（虽然在神经科学的角度看起来不太合理）。

1. %matplotlib inline
   这是 Jupyter Notebook 的魔法命令，让接下来的绘图直接在 notebook 里显示出来，而不是弹出一个新窗口。
2. import torch
   导入 PyTorch 主库。
3. from d2l import torch as d2l
   从 d2l（Dive-into-Deep-Learning 配套工具包）里导入针对 PyTorch 封装的绘图与工具函数，起别名 d2l，下面用 d2l.plot 直接画图。
4. x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
   生成一维张量 x，取值范围 [-8, 8)，步长 0.1，共 160 个数；requires_grad=True 表示后续要对这个张量求梯度。
5. y = torch.sigmoid(x)
   对 x 逐元素计算 Sigmoid 函数：
   σ(x) = 1 / (1 + e^(−x))，结果保存在 y 中。
6. y.backward(torch.ones_like(x))
   反向传播。torch.ones_like(x) 产生和 x 同形状的“全 1”张量，作为外部梯度（因为 y 是向量而非标量，PyTorch 需要指定对 y 各分量求导时的权重）。
   执行后，x.grad 里保存了 ∂y/∂x，即 Sigmoid 的导数 σ′(x)=σ(x)(1−σ(x))。
7. d2l.plot(...)
   用 d2l 封装的绘图函数一次性画两条曲线：
   • x.detach().numpy()：把 x 从计算图中分离并转成 NumPy 数组，作为横坐标；
   • [y.detach().numpy(), x.grad.numpy()]：两条纵坐标曲线，分别是 Sigmoid 值和对应梯度；
   • legend 设置图例；
   • figsize 设定图像大小（4.5×2.5 英寸）。

%matplotlib inline  # 在 Jupyter 中内嵌显示图像
import torch
from d2l import torch as d2l

# 生成从 -8 到 8（不含 8），步长 0.1 的张量，并开启梯度追踪
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)

# 对 x 逐元素计算 Sigmoid 函数
y = torch.sigmoid(x)

# 反向传播：对 y 关于 x 求梯度，外部梯度设为全 1
y.backward(torch.ones_like(x))

# 绘制 Sigmoid 曲线及其梯度曲线
d2l.plot(x.detach().numpy(),   # 横坐标：x 值
         [y.detach().numpy(),   # 纵坐标 1：Sigmoid 输出
          x.grad.numpy()],  # 纵坐标 2：对应梯度
         legend = ['sigmoid', 'gradient'],   # 图例
         figsize=(4.5, 2.5))  # 图像大小

1.梯度爆炸

# 从标准正态分布 N(0,1) 中采样，生成一个形状为 4×4 的随机矩阵 M
M = torch.normal(0, 1, size=(4, 4))
print('一个矩阵\n', M)
for i in range(100):
    # 每次循环都：
    # 1) 再生成一个新的 4×4 随机矩阵（同样服从 N(0,1)）
    # 2) 用 torch.mm 做矩阵乘法，把结果写回 M
    #    等价于 M = M @ torch.normal(0, 1, size=(4, 4))
    M = torch.mm(M, torch.normal(0, 1, size=(4, 4)))

print('乘以100个矩阵后\n', M)

一个矩阵
 tensor([[-0.3257, -1.9629,  1.7383,  1.9050],
        [ 1.1481,  0.7473,  0.2440,  2.6464],
        [ 0.0243,  0.6882,  0.0065,  0.6089],
        [-0.0987,  0.1785, -1.2354, -0.6053]])
乘以100个矩阵后
 tensor([[-2.3577e+22, -4.7567e+22, -2.0264e+22, -2.0735e+22],
        [-1.2601e+22, -2.5423e+22, -1.0830e+22, -1.1082e+22],
        [-2.6170e+21, -5.2797e+21, -2.2492e+21, -2.3015e+21],
        [ 1.0494e+22,  2.1172e+22,  9.0197e+21,  9.2295e+21]])