CTAug——Graph Contrastive Learning with Cohesive Subgraph Awareness | 具有衔接子图意识的图对比学习。

论文信息

论文标题：Graph Contrastive Learning with Cohesive Subgraph Awareness
论文作者：吴雨澄、王乐野、韩笑、叶瀚嘉
论文来源：
发布时间：2024-02-21
论文地址：link
论文代码：link

1 Introduction

1.1 研究背景：图对比学习（GCL）的定位与核心逻辑

• GCL 的作用：作为一种有前景的自监督学习范式，用于学习图和节点嵌入，支撑社交网络分析、Web 图挖掘等多种应用场景 [28, 47, 58, 60]。

• 核心思想：通过最大化同一原始图生成的不同增强视图之间的表示一致性 [54]，训练出高效的图神经网络（GNN）编码器。

• 增强策略的重要性：视图生成的增强策略是 GCL 的关键环节，分为拓扑增强和特征增强两类 [58]，本文聚焦拓扑增强—— 因其可同时应用于带属性图和无属性图，适用范围更广。

1.2 现有拓扑增强方法的现状与局限

1.2.1 主流增强方式与特点

增强类型	具体操作	典型方法 / 逻辑	存在问题
概率型增强	节点删除、边移除、子图采样等 [58]	1. 纯随机操作：以同等概率删除节点 / 边（如 GraphCL [54, 59]）；   2. 基于重要性的调整：认为应保留图中更重要的组件，避免随机删除重要元素导致增强视图偏离原始图 [相关研究]	1. 纯随机操作未考虑节点 / 边的重要性差异；   2. 现有基于重要性的方法仍存在改进空间
确定性增强	基于扩散的操作（如个性化 PageRank [17]、马尔可夫链 [57]）	MVGRL [17]：通过确定性、解析性的扩散过程为原始图生成单一固定的增强视图 [17, 58]	未充分利用图的内在结构属性，增强逻辑相对单一

1.2.2 现有研究的突破与不足

• 部分突破：近年已有研究开始利用图的内在属性或领域知识指导 GCL 的拓扑增强，例如 GCA [60] 引入边中心性，优先保留重要边 [41, 45, 56, 60]。

• 核心不足：上述研究仍未解决三大关键问题，构成本文的研究动机。

1.3 本文的核心研究问题（三大待解决问题）

1.3.1 问题 1：属性丰富性（Property Enrichment）

• 现状：现有 GCL 增强仅利用了极少数类型的图属性（如中心性 [60]）来判断图组件的重要性，以优化增强效果。

• 矛盾：现实社交图中存在大量个体级（节点 / 边）和结构级的内在属性 [18, 46]，这些属性已被证明可提升多种图应用的性能，但尚未被充分整合到 GCL 的拓扑增强中。

• 核心疑问：能否通过引入更多关键图属性，丰富拓扑增强的依据，进而提升 GCL 性能？

1.3.2 问题 2：统一框架（Unified Framework）

• 现状：现有研究多聚焦于设计特定的 GCL 机制以实现表示学习，而拓扑增强是各类 GCL 机制中广泛采用的步骤 [58]。

• 矛盾：缺乏一个统一框架，将图属性灵活整合到所有主流 GCL 机制中，导致属性的复用性和 GCL 的通用性受限。

• 核心疑问：能否构建统一框架，让图属性为不同 GCL 机制的拓扑增强提供支持，进而普遍提升图表示学习效果？

1.3.3 问题 3：表达性网络（Expressive Network）

• 现状：多数 GCL 方法 [17, 54] 采用 GCN [21]、GIN [50] 等标准 GNN 作为编码器。

• 矛盾：已有研究证明 [11]，标准 GNN 的表达能力有限，难以有效捕捉子图属性（如子图结构特征），制约了 GCL 对图深层结构信息的利用。

• 核心疑问：能否设计更具表达性的图编码器，使其能从原始图中有效提取子图信息？

1.4 本文的核心思路与贡献预告

1.4.1 核心解决思路

1. 引入凝聚子图（Cohesive Subgraphs）：将凝聚子图（图中紧密连接的重要节点子集，如 k-clique [30]、k-core [6, 36]、k-truss [12]）作为新的结构级属性，指导拓扑增强 —— 核心是在增强视图中保留原始图的凝聚子图，弥补现有属性（如中心性）的不足 [14, 20, 24]。

2. 构建统一框架 CTAug：针对概率型和确定性两类拓扑增强，分别设计适配策略，让凝聚子图感知能灵活融入各类 GCL 机制；同时扩展至节点级表示学习 [60]。

3. 优化编码器：O-GSN：提出面向原始图的子图网络（O-GSN），增强 GNN 捕捉凝聚子图属性的能力，解决标准 GNN 表达性不足的问题 [9, 11]。

1.4.2 核心贡献预告（全文总结性贡献）

1. 开创性整合：首次将凝聚属性融入 GCL，为自监督图学习范式中整合图内在知识提供了新思路（将凝聚性视为图的内在知识 [60]）。

2. 统一框架 CTAug：提出可在拓扑增强和图学习过程中考虑多种凝聚属性的统一框架，从理论上证明其优于传统 GCL 方法。

3. 实验验证：在真实数据集上验证 CTAug 能显著提升 GraphCL [54]、JOAO [53]、MVGRL [17]、GCA [60] 等现有 GCL 机制的性能，尤其对高平均度图效果突出。

2 Method

  

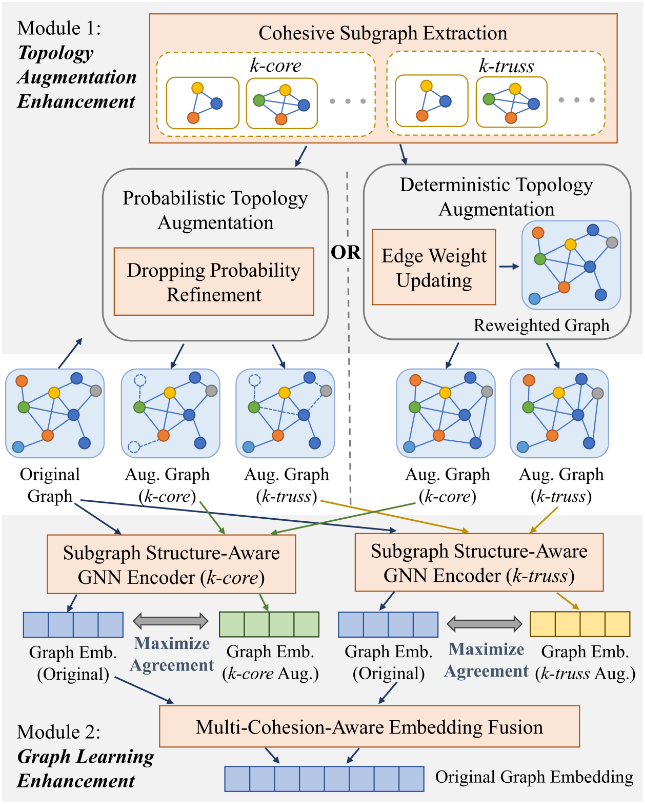
2.1 框架核心背景：GCL 基础逻辑与 CTAug 设计目标

2.1.1 GCL 的核心目标与损失函数

• 目标：通过最大化相似图对的表示一致性、最小化不相似图对的表示一致性，学习高质量图表示。

• 基础损失函数：针对图对 $G_1$ （表示 $z_1$ ）和 $G_2$ （表示 $z_2$ ），损失函数定义为：

    $L=-log \frac{exp \left(sim\left(z_{1}, z_{2}\right) / \tau\right)}{\sum_{i, j} exp \left(sim\left(z_{i}, z_{j}\right) / \tau\right)}$

    其中， $\tau$ 为温度参数， $sim(z_i,z_j)=z_i^T z_j /(\|z_i\|\|z_j\|)$ 表示余弦相似度。

• • 相似图对（如同一原始图生成的增强图）： $z_1$ 与 $z_2$ 应相近，分子增大，损失减小；

• • 不相似图对（如不同原始图生成的增强图）：分母增大，损失增大；

2.1.2 CTAUG 的核心设计目标

• 针对概率型拓扑增强（如随机节点 / 边删除 [54]），解决其可能破坏原始图凝聚组件（“连接性强的子结构”）的问题，确保增强图尽可能保留原始图的凝聚子图结构。

• 框架整体定位：通过两大核心模块，在 GCL 的拓扑增强和图学习环节均融入凝聚子图感知，全程突出图的凝聚属性。

  • 模块 1：改进增强过程，生成能保留原始图 “内聚性” 的增强图；

  • 模块 2：优化图神经网络（GNN）编码器，使其生成的图表示能更好捕捉原始图的 “内聚性”

2.2 模块 1：拓扑增强增强（Topology Augmentation Enhancement）

2.2.1 概率型拓扑增强优化（Probabilistic Topology Augmentation）

1️⃣ 优化思路与核心问题

• 传统问题：传统图增强方法，先生成多个候选增强图，再选与原始图特定凝聚性最相似的图，但该过程因需生成多图并计算凝聚子图而耗时。

• 优化方案：通过调整增强操作概率，让凝聚子图中的节点和边更易保留在增强图中，仅需生成 1 个增强图即可大概率维持原始图的特定凝聚性 —— 核心是降低凝聚子图内节点 / 边的删除概率。

2️⃣ 具体概率调整方法

1. 基础概率衰减：对原始图凝聚子图上的 节点 / 边 删除概率 $p_{dr}$，乘以衰减因子 $\epsilon \in(0,1]$ ，得到调整后的删除概率：

     $p_{dr}'=(1-\epsilon) \cdot p_{dr}$

• 示例：若原始节点删除概率 $p_{dr}=0.2$ ，设 $\epsilon=0.5$ ，则凝聚子图内节点的删除概率降至 $0.2×0.5=0.1$ 。

2. 基于节点重要性的动态概率调整：考虑不同 $k$ 值下的凝聚子图（如 $\text{k-core}$），量化节点重要性并动态调整删除概率：

• • 步骤 1：提取多 $k$ 值凝聚子图集合：对原始图 $G$ ，$k$ 从 $k_{min}$ 到 $k_{max}$，得到子图集合：

      $\mathbb{S}=\{S_{core}^k | k=k_{min},k_{min}+1,...,k_{max}\}$ ；

• • 步骤 2：计算节点重要性权重 $w_v$ ：对节点 $v_i$ ，统计其在 $\mathbb{S}$ 中出现的次数： 

      $w_v(v_i)=\sum_{S \in \mathbb{S}} 1_{v_i \in vertex(S)}$

• • 步骤 3：权重归一化

      $w_v'(v_i)=\frac{w_v(v_i)}{max\ w_v} \in[0,1]$

      确保权重在 [0,1] 区间；

• • 步骤 4：动态调整删除概率

      $p_{dr}'(v_i)=(1-w_v'(v_i)·\epsilon)·p_{dr}$

      一般形式：$p_{dr}'(v_i)=(1-f(w_v'(v_i))·\epsilon)·p_{dr}$ （ $f$ 为 [0,1] 输入输出的单调递增函数）。

3. 边删除概率调整：边的删除概率取其两端节点调整后删除概率的平均值：

    $p_{dr}'(e_{ij})=(p_{dr}'(v_i)+p_{dr}'(v_j))/2$ 

2.2.2 确定型拓扑增强优化（Deterministic Topology Augmentation）

1️⃣ 传统确定型增强的特点

• 代表方法：MVGRL [17]，基于个性化 PageRank [32] 扩散过程生成单一固定增强图，扩散过程可通过闭形式计算：

     $S=\alpha\left(I-(1-\alpha) D^{1/2} A D^{-1/2}\right)^{-1}$

• 核心问题：扩散过程未考虑凝聚子图属性，可能弱化重要凝聚结构。

2️⃣ CTAug 的优化策略：凝聚感知的权重调整

• 核心思路：对凝聚子图内的边赋予更大权重，使扩散过程更倾向于保留这些边 —— 通过调整邻接矩阵中边的权重实现。

• 具体步骤（以 k-core 为例）：

1. 提取多 k 值 k-core 子图集合 $\mathbb{S}=\{S_{core}^k | k=1,2,...,k_{max}\}$ ；

2. 计算节点重要性权重 $w_v$ ：同概率型增强步骤 2，统计节点在 $\mathbb{S}$ 中出现次数；

3. 节点权重归一化（含平衡因子）：

       $\begin{aligned} & w_v'(v_i)=\eta·\frac{w_v(v_i)}{\overline{w}_v}+(1-\eta)·1 \\ & \overline{w}_v=\frac{\sum_{v_i \in vertex(G)} w_v(v_i)}{|vertex(G)|} \end{aligned}$

      其中， $\eta \in[0,1]$ 为凝聚属性影响因子， $\eta$ 越接近 1，凝聚属性的考虑程度越高；

4. 调整边权重：设原始边权重为 $w_e(e_{ij})$ ，调整后权重 $w_e'(e_{ij})=\frac{1}{2}(w_v'(v_i)+w_v'(v_j))w_e(e_{ij})$ ；

5. 凝聚感知扩散：用调整后的邻接矩阵 $A'$ （ $A'_{i,j}=w_e'(e_{ij})$ ）替换原始 $A$ ，代入扩散公式计算，生成增强图。

2.3 模块 2：图学习增强（Graph Learning Enhancement）

2.3.1 子图感知 GNN 编码器（Subgraph-aware GNN Encoder）：O-GSN

1️⃣ 传统 GNN 的局限与 GSN 的启发

• 传统 GNN 问题：基于消息传递（MPNN）框架 [16,31,50]，但难以有效捕捉子图属性（如子结构计数 [11]），导致增强图中保留的凝聚子图信息在编码过程中丢失。

• GSN 的启发：GSN [9] 是一种拓扑感知图学习方案，通过在邻域聚合中引入子结构编码特征 $s_v$ ，增强 GNN 的子图感知能力，其聚合过程为：

     $GSN: AGG\left((h_v, h_u, s_v, s_u)_{u \in \mathcal{N}(v)}\right)$

    其中，

• • • $AGG$ 为聚合函数（如 $\sum_{u \in \mathcal{N}(v)} MLP(·)$ ），

    • $h_v$ 为节点 $v$ 的隐藏状态，

    • $s_v$ 为节点 $v$ 的子结构编码特征（如节点在不同子图中的出现次数）；

    通过拼接 $h_v$ 与 $s_v$ 得到更新后的隐藏状态 $h_v'=[h_v,s_v]$ ，再进行消息传递。

2️⃣ O-GSN 的设计：解决 GSN 的两大问题

• GSN 的问题：

1. 低效性：需为每个增强图在线计算子结构编码特征，耗时极高；

2. 原始图追踪丢失：不同原始图可能生成相同增强图，GSN 无法区分其来源。

• O-GSN 的优化：使用原始图的子结构编码特征，而非增强图的特征：

     $O-GSN: AGG\left((h_v, h_u, s_v^o, s_u^o)_{u \in \mathcal{N}(v)}\right)$

    其中， $s_v^o$ 为节点 $v$ 在原始图中的子结构编码特征。

• • 优势 1：效率提升 —— 仅需在数据预处理阶段计算原始图的子结构编码特征，无需在线重复计算；

• • 优势 2：保留原始图关联 —— 通过原始图特征，可区分相同增强图的不同原始图来源，提升编码器表达能力。

3️⃣ O-GSN 中的子结构选择

• 核心原则：选择能代表 k-core/k-truss 凝聚子图的子结构，本文聚焦团（clique）子结构。

2.3.2 多凝聚嵌入融合（Multi-Cohesion Embedding Fusion）

1️⃣ 融合动机

  不同凝聚属性（如 k-core 与 k-truss）可识别图中不同的重要部分，整合多凝聚属性的嵌入结果，可进一步提升表示质量。

2️⃣ 融合方法

• 步骤 1：针对每种凝聚属性 $c \in \mathbb{C}$ （ $\mathbb{C}$ 为凝聚属性集合，如 {k-core, k-truss}），分别通过 “拓扑增强优化 + O-GSN 编码” 训练 GNN 编码器，得到对应嵌入 $z_i^c \in \mathbb{R}^{n×d}$ （ $n$ 为节点数， $d$ 为嵌入维度）；

• 步骤 2：拼接多凝聚属性的嵌入，得到最终图嵌入： $z_i=\|_{c \in \mathbb{C}} z_i^c$，最终嵌入维度为 $n×(d·|\mathbb{C}|)$ 。

2.4 扩展：节点嵌入学习（Extension for Node Embedding Learning）

2.4.1 节点级 GCL 的特点

• 主流类型：局部 - 局部 GCL（Local-Local GCL），通过比较节点对学习节点嵌入 [58]，代表方法如 GRACE [59]、GCA [60]；

• 增强策略：为确保所有节点保留在增强图中，通常仅采用边删除操作 ——GRACE 用随机边删除，GCA 用基于中心性的自适应边删除。

2.4.2 CTAug 的扩展适配

• 适配逻辑：节点级 GCL 的边删除操作与图级 GCL 的边删除逻辑一致，因此可复用模块 1 中 “基于凝聚子图的边删除概率调整” 方法，增强 GRACE/GCA 的边删除策略；
• 注意事项：凝聚属性是图的子结构级属性，对节点嵌入的影响程度弱于对图嵌入的影响，因此提升效果相对温和。

3 EXPERIMENTS

3.1 实验基础：数据集与实验设置

3.1.1 数据集选择与统计

  实验选用 7 个真实数据集，涵盖社交图和生物医学图两大类，用于验证 CTAug 在图分类任务中的有效性；后续节点分类任务额外补充 3 个数据集。所有数据集统计信息如下表所示：

  

3.1.2 实验设置

• 任务类型：无监督图表示学习（GCL 标准基准设置 [58]），下游任务为图分类和节点分类。

• 评估方式：

• 图分类：基于学习到的图嵌入训练线性 SVM 分类器，采用 10 折交叉验证，重复实验 5 次，以准确率（Accuracy） 为评价指标 [54]；

• 节点分类：采用标准节点分类评估流程，对比增强前后方法的准确率。

• 硬件环境：28 核 Intel CPU、96GB RAM、Tesla V100S GPU，操作系统为 Ubuntu 18.04.5 LTS。

3.2 基线方法（Baselines）介绍

  实验选择9 种主流 GCL 方法作为图分类任务基线，覆盖概率型、确定型等不同增强类型；节点分类任务额外选择 2 种节点级 GCL 方法，具体如下：

方法类别	方法名称	核心特点	适用场景
概率型拓扑增强 GCL	GraphCL [54]	经典概率型 GCL，采用随机节点删除、边删除等纯随机增强操作，设置统一删除概率	图级表示学习
概率型拓扑增强 GCL	JOAO [53]	概率型 GCL，通过自动化策略优化增强视图生成，提升表示一致性	图级表示学习
概率型拓扑增强 GCL	AD-GCL [39]	基于对抗学习的 GCL，通过对抗性增强生成多样化视图，提升泛化能力	图级表示学习
概率型拓扑增强 GCL	AutoGCL [52]	自适应学习增强视图生成概率，无需人工调参，优化表示质量	图级表示学习
概率型拓扑增强 GCL	RGCL [25]	基于不变性原理的 GCL，通过挖掘图的不变特征指导增强，提升鲁棒性	图级表示学习
概率型拓扑增强 GCL	GCL-SPAN [26]	聚焦谱域信息的 GCL，通过最大化增强过程中的谱变化生成视图	图级表示学习
确定型拓扑增强 GCL	MVGRL [17]	经典确定型 GCL，基于个性化 PageRank 扩散过程生成单一固定增强视图	图级表示学习
非显式增强 GCL	SimGRACE [49]	无显式数据增强，通过扰动 GNN 编码器实现对比学习，避免增强带来的结构破坏	图级表示学习
互信息最大化 GCL	InfoGraph [38]	基于互信息最大化的 GCL，通过最大化图级与节点级表示的互信息学习嵌入	图级表示学习
节点级 GCL	GRACE [59]	局部 - 局部 GCL，采用随机边删除生成增强视图，通过节点对对比学习节点嵌入	节点级表示学习
节点级 GCL	GCA [60]	GRACE 的改进版，引入边中心性指导自适应边删除，提升节点嵌入质量	节点级表示学习
其他基线	DeepWalk+features [无]	基于随机游走的传统图表示方法，结合节点特征生成嵌入	节点级表示学习
其他基线	GAE/VGAE [无]	基于自编码器的图表示方法，通过重构邻接矩阵学习嵌入	节点级表示学习
其他基线	DGI [无]	基于深度图信息最大化的方法，通过对比局部与全局表示学习嵌入	节点级表示学习

  CTAug 增强方法定义

  为验证 CTAug 的通用性，将其应用于 3 种代表性 GCL 方法，形成增强方法：

• • CTAug-GraphCL：CTAug 增强 GraphCL（概率型）；

• • CTAug-JOAO：CTAug 增强 JOAO（概率型）；

• • CTAug-MVGRL：CTAug 增强 MVGRL（确定型）；

• • CTAug-GRACE/CTAug-GCA：CTAug 增强 GRACE/GCA（节点级）。

  凝聚属性选择：k-core 和 k-truss（通过 NetworkX 工具包 [6,12] 的算法提取）。

3.3 实验内容、结果与结论

  实验分为图分类实验、节点分类实验、消融实验、可扩展性实验四大类，分别验证 CTAug 的有效性、适用场景及模块贡献。

3.3.1 实验 1：图分类实验（核心实验）

1️⃣ 实验内容

• 目标：验证 CTAug 对不同类型 GCL 方法（概率型、确定型）的增强效果，重点分析在高 / 低平均度图上的性能差异；

• 变量：数据集（高平均度：IMDB-B、IMDB-M、COLLAB；低平均度：RDT-B、RDT-T、ENZYMES、PROTEINS）、GCL 方法（基线 vs CTAug 增强版）；

• 指标：10 折交叉验证后的准确率（均值 ± 标准差）。

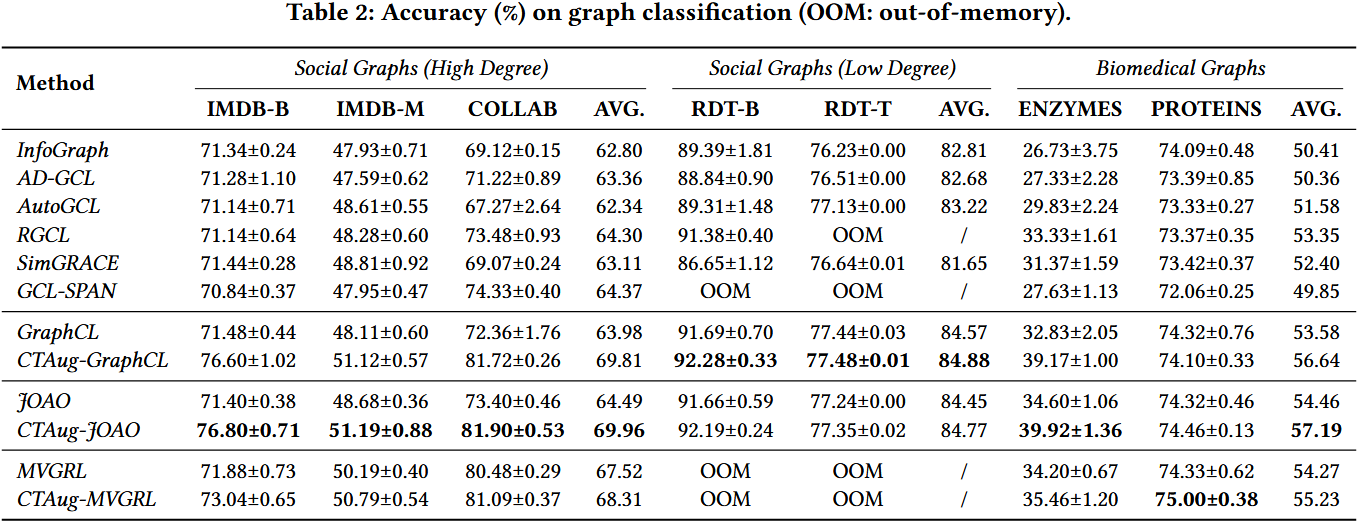
2️⃣ 实验结果

  

3️⃣ 关键结论

1. CTAug 对概率型 GCL 增强效果显著：

• 高平均度社交图上，CTAug-GraphCL 较 GraphCL 平均提升 5.83%，CTAug-JOAO 较 JOAO 平均提升 5.47%；其中 COLLAB 数据集（平均度数最高，~65）提升最显著，CTAug-GraphCL 提升 9.36%，CTAug-JOAO 提升 8.5%—— 验证了 “高平均度图含更多高凝聚子图，CTAug 更能发挥作用” 的假设。

• 低平均度社交图（RDT-B/T，平均度数～2）上，CTAug 提升微弱（<0.5%）—— 原因是低平均度图缺乏明显的高凝聚子图，CTAug 的凝聚感知优势无法体现。

2. CTAug 对确定型 GCL 增强效果温和：

• CTAug-MVGRL 较 MVGRL 在高平均度图上平均提升 0.79%，提升幅度远低于概率型 —— 原因是 MVGRL 已将节点度数作为隐含特征（高度数节点常属于高凝聚子图），与 CTAug 的凝聚感知存在部分重叠，补充增益有限。

• MVGRL 在 RDT-B/T 等大型低平均度图上因内存不足（OOM）无法运行，而 CTAug-GraphCL/JOAO 可正常运行，说明概率型增强 + CTAug 的组合更具实用性。

3. 生物医学图上的表现：

• CTAug 在生物医学图（平均度数～3）上有一定提升（CTAug-GraphCL 平均提升 3.06%），但低于高平均度社交图 —— 原因是生物医学图的凝聚子图密度低于高平均度社交图，凝聚属性对任务的贡献有限。

3.3.2 实验 2：节点分类实验

1️⃣ 实验内容

• 目标：验证 CTAug 在节点级 GCL 任务中的有效性；

• 数据集：Coauthor-CS、Coauthor-Physics、Amazon-Computers（平均度数：Amazon-Computers~35，其余～10）；

• 方法：对比 GRACE/GCA（基线）与 CTAug-GRACE/CTAug-GCA（增强版）的准确率。

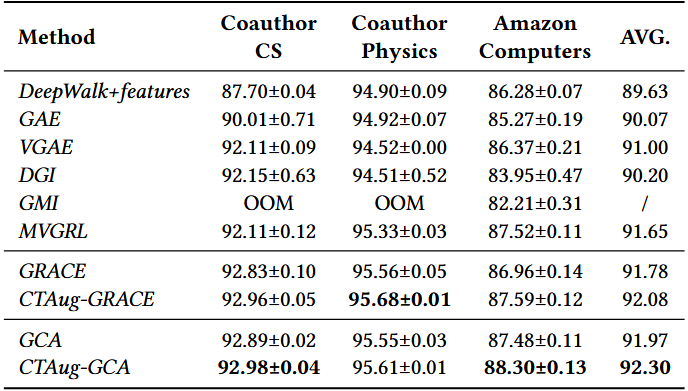
2️⃣ 实验结果

  

 

3️⃣ 关键结论

1. CTAug 对节点级 GCL 有小幅提升：CTAug-GRACE 平均提升 0.3%，CTAug-GCA 平均提升 0.33%—— 原因是凝聚属性是子结构级属性，对全局图嵌入的影响大于对单个节点嵌入的影响，因此节点分类任务的提升幅度低于图分类。

2. 高平均度图上提升更明显：Amazon-Computers（平均度数～35）上，CTAug-GCA 提升 0.82%，高于其他两个低平均度数据集（提升～0.1%）—— 再次验证 “CTAug 在高凝聚子图丰富的高平均度图上效果更优”。

3.3.3 实验 3：消融实验（模块有效性验证）

1️⃣ 实验内容

• 目标：验证 CTAug 两大核心模块（模块 1：拓扑增强增强；模块 2：图学习增强（O-GSN））的单独作用及组合效果；

• 数据集：高平均度社交图（IMDB-B、IMDB-M、COLLAB）；

• 方法：对比 CTAug-GraphCL（全模块）、仅模块 1、仅模块 2、仅 k-core、仅 k-truss 的准确率。

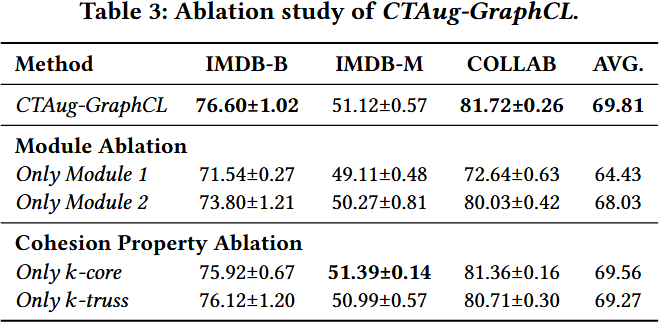
2️⃣ 实验结果

  

方法	IMDB-B	IMDB-M	COLLAB	平均
CTAug-GraphCL（全模块）	76.60±1.02	51.12±0.57	81.72±0.26	69.81
仅模块 1（拓扑增强）	71.54±0.27	49.11±0.48	72.64±0.63	64.43
仅模块 2（O-GSN）	73.80±1.21	50.27±0.81	80.03±0.42	68.03
仅 k-core（单凝聚属性）	75.92±0.67	51.39±0.14	81.36±0.16	69.56
仅 k-truss（单凝聚属性）	76.12±1.20	50.99±0.57	80.71±0.30	69.27

4️⃣ 关键结论

1. 两大模块缺一不可：仅模块 1 或仅模块 2 的准确率均低于全模块（仅模块 1 低 5.38%，仅模块 2 低 1.78%），证明模块 1（保留凝聚子图）与模块 2（捕捉凝聚子图信息）存在协同作用 —— 模块 1 为模块 2 提供高质量增强图，模块 2 解决传统 GNN 无法有效编码子图信息的问题。

2. 模块 2（O-GSN）贡献更大：仅模块 2 的平均准确率（68.03%）远高于仅模块 1（64.43%）—— 原因是传统 GNN（如 GraphCL 默认的 GIN）无法有效捕捉子图属性 [11]，即使模块 1 保留了凝聚子图，编码器仍会丢失信息；而 O-GSN 可弥补这一缺陷，因此贡献更显著。

3. 多凝聚属性融合增益有限：仅 k-core 与仅 k-truss 的准确率接近（69.56% vs 69.27%），且与全模块（69.81%）差距小 —— 原因是 IMDB-B/M 中 k-core 与 k-truss 子图的节点 / 边重叠率超 95%，属性冗余度高，融合未带来明显额外收益。

3.3.4 实验 4：可扩展性实验（效率验证）

  

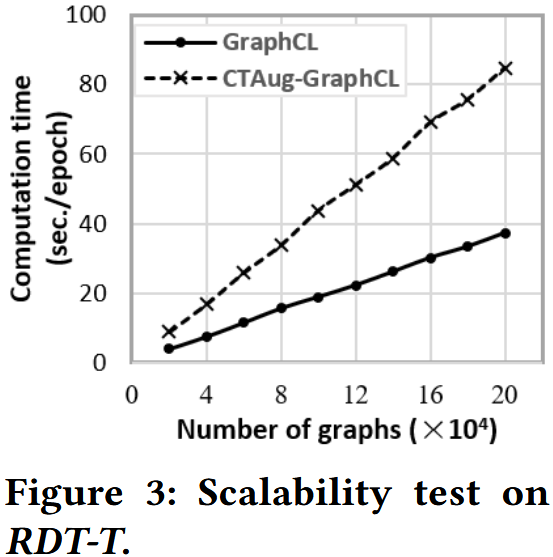
1️⃣ 实验内容

• 目标：验证 CTAug 的训练效率及预处理耗时；

• 指标：训练时间（随训练图数量变化）、预处理耗时（凝聚子图提取 + O-GSN 特征计算）。

2️⃣ 实验结果

1. 训练时间：

• 如图 3 所示，CTAug-GraphCL 的训练时间约为 GraphCL 的 2 倍 —— 原因是 CTAug 需同时处理 k-core 和 k-truss 两种凝聚属性的嵌入；若仅使用一种凝聚属性，训练时间开销可大幅降低（接近 GraphCL）。

2. 预处理耗时：

• 单图的 k-core/k-truss 提取耗时约 $10^{-2}$ 秒（多项式时间算法 [6,43]）；

• O-GSN 的子结构编码特征计算耗时最多几秒（预处理阶段离线完成）；

• 预处理支持并行化，可批量处理数据集，不影响训练阶段效率。

3️⃣ 关键结论

  CTAug 虽引入一定时间开销，但预处理可离线 / 并行化，且单凝聚属性场景下效率接近基线方法，具备实际应用可行性。