ENGAGE: Explanation Guided Data Augmentation for Graph Representation Learning | ENGAGE:用于图表示学习的解释引导数据增强
论文信息
论文标题:Explanation-Preserving Augmentation for Semi-Supervised Graph Representation Learning
论文作者:史玉成, 周凯雄, 刘宁浩
论文来源:ECML-PKDD 2023
发布时间:2023-07-03
论文地址:link
论文代码:link
1 Introduction
1.1 研究背景:图表示学习的重要性与现状
- 图表示学习的价值:在众多图分析任务中(如节点分类、图分类等)展现出强大能力,可将图数据转化为低维、有意义的向量表示,为后续任务提供基础。其中,无监督图表示学习方法因在标签稀缺场景下的适应性,受到广泛关注。
- 对比学习的崛起:近年来,对比学习在无监督图表示学习中取得优异性能。其核心逻辑是通过从对比视图中学习表示,减少数据中的冗余信息,从而提升表示的有效性。
1.2 现有方法的核心问题
|
问题类别 |
具体表现 |
相关说明 |
|
随机扰动的局限性 |
多数现有工作(如 [2,3,57,52])采用随机采样进行数据增强,可能意外破坏图结构,导致表示的有效性降低 |
图结构包含节点间的关联信息,是图数据的核心特征,结构破坏会丢失关键信息,影响下游任务性能 |
|
跨领域方法迁移困难 |
在计算机视觉、自然语言处理等领域,已有利用语义信息 [22,35] 或领域知识 [4] 设计的智能数据增强方法,但难以迁移到图领域 |
图数据具有抽象性,难以定义和提取有意义的元素;且图的非欧几里得特性进一步增加了数据增强的难度 |
|
现有解决方案的缺陷 |
1. 依赖外部信息:如 Fang 等人 [5] 利用知识图谱增强原始输入图,仅适用于计算化学等特定领域,缺乏通用性
2. 指标不普适:如 Zhu 等人 [58] 用节点中心性作为节点重要性指标,但中心性是静态度量,并非在所有场景下都与下游任务相关
3. 计算成本高或黑箱特性:部分工作 [11,51] 设计端到端框架自动制定数据增强策略,但计算成本高,且黑箱特性无法明确定位图数据中的任务相关信息 |
这些缺陷导致现有方法难以在通用性、有效性和可解释性之间取得平衡,无法满足广泛的图表示学习需求 |
1.3 本文核心贡献:ENGAGE 框架的提出
- 框架设计:提出 ENGAGE(Explanation Guided Data Augmentation)框架,利用解释引导对比视图的生成,实现无监督图表示学习,在保留图关键部分的同时去除冗余信息。
- 解释方法创新:设计高效的无监督解释方法 ——Smoothed Activation Map(SAM),基于 latent 空间中表示的分布来衡量节点重要性,无需依赖监督信号,适用于多种图神经网络模型。
- 数据增强策略:结合 SAM 计算的节点重要性得分,设计针对图结构(边)和节点特征的两种数据增强方案,用于构建对比学习所需的成对图视图,避免随机扰动对图关键结构的破坏。
- 效率与适用性:SAM 方法借助量化技术 [14] 实现高效计算,可融入训练过程;ENGAGE 框架适用于节点级和图级多种任务,且能与不同模型架构兼容,灵活性高。
2 Method
2.1 减少表示中的冗余信息(Mitigating Superfluous Information in Representations)
核心目标
明确学习有效且鲁棒表示的核心准则 —— 最小化冗余信息,同时保留任务相关信息,为后续 ENGAGE 框架的设计提供理论导向。
关键定义与公式
- 充分表示(Sufficiency)
- 定义:若表示 $z$ 满足 $I(X; y) = I(z; y)$ ,则称 $z$ 对于标签 $y$ 是充分的。其中 $X$ 为原始输入, $y$ 为下游任务标签, $I(\cdot;\cdot)$ 表示互信息。
- 含义:充分表示需完整保留原始输入中与任务标签相关的信息,无信息丢失,是保证下游任务性能的基础(如图 3 (a) 所示, $z$ 包含 $X$ 中所有与 $y$ 相关的信息)。
- 互信息分解公式
- 公式: $I(X; z) = \underbrace{I(X; z| y)}_{superfluous information} + \underbrace{I(z; y)}_{task-relevant information}$
- 解读:
- 第一项 $I(X; z| y)$ :表示 $z$ 中包含的与预测 $y$ 无关的信息,即冗余信息,需最小化以提升表示的鲁棒性。
- 第二项 $I(z; y)$ :表示 $z$ 中对预测 $y$ 有用的信息,即任务相关信息,只要 $z$ 是充分表示,该项不受表示过程影响,需完整保留。
对比学习与解释的结合逻辑
- 对比学习的局限性:现有对比学习虽能控制表示中保留的信息量,但在无标签场景下,难以明确应保留输入中的哪些信息,易保留冗余内容。
- 解决方案:引入解释机制,通过解释识别图中的关键结构信息,在对比学习的数据增强过程中,优先保留这些关键信息,同时更大概率丢弃冗余信息,弥补对比学习的不足。
2.2 无监督表示的高效解释方法(Efficient Explanations for Unsupervised Representations)
1. 现有解释方法的痛点:Class Activation Map(CAM)的局限性
- 适用范围窄:CAM 专为特定模型架构(含 GCN 和全连接输出层)设计,无法适配多种图神经网络模型。
- 依赖监督信号:CAM 用于有监督模型,需利用输出层对应类别 $c$ 的权重 $w_{k}^{c}$ 计算节点重要性,无法直接应用于无监督图表示学习场景。
2. 核心创新:Smoothed Activation Map(SAM)
1)设计理念
2)GNN 前向传播过程基础
- 公式: $a_{i}^{l} = AGGREGATION^{l}\left(\left\{ F_{i^{\prime}}^{(l-1)}: n^{\prime} \in \mathcal{N}_{i}\right\}\right)$ , $F_{i}^{l} = COMBINE^{l}\left(F_{i}^{(l-1)}, a_{i}^{l}\right)$
- 符号含义: $F_{i}^{l}$ 为节点 $v_{i}$ 在第 $l$ 层的嵌入, $\mathcal{N}_{i}$ 为节点 $v_{i}$ 的邻居集合, $AGGREGATION^{l}$ 为第 $l$ 层的聚合函数, $COMBINE^{l}$ 为第 $l$ 层的组合函数。
3)SAM 计算逻辑
- 节点重要性得分公式: $\psi_{i} = ReLU\left( \sum_{k} \overline{w}_{k}F_{k,i}^{L}\right)$
- 符号含义: $\psi_{i}$ 为节点 $v_{i}$ 的重要性得分, $\overline{w}_{k}$ 为第 $k$ 个通道的平滑重要性得分, $F_{k,i}^{L}$ 为节点 $v_{i}$ 在最后一层( $L$ 层)第 $k$ 个 latent 维度的嵌入, $ReLU$ 函数用于过滤负重要性值。
- 通道平滑重要性得分 $\overline{w}_{k}$ 的计算
- 图级任务: $\overline{w}_{k}^{graph} = Norm\left( \sum_{n' \in \tilde{N}_{n}} Pool\left\{ F_{i'}^{L}: i' \in G_{n'}\right\}\right)[k]$
- 步骤:先对目标图 $G_{n}$ 在嵌入空间的邻居图集合 $\tilde{N}_{n}$ 中的每个图,通过 Pool(实验中用平均池化)操作从节点嵌入得到图级嵌入;再对这些图级嵌入求和,经 $L_2$ 归一化(Norm)后,取第 $k$ 个通道的值作为 $\overline{w}_{k}^{graph}$ 。
- 邻居图集合 $\tilde{N}_{n}$ :通过量化技术 [14] 高效获取,降低计算成本。
- 节点级任务: $\overline{w}_{k}^{node (i)} = Norm\left( \sum_{i' \in \tilde{N}_{i}} F_{i'}^{L}\right)[k]$
- 步骤:对目标节点 $v_{i}$ 在嵌入空间的邻居节点集合 $\tilde{N}_{i}$ 的最后一层嵌入求和,经 $L_2$ 归一化后,取第 $k$ 个通道的值作为 $\overline{w}_{k}^{node (i)}$ 。
4)SAM 的优势
- 通用性:适用于多种 GNN 模型,无需监督信号,适配无监督学习场景。
- 可靠性:通过局部平滑(整合邻近图 / 节点信息),降低单一图 / 节点解释的噪声,提升解释结果的可靠性。
- 高效性:基于 GNN 前向传播过程直接计算,无需额外的扰动输入或训练全局解释器,计算成本低,可融入训练过程。
5)SAM 算法流程(图级任务)
-
Step1:
- 操作内容:输入编码器 $f(\cdot)$ 和目标图 $G_{n} = \{V, E, A, X\} \in G$ ,计算图的节点嵌入 $Z = f(X, A)$ ,再通过 Pool 操作得到图级嵌入 $z$
- 目的:获取图的基础嵌入表示
-
Step2:
-
操作内容:在 latent 空间中找到目标图 $G_{n}$ 的 $m$ 个近邻图 $\tilde{N}_{n}$
-
目的:为局部平滑提供邻近图信息
-
-
Step3:
-
操作内容:计算平滑通道重要性得分 $\tilde{w}_{k}^{graph} = Norm(z + \sum_{n' \in \tilde{N}_{n}} z_{n'})[k]$
-
目的:整合目标图与近邻图信息,得到可靠的通道权重
-
-
Step4:
-
操作内容:遍历目标图 $G_{n}$ 的每个节点 $v_{i}$ ,提取节点在最后一层的嵌入 $F_{k,i}^{L} = Z[i, k]$
-
目的:获取节点的高层特征嵌入
-
-
Step5:
-
操作内容:计算节点重要性得分 $\psi_{i} = ReLU\left( \sum_{k} \tilde{w}_{k} F_{k,i}\right)$
-
目的:得到每个节点的重要性,为数据增强提供依据
-
-
Step6:
-
操作内容:输出节点重要性得分集合 $\{\psi_{i}\}$
-
目的:完成 SAM 解释过程
-
2.3 解释引导的对比视图生成(Explanation-Guided Contrastive Views Generation)
1. 设计原则
2. 边扰动(Edge Perturbation)
1)核心逻辑
2)关键公式与操作
- 边重要性计算: $\phi_{i,j} = (\psi_{i} + \psi_{j}) / 2$ ,其中 $\psi_{i}$ 和 $\psi_{j}$ 分别为边 $e_{i,j}$ 两端节点 $v_{i}$ 和 $v_{j}$ 的重要性得分,取平均值作为边的重要性。
- 边掩码生成:
- 掩码 $M^{edge,1}$ : $M_{i,j}^{edge,1} = \begin{cases} 1, & if \phi_{i,j} > \theta_{e} \\ Bernoulli(\phi_{i,j}), & if \phi_{i,j} \leq \theta_{e} \end{cases}$
- 掩码 $M^{edge,2}$ : $M_{i,j}^{edge,2} = \begin{cases} 1, & if \phi_{i,j} > \theta_{e} \\ 1 - M_{i,j}^{edge,1}, & if \phi_{i,j} \leq \theta_{e} \end{cases}$
- 符号含义: $\theta_{e}$ 为边重要性阈值, $Bernoulli(\phi_{i,j})$ 表示以概率 $\phi_{i,j}$ 取 1、 $1 - \phi_{i,j}$ 取 0 的伯努利分布。
- 新视图邻接矩阵: $A_{1} = A \odot M^{edge,1}$ , $A_{2} = A \odot M^{edge,2}$ ,其中 $\odot$ 为哈达玛积, $A$ 为原始邻接矩阵, $A_1$ 和 $A_2$ 为两个新视图的邻接矩阵。
3)阈值 $\theta_{e}$ 的设定
- 公式: $\theta_{e} = \mu_{\phi} + \lambda_{e} * \sigma_{\phi}$
- 符号含义: $\mu_{\phi}$ 为所有边重要性得分的均值, $\sigma_{\phi}$ 为标准差, $\lambda_{e}$ 为超参数,用于根据不同数据集调整重要边的比例(因不同数据集的重要性得分范围不同)。
3. 特征扰动(Feature Perturbation)
1)核心逻辑
2)关键公式与操作
- 特征掩码生成:
- 掩码 $M^{feat,1}$ : $M_{i,d}^{feat,1} = \begin{cases} 1, & if \psi_{i} > \theta_{f} \\ Bernoulli(\psi_{i}), & if \psi_{i} \leq \theta_{f} \end{cases}$
- 掩码 $M^{feat,2}$ : $M_{i,d}^{feat,2} = \begin{cases} 1, & if \psi_{i} > \theta_{f} \\ 1 - M_{i,d}^{feat,1}, & if \psi_{i} \leq \theta_{f} \end{cases}$
- 符号含义: $\theta_{f}$ 为节点特征重要性阈值, $M_{i,d}$ 表示节点 $v_{i}$ 第 $d$ 个特征维度的掩码值, $\psi_{i}$ 为节点 $v_{i}$ 的重要性得分。
- 新视图特征矩阵: $X_{1} = X \odot M^{feat,1}$ , $X_{2} = X \odot M^{feat,2}$ ,其中 $X$ 为原始特征矩阵, $X_1$ 和 $X_2$ 为两个新视图的特征矩阵。
3)阈值 $\theta_{f}$ 的设定
- 公式: $\theta_{f} = \mu_{\psi} + \lambda_{f} * \sigma_{\psi}$
- 符号含义: $\mu_{\psi}$ 为所有节点重要性得分的均值, $\sigma_{\psi}$ 为标准差, $\lambda_{f}$ 为超参数,用于调整重要节点的比例。
4. 视图生成的核心优势
- 信息保留:确保两个视图均保留图中的关键任务相关信息,避免随机扰动导致的结构破坏。
- 互信息控制:通过非重要部分的差异化扰动( $M^{edge,2}$ 与 $M^{edge,1}$ 、 $M^{feat,2}$ 与 $M^{feat,1}$ 在非重要区域互补),降低两个视图的互信息,满足对比学习对视图差异性的要求。
2.4 理论证明(Theoretical Justification)
1. 核心目标
2. 关键定义
|
定义名称
|
定义内容
|
含义与作用
|
|
冗余性(Redundancy)
|
视图 $U_1$ 相对于视图 $U_2$ 对 $y$ 是冗余的,当且仅当 $I(U_1; y | U_2) = 0$
|
若 $U_1$ 与 $U_2$ 互冗余,则 $U_2$ 已包含 $U_1$ 中所有与 $y$ 相关的信息,保证两个视图均含任务相关信息
|
|
充分对比表示(Sufficient Contrastive Representation)
|
视图 $U_1$ 的表示 $z_1$ 对 $U_2$ 是充分的,当且仅当 $I(z_1; U_2) = I(U_1; U_2)$
|
表示 $z_1$ 完整保留了 $U_1$ 中与 $U_2$ 相关的信息,为后续保留跨视图共享的任务相关信息奠定基础
|
|
最小充分对比表示(Minimal Sufficient Contrastive Representation)
|
若 $z_1$ 是 $U_1$ 的充分对比表示,且不存在其他充分对比表示 $z_1'$ 满足 $I(z_1'; X) < I(z_1; X)$ ,则 $z_1$ 是最小充分对比表示
|
最小充分对比表示在保留跨视图共享信息的同时,最大化去除冗余信息,是对比学习追求的理想表示(如图 3 (c) 所示, $z_1^*$ 仅含 $U_1$ 与 $U_2$ 共享的信息)
|
3. 核心理论推导与结论
1)对比视图质量与表示任务相关性的关联
-
前提:若 $U_1$ 与 $U_2$ 互冗余( $I(U_1; y | U_2) = 0$ ),且 $z_1$ 是 $U_1$ 的充分对比表示( $I(z_1; U_2) = I(U_1; U_2)$ ),则 $I(z_1; y) = I(U_1; y)$ 。
-
结论:只要对比视图 $U_1$ 与 $U_2$ 互冗余,且表示 $z_1$ 是充分对比表示,就能保证 $z_1$ 完整保留 $U_1$ 中的任务相关信息,证明解释引导的视图生成(确保互冗余)能为表示提供任务相关性保障。
2)解释引导增强对冗余信息的去除作用
- 逻辑链:
- 对比学习训练目标是使表示 $z_1 \approx z_1^*$ ( $z_1^*$ 为 $U_1$ 的最小充分对比表示),此时 $I(z_1; z_2) \approx I(U_1; U_2)$ ,即表示仅保留跨视图共享信息。
- ENGAGE 框架中,通过调整 $\theta_e$ 和 $\theta_f$ (如提高阈值),可进一步删除 $U_1$ 和 $U_2$ 中的冗余信息,使 $I(U_1; U_2)$ 降低,进而使训练后的 $I(z_1; z_2)$ 降低。
- 由于 $U_1$ 与 $U_2$ 仍互冗余, $I(z_1; y)$ 不受影响,因此 $I(z_1; X) = I(z_1; y) + I(z_1; X | y)$ 中, $I(z_1; X | y)$ (冗余信息)随 $I(z_1; z_2)$ 降低而减少(如图 3 (d) 所示, $z_1^*$ 的冗余信息进一步减少)。
- 结论:解释引导的数据增强可通过调整阈值,在保留任务相关信息( $I(z_1; y)$ 不变)的同时,减少表示中的冗余信息( $I(z_1; X | y)$ 降低),最终提升下游任务性能。
4. 理论与方法的衔接
-
SAM 的作用:通过局部平滑降低单一图 / 节点解释的噪声,确保识别的 “重要信息” 更接近真实任务相关信息,为 $U_1$ 与 $U_2$ 互冗余提供保障。
-
增强策略的作用:基于重要性得分的扰动策略,在生成视图时精准保留重要信息、扰动冗余信息,实现 $I(U_1; U_2)$ 的可控调整,为最小充分对比表示的学习提供高质量视图。
3 Experiments
3.1 实验核心目标与研究问题
-
- RQ1:ENGAGE 在构建对比视图与学习图表示方面的有效性如何?
-
- RQ2:解释机制对表示学习的具体影响是什么?
-
- RQ3:超参数(如 $\lambda_e$ 、 $\lambda_f$ )对 ENGAGE 性能的影响如何?
3.2 实验设置(Experimental Setup)
3.2.1 数据集选择
覆盖图级分类和节点级分类两大任务,确保实验的全面性与代表性,具体数据集如下:
|
任务类型
|
数据集
|
数据特点
|
数量规模
|
任务目标
|
|
图级分类
|
NCI1、PROTEINS、DD、PTC-MR、COLLAB、RDT-B、RDT-M5K、IMDB-B
|
均来自 TUDataset(图学习常用基准库),涵盖分子图(如 NCI1、PROTEINS)、生物图(如 DD)、社交 / 文档图(如 COLLAB、IMDB-B)等不同场景
|
单数据集图数量从数百到数千不等(如 PTC-MR 约 340 个图,COLLAB 约 5000 个图)
|
判断图所属类别(如分子是否具有抗癌活性、蛋白质结构类别)
|
|
节点级分类
|
Cora、CiteSeer、Wiki-CS、Amazon-Computers、Amazon-Photo
|
经典节点分类数据集,涵盖学术网络(Cora、CiteSeer)、维基百科分类网络(Wiki-CS)、电商商品网络(Amazon-Computers/Photo)
|
单数据集节点数量从数千到数万不等(如 Cora 约 2700 个节点,Amazon-Photo 约 7000 个节点)
|
判断节点所属类别(如论文主题、商品类别)
|
3.2.2 对比方法(Baselines)
分为 5 大类,全面覆盖不同时期、不同类型的图表示学习方法,确保对比的公平性与说服力:
|
类别
|
具体方法
|
方法特点
|
备注
|
|
图核方法
|
WL(Weisfeiler-Lehman)、DGK(Deep Graph Kernel)
|
传统图分类方法,基于图的拓扑结构或子结构计算相似度,无神经网络依赖
|
图级分类任务的基础对比基准
|
|
传统无监督图表示学习
|
node2vec、sub2vec、graph2vec
|
基于随机游走(node2vec)或子图嵌入(sub2vec/graph2vec),将图 / 节点转化为向量
|
验证 ENGAGE 相对传统无监督方法的优势
|
|
主流图对比学习
|
GraphCL、JOAO、JOAO(v2)、SimGRACE、MVGRL、InfoGraph、DGI(Deep Graph Infomax)
|
近年主流对比学习或互信息最大化方法,部分采用随机数据增强(如 GraphCL)、自动增强策略(如 JOAO)或无增强(如 SimGRACE)
|
验证 ENGAGE 相对现有对比学习方法的性能提升
|
|
基于随机扰动的对比学习
|
RD-SimCLR、RD-Simsiam
|
ENGAGE 的 “基准版本”:采用与 ENGAGE 相同的 SimCLR/Simsiam 框架,但数据增强为随机扰动(随机删边、随机掩码特征)
|
直接验证 “解释引导增强” 相对 “随机增强” 的核心优势
|
|
其他先进方法
|
GCA(Graph Contrastive Learning with Adaptive Augmentation)、GRACE(Deep Graph Contrastive Representation Learning)
|
自适应增强(GCA)或经典图对比学习(GRACE),部分方法针对节点级任务优化
|
节点级分类任务的关键对比基准
|
3.2.3 模型架构与训练配置
- 编码器(Encoder):根据任务类型选择主流 GNN 架构,确保兼容性验证:
- 图级分类:GIN(Graph Isomorphism Network)—— 对图结构变化敏感,适合图级特征提取;
- 节点级分类:GCN(Graph Convolutional Network)、GAT(Graph Attention Network)—— 分别代表 “基于卷积” 和 “基于注意力” 的节点嵌入方法。
- 对比学习框架:基于 SimCLR 和 Simsiam 修改适配图数据:
- SimCLR:需构建正负样本,采用 NTXent 损失(公式 1),含 1 个 MLP 投影头( $p_o(\cdot)$ );
- Simsiam:无需负样本,采用余弦相似度损失(公式 2),含 2 个 MLP 投影头( $p_o(\cdot)$ 、 $q_o(\cdot)$ )。
- 下游分类器:
- 图级分类:SVM(支持向量机),使用 5 折交叉验证评估;
- 节点级分类:逻辑回归,使用 5 折交叉验证评估。
- 评估指标:准确率(Accuracy),报告 5 次独立实验的 均值 ± 标准差(如 82.97 ± 0.20),“-” 表示该方法在对应数据集上无公开结果。
3.2.4 实验内容与结果分析
1. 核心实验 1:图级分类任务
1)实验内容
在 8 个 TUDataset 数据集上,对比 ENGAGE(EG-SimCLR、EG-Simsiam)与所有 Baselines 的分类准确率,计算各方法的平均排名(A.R.)(排名越低性能越好)。
2)实验结果

3)实验结论
- 性能优势:ENGAGE(EG-SimCLR/EG-Simsiam)在图级分类任务中表现最优,平均排名分别为 2.12 和 2.38,显著优于所有 Baselines;
- 增强有效性:相比 “随机增强” 的 RD 系列,ENGAGE 平均提升 2.90%,其中 NCI1 数据集提升最大(+3.95%),证明 “解释引导增强” 能有效避免随机扰动破坏图结构;
- 稳定性提升:ENGAGE 的标准差更小(如 EG-SimCLR 在 RDT-B 的标准差为 0.46,RD-SimCLR 为 5.40),说明解释引导降低了表示学习的随机性,提升模型稳定性。
2. 核心实验 2:节点级分类任务
1)实验内容
在 5 个节点分类数据集上,对比 ENGAGE(EG-SimCLR、EG-Simsiam,分别搭配 GCN/GAT 编码器)与 Baselines 的分类准确率,计算平均排名
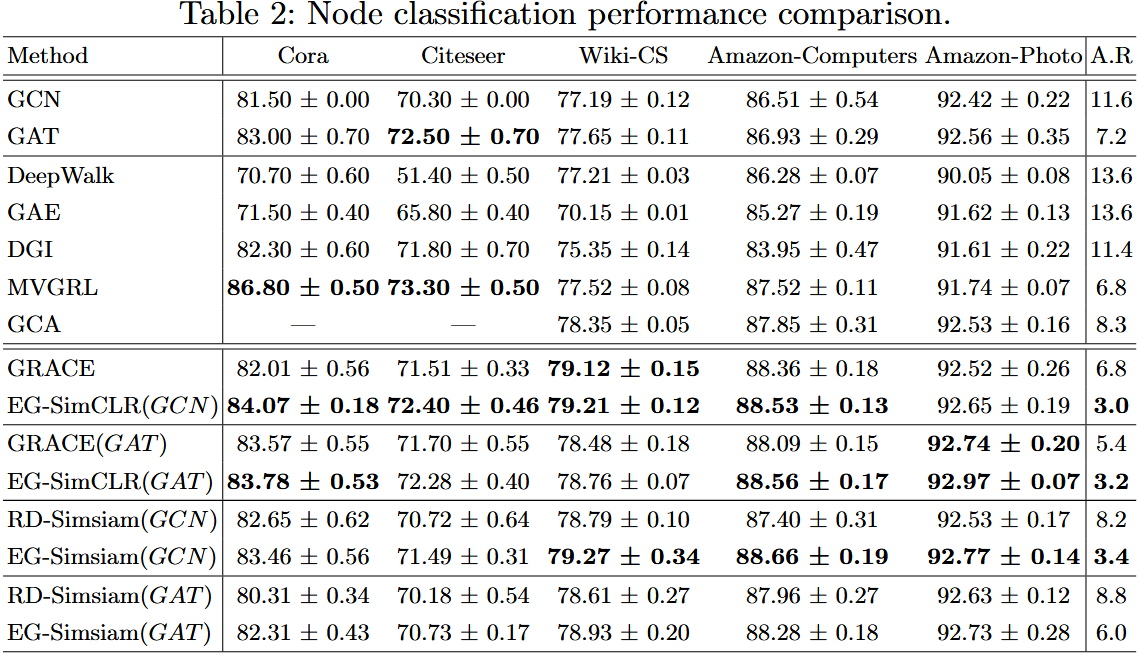
2)实验结果(关键数据来自 Table 2)
3)实验结论
- 跨任务有效性:ENGAGE 在节点级分类任务中仍保持最优性能,平均排名 3.0~3.4,证明其适用于不同粒度的图学习任务;
- 编码器兼容性:ENGAGE 可与 GCN、GAT 等不同 GNN 编码器适配,其中在 GCN 上提升更显著(GAT 自带注意力选择,与 ENGAGE 的 “解释引导” 存在部分功能重叠);
- 性能稳定性:ENGAGE 的标准差普遍小于 Baselines(如 EG-SimCLR 在 Cora 的标准差 0.18,GRACE 为 0.56),进一步验证其鲁棒性。
3. 消融实验:验证解释机制的作用
1)实验内容
设计 4 组对比模型,孤立 “局部平滑”(SAM 的核心创新)和 “解释引导” 两个关键因素,验证其必要性:
-
- RD 系列:随机增强(无解释);
-
- HG 系列:“热图引导增强”(用节点重要性热图引导,但无局部平滑);
-
- EG 系列:ENGAGE(热图引导 + 局部平滑,即 SAM)。
2)实验结果
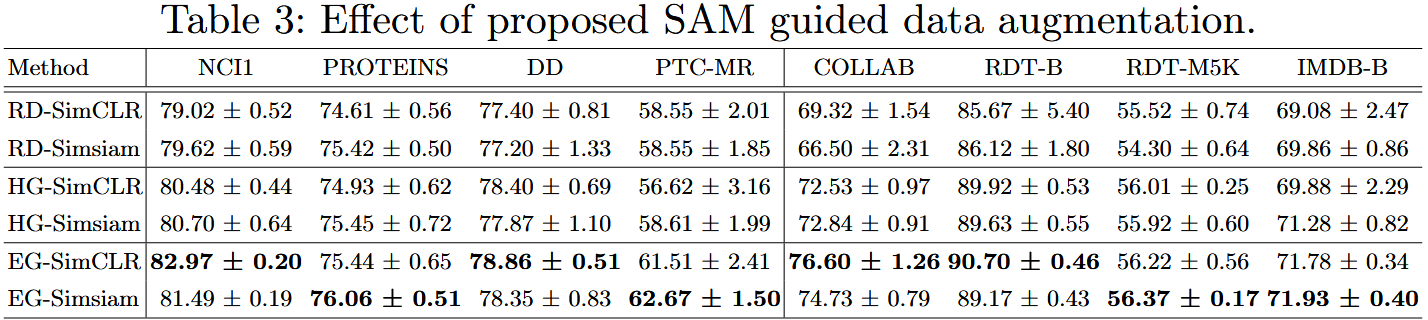
| 方法 | NCI1 准确率 | PROTEINS 准确率 | DD 准确率 | 核心差异 |
| RD-SimCLR | 79.02±0.52 | 74.61±0.56 | 77.40±0.81 | 无解释 |
| HG-SimCLR | 80.48±0.44(+1.46%) | 74.93±0.62(+0.32%) | 78.40±0.69(+1.00%) | 有解释,无局部平滑 |
| EG-SimCLR | 82.97±0.20(+3.95%) | 75.44±0.65(+0.83%) | 78.86±0.51(+1.46%) | 有解释 + 局部平滑 |
3)实验结论
- 解释引导的必要性:HG 系列(有解释)均优于 RD 系列(无解释),平均提升 0.93%,证明 “基于解释的增强” 比 “随机增强” 更有效;
- 局部平滑的价值:EG 系列(有解释 + 局部平滑)优于 HG 系列(有解释无平滑),平均提升 1.21%,证明 SAM 的 “局部平滑” 能降低单一节点 / 图的噪声,提升解释准确性,进而优化增强效果。
4. 消融实验:验证冗余信息去除能力
1)实验内容
定义 “解释稀疏性” 指标( $S = \frac{1}{|V_n|}\sum_{i \in V_n} \mathbb{1}(\psi_i > \bar{\psi})$ ,其中 $\bar{\psi}$ 为节点重要性均值, $\mathbb{1}(\cdot)$ 为指示函数),观察训练过程中稀疏性的变化:
- 激进扰动: $\lambda_e=2, \lambda_f=2$ (高阈值,更多冗余信息被删除);
- 温和扰动: $\lambda_e=-2, \lambda_f=-2$ (低阈值,保留更多信息)。
2)实验结果
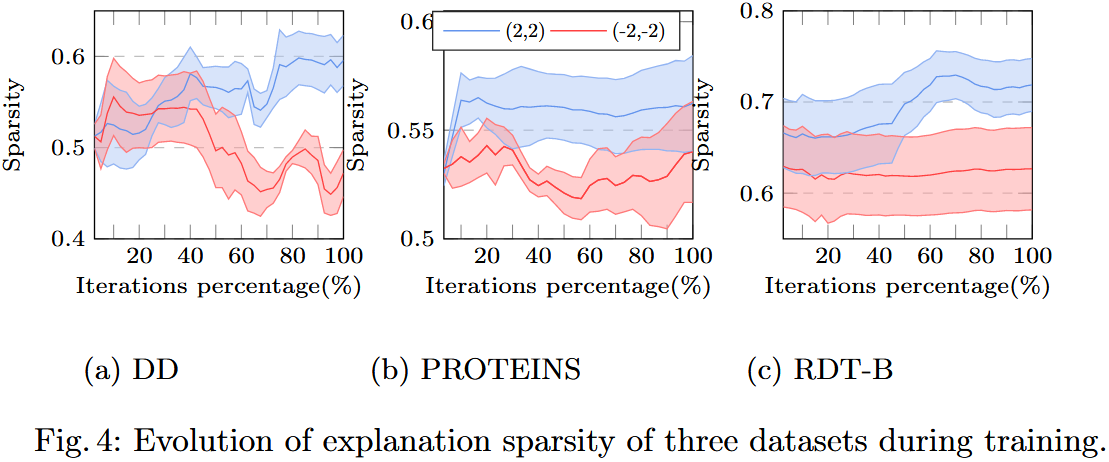
| 数据集 | 激进扰动( $\lambda=2$ )稀疏性变化 | 温和扰动( $\lambda=-2$ )稀疏性变化 |
| DD | 训练过程中从 0.55 升至 0.70(上升 27%) | 基本稳定在 0.55 左右(波动 < 2%) |
| PROTEINS | 从 0.50 升至 0.65(上升 30%) | 稳定在 0.50~0.52(波动 < 4%) |
| RDT-B | 从 0.60 升至 0.75(上升 25%) | 稳定在 0.60~0.62(波动 < 3%) |
3)实验结论
- 冗余信息去除:激进扰动下,解释稀疏性显著上升(仅少数节点被判定为 “重要”),证明 ENGAGE 能逐步删除冗余信息,符合 “信息瓶颈原理”;
- 扰动强度控制:温和扰动下稀疏性稳定,说明阈值调整可控制信息保留程度,适配不同数据集的需求。
5. 超参数分析: $\lambda_e$ 与 $\lambda_f$ 的影响
1)实验内容
在 13 个数据集(8 个图级 + 5 个节点级)上,测试 $\lambda_e$ (边扰动阈值系数)和 $\lambda_f$ (特征扰动阈值系数)取不同值(-3~3)时的模型准确率,计算 “性能差距”(最优准确率 - 最差准确率)。
2)实验结果(关键数据来自 Figure 5)
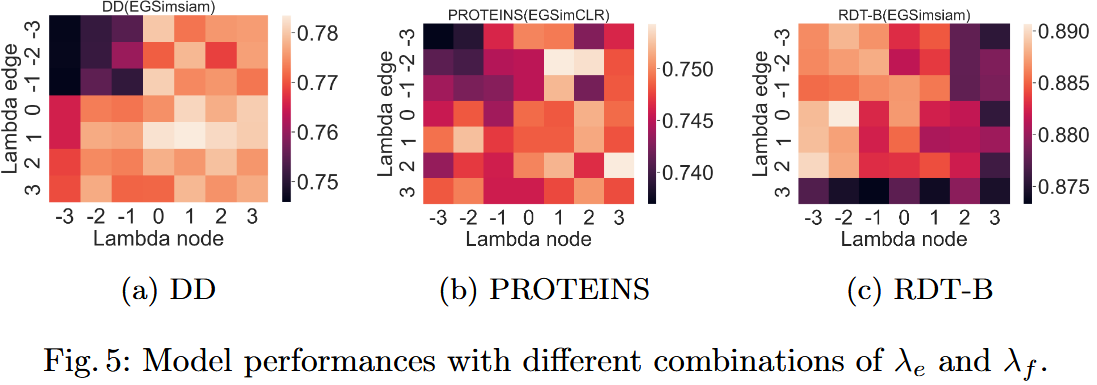
| 数据集 | 最优 $\lambda$ 组合 | 性能差距 | 敏感性分析 |
| DD(图级) | $\lambda_e=2, \lambda_f=2$ (激进扰动) | 3.5% | 对高 $\lambda$ 更敏感(性能提升明显) |
| PROTEINS(图级) | $\lambda_e=0, \lambda_f=0$ (中等扰动) | 2.1% | 对 $\lambda$ 变化不敏感(性能波动小) |
| RDT-B(图级) | $\lambda_e=-1, \lambda_f=-1$ (温和扰动) | 1.8% | 对低 $\lambda$ 更敏感(激进扰动性能下降) |
| COLLAB(图级) | $\lambda_e=1, \lambda_f=1$ | 9.55%(最大差距) | 对 $\lambda$ 极敏感,需精细调参 |
| Amazon-Photo(节点级) | $\lambda_e=0, \lambda_f=0$ | 0.23%(最小差距) | 对 $\lambda$ 不敏感,鲁棒性强 |
| 模型框架对比 | Simsiam-based 模型平均性能差距 3.39%(图级)、0.75%(节点级) | 均小于 SimCLR-based 模型(3.96%、1.08%) | Simsiam 框架对超参数更鲁棒 |
3)实验结论
- 数据集依赖性:不同数据集的最优 $\lambda$ 组合不同(如 DD 适合激进扰动,RDT-B 适合温和扰动),因数据集本身的 “冗余信息含量” 不同;
- 敏感性差异:部分数据集(如 COLLAB)对超参数极敏感,需针对性调参;部分数据集(如 Amazon-Photo)鲁棒性强,调参成本低;
- 框架优势:Simsiam-based 模型的超参数敏感性低于 SimCLR-based,因 Simsiam 无需负样本,避免了负样本质量受扰动影响的问题。
3.2.5 实验总结论
- 有效性:ENGAGE 在图级和节点级分类任务中均取得最优性能,相比随机增强方法平均提升 2.90%(图级)和 1.00%(节点级),证明 “解释引导数据增强” 是解决图对比学习中 “随机扰动破坏结构” 问题的有效方案;
- 核心创新价值:SAM 的 “局部平滑” 机制能提升解释准确性,使增强策略更精准,消融实验显示该机制贡献 1.21% 的性能提升;
- 灵活性与鲁棒性:ENGAGE 可适配 GCN、GAT、GIN 等多种编码器,兼容 SimCLR/Simsiam 等对比框架,且在多数数据集上性能稳定(标准差小);
- 超参指导:超参数 $\lambda_e/\lambda_f$ 需根据数据集调整,激进扰动适合冗余信息多的数据集(如 DD),温和扰动适合关键信息密集的数据集(如 RDT-B),Simsiam 框架是超参数敏感场景的优选。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号