EPA-GRL——Explanation-Preserving Augmentation for Semi-Supervised Graph Representation Learning
论文信息
论文标题:Explanation-Preserving Augmentation for Semi-Supervised Graph Representation Learning
论文作者:Gang Liu、Eric Inae、Tengfei Luo、Meng Jiang
论文来源:
发布时间:2024-10-16
论文地址:link
论文代码:link
1 Introduction
1.1 研究背景:图表示学习(GRL)的发展与核心技术
- 领域启发:受视觉、语言领域无监督 / 自监督表示学习进展启发,GRL 在节点分类、图分类任务中性能显著提升,应用覆盖社会科学、分子生物学等多个领域。
- 核心技术:对比学习成为 GRL 主流技术,其核心逻辑为:为每个图生成两个增强视图,目标是让同一图的不同增强视图表示相似,不同图的增强视图表示尽可能区分。
- 关键影响因素:图增强策略是决定 GRL 性能的核心因素。理想的图增强需满足两大条件(类比图像数据增强):
- 语义继承:增强视图需继承原图的核心语义;
- 差异引入:增强视图间需存在足够差异,以支撑鲁棒的表示学习。
1.2 现有方法的局限性:重扰动、轻语义
-
EPA-Aug实现:1)用少量带标签图训练 GNN 分类器,再基于图信息瓶颈原则训练解释器,提取语义子结构。 2)对图的边缘子结构进行受控扰动,结合语义子结构生成 “EPA - Aug” 图;
-
核心问题:多数现有 GRL 增强方法(如 GraphCL、JOAO)仅关注通过结构扰动引入差异,却严重忽视语义保留需求。
- 具体表现:这些方法通过随机删边、删点、特征掩码、子图提取等方式生成增强图,其随机性会大幅改变图的重要(子)结构或特征,导致语义大量丢失,最终影响下游任务性能。
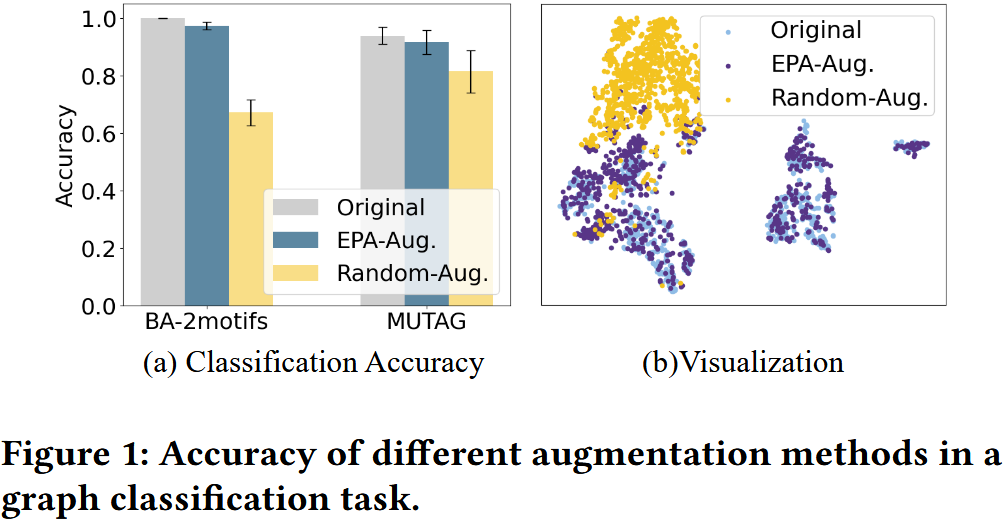
- 实验佐证(图 1):
- 实验设计:用 GNN 分类器在基准数据集(BA-2motifs、MUTAG)训练集上训练后,分别在测试集原图、“Random-Aug”(随机删点的语义无关增强)图、“EPA-Aug”(语义保留增强)图上评估准确率。
- 结果 1(分类准确率):GNN 在原图上准确率高,但在 “Random-Aug” 图上准确率骤降(语义丢失显著),在 “EPA-Aug” 图上准确率接近原图(语义保留有效)。
- 结果 2(嵌入分布):“Random-Aug” 图的嵌入分布与原图差异极大,而 “EPA-Aug” 图既能保留原图嵌入分布,又能引入合理差异,证明语义保留增强对 GRL 性能提升的潜力。
1.3 现有改进方法的不足
- MoCL:通过生物等排体替换分子图中的有效子结构(子结构性质相似),但依赖昂贵的领域知识,无法自然扩展到社会图等其他领域。
- SimGRACE:规避图结构扰动,转而扰动 GNN 参数,用扰动后的 GNN 生成增强图。虽未显式修改图结构,但会通过任意改变图嵌入间接导致无约束的结构变化,无法保证语义保留。
1.4 研究动机与目标
- 语义特殊性:与图像语义可直观观察不同,图的语义难以可视化且具有类别特异性,无法直接借助人类先验设计扰动策略。
- 核心目标:开发基于少量带标签样本训练的语义保留增强技术,以改进 GRL 性能。
- 与相关工作的区别:现有监督图对比学习方法(如 [13,14])需大量带标签样本确定正样本对,而非利用类别信号显式保留语义,与本文 “少量标签实现语义保留” 的目标不同。
1.5 本文方法:EPA-GRL 的核心思路
- 灵感来源:基于图可解释 AI(XAI)研究,图解释方法能学习参数化解释器,识别原图中区分不同类别、承载核心语义的子结构(如分子中的苯环)。
- 方法设计:提出解释保留增强 GRL(EPA-GRL),分两阶段实现语义保留与数据扰动的平衡:
- 预训练阶段:用少量类别标签训练图解释器;
- GRL 阶段:对每个输入图,用解释器提取语义子结构(保持不变),对剩余的边缘子结构进行扰动,结合两者生成增强图,再输入对比学习框架学习表示。
- 框架属性:利用少量带标签图和大量无标签图,构建新型半监督 GRL 框架。
1.6 本文主要贡献
- 问题识别:通过回顾数据增强的两大标准,指出现有 GRL 增强方法的核心局限;首次探索少量类别标签在 GRL 语义保留中的潜力。
- 方法创新:提出半监督 GRL 框架,引入 XAI 技术设计新型增强方法 EPA,实现语义保留式扰动。
-
理论支撑:通过分析示例从理论上证明:在语义保留增强与语义无关增强下,GRL 模型输出嵌入的经验风险最小化(ERM)准确率差距可任意大。
-
实验验证:在 6 个基准数据集上进行大量实验,对比多种增强方法和对比学习框架,验证 EPA-GRL 的有效性(尤其在标签有限场景下)。
2 Method
2.1 Pre-Training GNN Explainer(预训练 GNN 解释器)
2.1.1 核心目标
2.1.2 两步训练流程
步骤 1:训练基础 GNN 分类器($f_{pt}$)
- 输入数据:小规模带标签数据集 $T_\ell = \{(G_i, Y_i) | i \in [M]\}$,其中 $G_i$ 为图,$Y_i$ 为对应的类别标签。
- 训练目标:让 GNN 分类器学习图的结构特征与类别之间的映射关系,具备区分不同类别图的能力。
- 损失函数:采用交叉熵损失,最小化模型预测标签与真实标签的差异,公式如下:
$ \underset{f_{pt}}{arg min }\left(\sum_{(G, y) \in \mathcal{T}_\ell}-y \log \left(f_{pt}(G)\right)\right) $
其中,$f_{pt}(G)$表示 GNN 分类器对图$G$的类别预测结果,$y$为图$G$的真实标签。
- 作用:为后续解释器的训练提供一个具备类别区分能力的基准模型,解释器需基于该模型的预测逻辑提取关键子结构。
步骤 2:训练 GNN 解释器($\Psi(\cdot)$)
- 输入数据:训练好的基础 GNN 分类器 $f_{pt}$、带标签数据集$T_\ell$。
- 解释器输出:对于输入图 $G=(A, X)$( $A$为邻接矩阵,$X$ 为节点特征矩阵),解释器生成一个二进制掩码 $M$,通过 $(X, A \odot M)$ 得到解释子图 $G^{(\exp)}$ 。其中 $M_{i,j}=1$ 表示边 $(i,j)$ 被保留在解释子图中,$M_{i,j}=0$ 则表示该边被剔除。
- 训练原则:遵循图信息瓶颈(GIB)原则,即最优的解释子图需在 “保留足够预测信息” 和 “保持结构紧凑” 之间取得平衡。前者确保子图能反映图的核心语义,后者避免引入冗余结构导致过拟合。
- 损失函数:综合考虑语义保留和结构紧凑性,公式如下:
$ \underset{\Psi}{arg min }\left(\sum_{(G, y) \in \mathcal{T}_\ell} CE\left(Y ; f_{pt}(\Psi(G))\right)+\lambda|\Psi(G)|\right) \tag{2} $
其中:
-
-
-
$CE(\cdot;\cdot)$ 为交叉熵损失,衡量 GNN 分类器对解释子图 $\Psi(G)$ 的预测精度(语义保留指标);
-
$|\Psi(G)|$表示解释子图的大小(可用边数或边权重总和衡量,结构紧凑指标);
-
$\lambda$ 为超参数,用于调节 “语义保留” 与 “结构紧凑” 两项的权重;
-
-
- 效率设计:采用生成式解释器(参数化神经网络),基于节点嵌入学习掩码 $M$。训练完成后,该解释器可直接应用于无标签数据集 $T_u$,为无标签图生成解释子图,无需额外训练。
2.2 Explanation-Preserving Augmentation Enhanced Graph Representation Learning(解释保留增强的图表示学习)
2.2.1 核心背景与目标
2.2.2 解释保留增强策略(EPA)
核心逻辑
五种具体增强方法
|
增强方法(Data Augmentation)
|
操作对象
|
具体操作步骤
|
核心假设(Underlying Prior)
|
|
Node Dropping(节点删除)
|
节点、边
|
1. 从边缘子图$\Delta G$的节点集中,按独立同分布(i.i.d.)均匀概率随机选择部分节点;
2. 删除选中节点及其关联的所有边。
|
非关键节点的缺失对图的核心语义影响极小,不会改变图的类别属性。
|
|
Edge Dropping(边删除)
|
边
|
1. 遍历边缘子图$\Delta G$的所有边;
2. 按 i.i.d. 均匀概率随机删除部分边,不改变节点集。
|
图的语义对非关键边的连接状态不敏感,边缘子图的边扰动不会破坏核心语义。
|
|
Attribute Masking(属性掩码)
|
节点 / 边属性
|
1. 生成一个二进制掩码矩阵$M^{(smp)}$,矩阵元素按 i.i.d. 均匀概率取值(1 表示保留属性,0 表示掩码);
2. 将掩码矩阵与边缘子图$\Delta G$的节点 / 边特征矩阵进行点乘,掩盖部分属性。
|
非关键属性的丢失不会影响模型对图核心语义的识别,边缘子图的属性扰动可引入方差且不破坏语义。
|
|
Subgraph(子图采样)
|
节点、边
|
1. 从边缘子图$\Delta G$中随机选择一个初始节点;
2. 基于初始节点进行随机游走,不断扩展节点集,直到采样节点数达到预设比例;
3. 保留采样节点及节点间的所有边,形成采样子图。
|
从边缘子图中采样局部连通子图,可改变图的局部结构以引入方差,但不会破坏图的整体语义完整性。
|
|
Mixup(混合增强)
|
节点、边
|
1. 从当前批次的图中随机选择另一个图$G'$;
2. 提取$G'$的边缘子图$\Delta G'$;
3. 将原始图$G$的解释子图$G^{(\exp)}$与$\Delta G'$组合,形成增强图。
|
解释子图是图语义的核心,与其他图的边缘子图混合后,仍能保持原始图的核心语义,同时引入新的结构方差。
|
注:每种增强方法的详细伪代码见原文附录 B.1。
2.2.3 图表示学习框架
A. 通用前置流程
- 生成增强视图:对数据集中的每个图 $G$,采用两种不同的 EPA 增强方法,生成两个增强视图 $G_1$ 和 $G_2$ 。
- 嵌入生成与映射:
- 将增强视图输入图编码器 $f_{enc}$(可采用 GCN、GIN 等任意 GNN 架构),得到图级嵌入 $h_1 = f_{enc}(G_1)$ 和 $h_2 = f_{enc}(G_2)$;
- 引入投影头 $f_{pro}$(采用 MLP 结构),将编码器输出的嵌入映射为新表示 $z_1 = f_{pro}(h_1)$ 和 $z_2 = f_{pro}(h_2)$ 。其中 $z_1$ 和 $z_2$ 仅用于训练阶段的损失计算,下游任务(如节点分类、图分类)直接使用编码器输出的 $h_1$ 或 $h_2$ 作为图表示。
B. 基于 GraphCL 的对比学习
- 核心思想:最大化同一图的不同增强视图之间的互信息,同时最小化不同图的增强视图之间的互信息,通过噪声对比估计区分正负样本(同一图的两个视图为正样本对,不同图的视图为负样本对)。
- 损失函数:对于批次大小为 $N$ 的数据集,第 $i$ 个图的两个增强视图投影嵌入为 $z_{i,1}$ 和 $z_{i,2}$,损失公式如下:
$ \begin{aligned} \ell_{i}^{(graphcl) }=- & \frac{1}{2} \log \frac{\exp \left(sim\left(z_{i,1}, z_{i,2}\right) / \tau\right)}{\sum_{j=1}^{N} \exp \left(sim\left(z_{i,1}, z_{j,2}\right) / \tau\right)} \\ & -\frac{1}{2} \log \frac{\exp \left(sim\left(z_{i,2}, z_{i,1}\right) / \tau\right)}{\sum_{j=1}^{N} \exp \left(sim\left(z_{i,2}, z_{j,1}\right) / \tau\right)}, \end{aligned} \tag{3} $
其中,
-
-
-
$sim(\cdot,\cdot)$为余弦相似度函数,用于衡量嵌入向量的相似性;
-
$\tau$为温度参数,调节相似度分布的平滑程度,避免梯度消失或爆炸。
-
-
-
最终损失:对批次内所有图的损失求和,作为模型训练的总损失。
C. 基于 SimSiam 的对比学习
- 核心特点:无需构建负样本对,通过 “预测头 + 停止梯度(stopgrad)” 机制,避免模型学习到 trivial 表示(如所有嵌入向量趋同),简化训练流程。
- 损失计算流程:
-
预测头映射:对两个增强视图的投影嵌入 $z_1$ 和 $z_2$,分别通过 MLP 预测头生成预测向量:
$ p_1 = MLP(z_1), \quad p_2 = MLP(z_2) \tag{4} $
-
停止梯度操作:对其中一个投影嵌入施加停止梯度(stopgrad),即 $stopgrad(z_1)$ 和 $stopgrad(z_2)$ ,阻断该路径的梯度传播,将其视为 “固定目标”。
-
负余弦相似度损失:最小化预测向量与固定目标之间的负余弦相似度,最大化两者的相似性,公式如下:
$ \begin{aligned} \mathcal{D}\left(p_1, stopgrad(z_2)\right) &= -\frac{p_1}{\left\| p_1\right\| _{2}} \cdot \frac{stopgrad(z_2)}{\left\| stopgrad(z_2)\right\| _{2}} \\ \mathcal{D}\left(p_2, stopgrad(z_1)\right) &= -\frac{p_2}{\left\| p_2\right\| _{2}} \cdot \frac{stopgrad(z_1)}{\left\| stopgrad(z_1)\right\| _{2}} \end{aligned} \tag{5} $
- 最终损失:对两个方向的损失取平均,作为总损失:
$ \ell^{(simsiam)}=\frac{1}{2} \mathcal{D}\left(p_1, stopgrad(z_2)\right)+\frac{1}{2} \mathcal{D}\left(p_2, stopgrad(z_1)\right) \tag{6} $
- 关键作用:停止梯度操作防止编码器直接优化相似性目标,迫使模型从图的结构和特征中学习有意义的语义表示,避免表示坍缩。
3 Experiments
3.1 实验核心目标
验证所提出的EPA-GRL(解释保留增强的图表示学习)框架的有效性,具体包括:
-
-
对比 EPA 增强方法与传统语义无关增强(Vanilla)的性能差异;
-
将 EPA-GRL 与当前主流图表示学习(GRL)方法对比,验证其优越性;
-
通过消融实验分析标签数量对 EPA-GRL 的影响;
-
结合案例可视化,直观展示 EPA 增强的语义保留效果。
-
3.2 Experimental Setup(实验设置)
3.2.1 Datasets(数据集)
选用 6 个涵盖生化分子、蛋白质领域的基准数据集,部分数据集提供语义子图的 Ground Truth(用于验证语义保留),详细统计如下表(对应原文 Table 5):
|
数据集名称 |
领域 |
图数量(#Graphs) |
平均节点数(Avg.#nodes) |
平均边数(Avg.#edges) |
语义子图数量(#Explanations) |
节点特征数(#Feature) |
类别数(#Classes) |
|
MUTAG |
生化分子 |
2,951 |
30.32 |
30.77 |
1,015 |
14 |
2 |
|
Benzene |
生化分子 |
12,000 |
20.58 |
43.65 |
6,001 |
14 |
2 |
|
Alkane-Carbonyl |
生化分子 |
4,326 |
21.13 |
44.95 |
375 |
14 |
2 |
|
Fluoride-Carbonyl |
生化分子 |
8,671 |
21.36 |
45.37 |
1,527 |
14 |
2 |
|
D&D |
生物信息(蛋白质) |
1,178 |
284.32 |
715.66 |
0 |
89 |
2 |
|
PROTEINS |
生物信息(蛋白质) |
1,113 |
39.06 |
72.82 |
0 |
3 |
2 |
- 数据集特点:
- MUTAG:按分子对沙门氏菌的致突变性分类;
- Benzene:按分子是否含苯环分类;
- Alkane-Carbonyl/Fluoride-Carbonyl:按分子是否含特定官能团(烷烃 / 羰基、氟原子 / 羰基)分类;
- D&D/PROTEINS:按蛋白质是否为酶(D&D)、按蛋白质结构功能(PROTEINS)分类。
- 数据划分:所有数据集按 80%/10%/10% 分为训练集、验证集、测试集,下游分类任务(SVM)从训练集中随机采样 50 个图作为训练数据。
3.2.2 Baselines(基准方法)
A. 增强方法基准(Vanilla 系列)
用于对比 EPA 增强与传统语义无关增强的性能,共 5 种:
|
增强方法名称
|
操作逻辑
|
|
Node Dropping(Vanilla)
|
随机删除图中 10% 的节点及关联边(无语义约束)
|
|
Edge Dropping(Vanilla)
|
随机删除图中 10% 的边(无语义约束)
|
|
Attribute Masking(Vanilla)
|
随机掩码图中 10% 的节点特征(无语义约束)
|
|
Subgraph-Sample(Vanilla)
|
从原图中随机游走采样子图(取 50% 节点为起点,游走 10 步)
|
|
Mixup(Vanilla)
|
随机选取批次内另一图,随机裁剪 20% 后与原图组合(无语义约束)
|
B. GRL 方法基准
包括无监督 / 自监督 GRL 方法及其半监督版本(用 50 个标签微调),共 5 种:
|
GRL 方法名称
|
方法特点
|
半监督版本(SS-*)实现方式
|
|
GraphCL
|
自监督对比学习,用 4 种 Vanilla 增强生成视图
|
1. 用无标签图预训练编码器;2. 用 50 个标签微调编码器(交叉熵损失)
|
|
AD-GCL
|
对抗性增强 GRL,通过可训练删边策略避免学习冗余信息
|
同 GraphCL 的半监督流程
|
|
JOAO
|
动态选择增强方法的 GRL,用 min-max 优化调整增强策略
|
同 GraphCL 的半监督流程
|
|
AutoGCL
|
自动 GRL,用可学习视图生成器联合训练 “生成器 - 编码器 - 分类器”
|
原生支持半监督训练(无需分两阶段)
|
|
SimGRACE
|
无增强 GRL,用原编码器与扰动编码器生成两个视图进行对比
|
同 GraphCL 的半监督流程
|
- 额外基准:Supervised(仅用 50 个标签训练 GNN 编码器,无无标签图辅助)。
C. 核心对比逻辑
- EPA 增强 vs Vanilla 增强:固定 GRL 框架(GraphCL/SimSiam),对比增强方法的语义保留效果;
- EPA-GRL vs SOTA GRL:对比 EPA 增强 + GraphCL/SimSiam 与其他 GRL 方法的性能。
3.2.3 Implementation Details
| 实现模块 | 具体配置 |
| 骨干 GNN 模型 | 默认 3 层 GCN,附录验证 3 层 GIN(确保架构通用性) |
| 优化器 | Adam,学习率 1e-3;EPA 解释器训练额外加权重衰减(原文未明确数值) |
| 超参数 | GraphCL 温度参数 $\tau=0.2$ ;增强方法扰动比例(如 Node Dropping 删 10% 节点) |
| 下游分类器 | SVM(用 GRL 生成的图入作为输入) |
| 硬件环境 | Linux 机器,8 张 Nvidia A100-PCIE 40GB GPU,CUDA 12.4 |
| 实验重复性 | 所有实验重复 10 次,结果以 “均值 ± 标准差” 表示 |
3.3 Experimental Results(实验结果)
3.3.1 对比 1:EPA 增强 vs Vanilla 增强
3.3.1.1 基于 GraphCL 框架的结果(原文 Table 2)
- 关键性能提升案例:
- PROTEINS 数据集:EPA-Edge Dropping(0.757±0.055)vs Vanilla-Edge Dropping(0.702±0.077),相对提升 7.83%;
- MUTAG 数据集:EPA-Node Dropping(0.860±0.020)vs Vanilla-Node Dropping(0.803±0.030),绝对提升 5.7%;
- Alkane-Carbonyl 数据集:EPA-Subgraph(0.987±0.019)vs Vanilla-Subgraph(0.973±0.027),绝对提升 1.4%。
- 共性发现:
- 结构类增强(Node/Edge Dropping、Subgraph、Mixup)整体优于属性掩码(Attribute Masking),因结构扰动引入的方差更大;
- EPA 增强对 “语义敏感型扰动”(如 Node Dropping)的改进更明显,因 Vanilla-Node Dropping 易删除语义子图节点,而 EPA 仅删除边缘子图节点。
3.3.1.2 基于 SimSiam 框架的结果(原文 Table 3)
- 关键性能提升案例:
- PROTEINS 数据集:EPA-Subgraph(0.744±0.084)vs Vanilla-Subgraph(0.702±0.068),相对提升 5.98%;
- Fluoride-Carbonyl 数据集:EPA-Edge Dropping(0.640±0.043)vs Vanilla-Edge Dropping(0.618±0.045),绝对提升 2.2%。
- 共性发现:GraphCL 框架整体性能优于 SimSiam,因 GraphCL 通过负样本区分增强了表示的判别性;但 EPA 增强在两种框架下均有效,证明其GRL 框架无关性。
3.3.2 对比 2:EPA-GRL vs SOTA GRL 方法
基于 GraphCL 框架(默认最优),用 50 个标签训练半监督模型,核心结论:EPA-GRL 在多数数据集上排名第一,且性能稳定(原文 Table 4)。
|
数据集
|
最优 GRL 方法
|
准确率(均值 ± 标准差)
|
次优方法(如 SS-GraphCL)
|
准确率差距
|
|
MUTAG
|
EPA-GRL
|
0.861±0.032
|
SS-GraphCL(0.853±0.034)
|
+0.8%
|
|
Benzene
|
EPA-GRL
|
0.765±0.032
|
SS-JOAO(0.762±0.047)
|
+0.3%
|
|
Alkane-Carbonyl
|
EPA-GRL
|
0.982±0.020
|
SS-GraphCL(0.978±0.020)
|
+0.4%
|
|
Fluoride-Carbonyl
|
EPA-GRL
|
0.663±0.028
|
SS-JOAO(0.668±0.033)*
|
-0.5%(次优)
|
|
D&D
|
EPA-GRL
|
0.650±0.065
|
SS-AutoGCL(0.639±0.065)
|
+1.1%
|
|
PROTEINS
|
EPA-GRL
|
0.744±0.065
|
SS-AutoGCL(0.734±0.066)
|
+1.0%
|
- 关键发现:
- 半监督版本(SS-*)均优于其自监督版本,证明少量标签对 GRL 的增益;
- EPA-GRL 性能优于 Supervised 基准(如 MUTAG:EPA-GRL 0.861 vs Supervised 0.848),证明 “无标签图 + EPA 增强” 的价值;
- EPA-GRL 标准差更小(如 PROTEINS:0.065 vs SS-AutoGCL 0.066),因语义保留增强降低了随机扰动的不稳定性。
3.3 对比 3:消融实验(Ablation Analysis)
3.3.1 解释器预训练标签数量的影响(原文 Fig. 4)
- 实验设计:固定 SVM 训练标签数为 50,改变解释器预训练的标签数( $|T_\ell|=50,100,150$ );
- 结果:
- EPA 增强:随 $|T_\ell|$ 增加,所有增强方法的准确率均上升(如 Node Dropping:50 标签 0.84→150 标签 0.87);
- Vanilla 增强:准确率基本不变(如 Node Dropping 始终≈0.82),因无语义学习环节,标签无法提升增强质量。
3.3.2 下游 SVM 训练标签数量的影响(原文 Fig. 5)
-
实验设计:固定解释器预训练标签数为 50,改变 SVM 训练的标签数(从少量到 100);
-
结果:两种增强的准确率均随 SVM 标签数增加而上升,但 EPA 增强始终高于 Vanilla 增强(如 Edge Dropping:EPA 比 Vanilla 高≈0.02),证明 EPA 生成的嵌入质量更高。
3.4 Case Studies(案例研究)
3.4.1 实验设计
3.4.2 核心发现
- EPA 增强:仅扰动边缘子图(灰色节点 / 虚线边均在语义子图外),黄色语义子图完整保留;
- Vanilla 增强:随机扰动语义子图(如 Vanilla-Node Dropping 删除了语义子图中的节点,Vanilla-Edge Dropping 删除了语义子图中的边),导致语义丢失。
- 直观验证:EPA 增强的 “语义保留” 设计有效,解释了其性能优于 Vanilla 增强的原因。
3.5 Additional Analysis(额外分析)
3.5.1 数据集通用性验证
-
- BA-2motifs:EPA 增强平均相对提升 17.3%(如 Node Dropping:Vanilla 0.739→EPA 0.874);
-
- HIV:EPA 增强在多数方法上优于 Vanilla(如 Edge Dropping:Vanilla 0.640→EPA 0.643),证明其在合成 / 大规模数据上的通用性。
3.5.2 GNN 架构通用性验证
-
- MUTAG:EPA-Node Dropping(0.846±0.035)vs Vanilla-Node Dropping(0.843±0.033);
-
- PROTEINS:EPA-Edge Dropping(0.650±0.063)vs Vanilla-Edge Dropping(0.637±0.049);
-
- 结论:EPA 增强在不同 GNN 架构上均有效,证明其架构无关性。
3.5.3 嵌入可视化分析
-
- Vanilla 增强的嵌入分布与原图差异大(分布偏移明显);
-
- EPA 增强的嵌入分布与原图高度一致(保留语义),同时引入足够方差(视图间有差异),验证了 EPA 对 “语义保留” 和 “数据扰动” 的平衡。
3.6 实验小节核心结论
- EPA 增强的有效性:在 6 个基准数据集、2 个 GRL 框架、2 种 GNN 架构上,EPA 增强均优于传统 Vanilla 增强,最大相对提升 7.83%;
- EPA-GRL 的优越性:作为半监督 GRL 框架,EPA-GRL 在多数数据集上优于当前 SOTA 方法(如 GraphCL、AutoGCL),且性能更稳定;
- 标签利用效率:EPA 能有效利用更多标签提升增强质量,而 Vanilla 增强无法利用标签,证明 “语义学习” 对少量标签的高效利用;
- 通用性与灵活性:EPA 增强可集成到任意 GRL 框架(GraphCL/SimSiam),适配任意 GNN 架构(GCN/GIN),适用于合成 / 真实、小规模 / 大规模数据集。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号