蓝桥杯省赛真题——螺旋折线

螺旋折线
如图p1.png所示的螺旋折线经过平面上所有整点恰好一次。
对于整点(X, Y)，我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。
例如dis(0, 1)=3, dis(-2, -1)=9
给出整点坐标(X, Y)，你能计算出dis(X, Y)吗？

【输入格式】
X和Y
对于40%的数据，-1000 <= X, Y <= 1000
对于70%的数据，-100000 <= X， Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000
【输出格式】
输出dis(X, Y)
【样例输入】
0 1
【样例输出】
3

分析

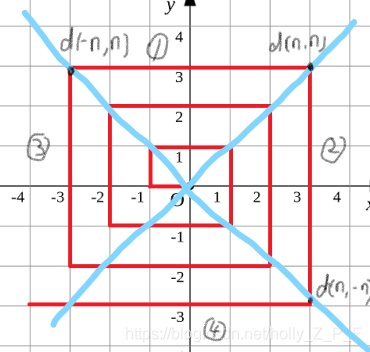
可以很容易观察到：当x=y>=0时，dis(x,y)=dis(x,x)=4*x*x。因此设正整数n，dis(n,n)=4*x*x，dis(-n,n)=4*n*n-2*n，dis(n,-n)=4*n*n+2*n。如图所示将坐标系分为四部分,其中区域①内坐标到原点的距离可以根据坐标到(n,n)的距离与dis(n,n)的值来算。比如dis(x,n)=dis(n,n)-(n-x),|x|<=n。区域②③④同理。

#include<iostream>
using namespace std;
int main()
{
	long long x = 0, y = 0;//坐标
	long long ans = 0;//答案
	cin >> x >> y;
	if (y >= x && y >= -x)//区域1
	{
		ans = y * y * 4 - abs(y) + x;
	}
	else if (y >= x && y <= -x)//区域3
	{
		ans = x * x * 4 - 3 * abs(x) + y;
	}
	else if (y <= x && y >= -x)//区域2
	{
		ans = x * x * 4 + abs(x) - y;
	}
	else if (y <= x && y <= -x)//区域4
	{
		ans = y * y * 4 + 3 * abs(y) - x;
	}
	cout << ans;
	return 0;
}