Logistic回归基础篇之梯度上升算法
代码示例:
import numpy as np import matplotlib.pyplot as plt def loadDataSet(): dataMat = [];labelMat = [] fr = open('testSet.txt') for line in fr.readlines(): lineArr = line.strip().split() dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])]) labelMat.append(int(lineArr[2])) fr.close() return dataMat,labelMat def sigmoid(intX): return 1.0/(1+np.exp(-intX)) def gradAscent(dataMatIn,classLabels): dataMatrix = np.mat(dataMatIn) labelMat = np.mat(classLabels).transpose() m,n = np.shape(dataMatrix) alpha = 0.001 maxCycles = 500 weights = np.ones((n,1)) for k in range(maxCycles): h = sigmoid(dataMatrix*weights) error = labelMat - h weights += alpha * dataMatrix.transpose() * error return weights def plotBestFit(weights): dataMat,labelMat = loadDataSet() dataArr = np.array(dataMat) n = np.shape(dataArr)[0] xcord1 = [];ycord1 = [] xcord2 = [];ycord2 = [] for i in range(n): if int(labelMat[i]) == 1: xcord1.append(dataArr[i,1]);ycord1.append(dataArr[i,2]) else: xcord2.append(dataArr[i,1]);ycord2.append(dataArr[i,2]) fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(xcord1,ycord1,s=30,c='red',marker='s') ax.scatter(xcord2,ycord2,s=30,c='green') x = np.arange(-3.0,3.0,0.1) y = (-weights[0] - weights[1]*x)/weights[2] ax.plot(x,y) plt.xlabel('X1');plt.ylabel('X2') plt.show() if __name__ == '__main__': dataMat,labelMat = loadDataSet() weights = gradAscent(dataMat,labelMat) plotBestFit(weights)
运行结果:
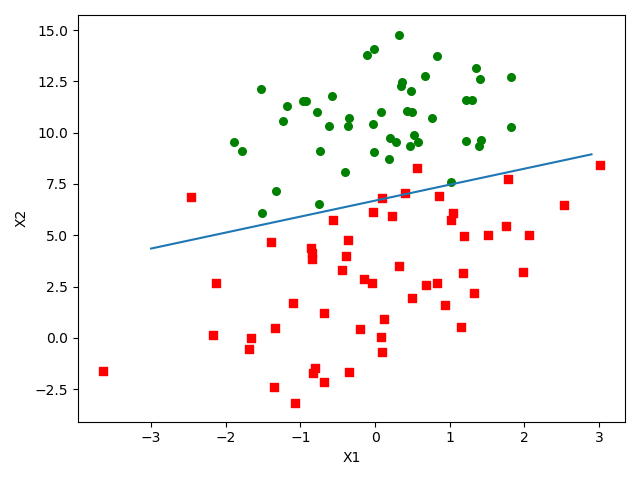
参考博客:https://cuijiahua.com/blog/2017/11/ml_6_logistic_1.html





 浙公网安备 33010602011771号
浙公网安备 33010602011771号